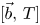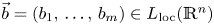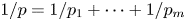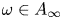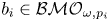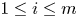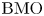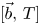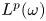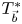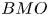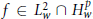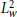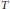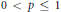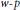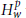4 results
The commutators of multilinear Calderón–Zygmund operators on weighted Hardy spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1259-1280
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
Square roots of weighted shifts of multiplicity two
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 23 December 2022, pp. 791-807
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Variational characterizations of weighted Hardy spaces and weighted $BMO$
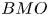 spaces
spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 01 December 2021, pp. 1613-1632
- Print publication:
- December 2022
-
- Article
- Export citation
Atomic Decomposition and Boundedness of Operators on Weighted Hardy Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 2 / 01 June 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 303-314
- Print publication:
- 01 June 2012
-
- Article
-
- You have access
- Export citation