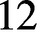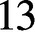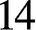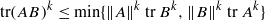Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
Contents
Maximal sum-free sets in finite abelian groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 289-297
-
- Article
-
- You have access
- Export citation
Maximal sum-free sets in finite abelian groups, II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 43-54
-
- Article
-
- You have access
- Export citation
Numbers of conjugacy classes in some finite classical groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 23-48
-
- Article
-
- You have access
- Export citation
THE AVERAGE DISTANCE BETWEEN TWO POINTS
- Part of:
-
- Published online by Cambridge University Press:
- 02 October 2009, pp. 353-359
-
- Article
-
- You have access
- Export citation
BLOCKS WITH SMALL-DIMENSIONAL BASIC ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2020, pp. 461-474
-
- Article
-
- You have access
- Open access
- Export citation
TRACE INEQUALITIES FOR MATRICES
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2012, pp. 139-148
-
- Article
-
- You have access
- Export citation
Convex lattice polygons of minimum area
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-367
-
- Article
-
- You have access
- Export citation
Conjugacy classes in projective and special linear groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 339-364
-
- Article
-
- You have access
- Export citation
Monochromatic triangles in three colours
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 197-212
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC PROPERTIES OF KOLMOGOROV WIDTHS
- Part of:
-
- Published online by Cambridge University Press:
- 25 March 2010, pp. 10-17
-
- Article
-
- You have access
- Export citation
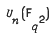 ;
; 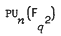 ,
, 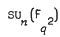 , and more generally
, and more generally 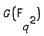 where
where 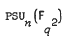 .
.