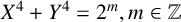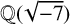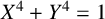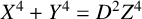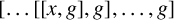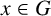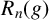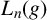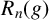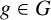Open access
Contents
Research Article
HALPHEN AND THE ELLIPTIC FUNCTIONS OF DU VAL
- Part of:
-
- Published online by Cambridge University Press:
- 12 December 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DERANGEMENTS IN PERMUTATION GROUPS WITH TWO ORBITS
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON SOME QUADRATICS AND CUBICS OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISED MAZUR’S GROWTH NUMBER CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUMS OF KLOOSTERMAN SUMS OVER SQUARE-FREE AND SMOOTH INTEGERS
- Part of:
-
- Published online by Cambridge University Press:
- 20 November 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE GENERALISED SQUEEZING FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 14 November 2025, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE LARGEST PRIME DIVISOR OF n! + 1
- Part of:
-
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE NUMBER OF PARTS IN A RANDOM t-REGULAR PARTITION
- Part of:
-
- Published online by Cambridge University Press:
- 16 October 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RUNS IN PAPERFOLDING SEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE FERMAT QUARTIC X4 + Y4 = 2m IN QUADRATIC NUMBER FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SEMIGROUP CONGRUENCES AND SUBSEMIGROUPS OF THE DIRECT SQUARE
- Part of:
-
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE LARGEST CHARACTER DEGREE OF SOLVABLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IMPROVED UPPER BOUND ON BRUN’S CONSTANT UNDER GRH
- Part of:
-
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGHT ENGEL CONDITIONS FOR ORDERABLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 27 June 2025, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ESWARATHASAN–LEVINE AND BOYD’S CONJECTURES FOR HARMONIC NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON IMPLICIT ITERATION PROCESSES
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
KRONECKER CLASSES, NORMAL COVERINGS AND CHIEF FACTORS OF GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A VERY SHORT PROOF OF SIDORENKO’S INEQUALITY FOR COUNTS OF HOMOMORPHISMS BETWEEN GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FORBIDDEN PARTITION CONFIGURATION SPACES OF GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2025, pp. 536-549
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ELEMENTARY PROOFS OF THE DIAMETER BOUNDS FOR POWER GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 11 February 2025, pp. 505-508
-
- Article
-
- You have access
- Open access
- HTML
- Export citation