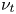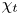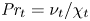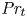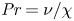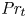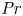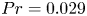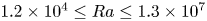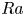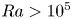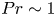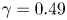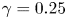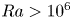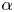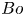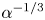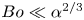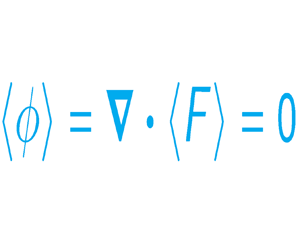JFM Rapids
Contents
JFM Rapids
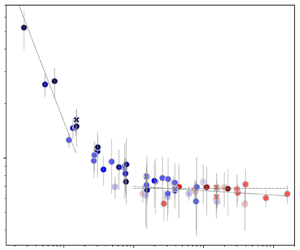
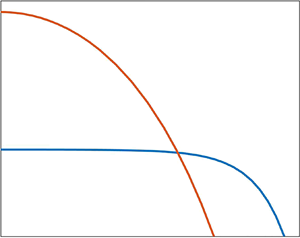
Turbulent Prandtl number from isotropically forced turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 952 / 2022
- Published online by Cambridge University Press:
- 22 November 2022, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weakly nonlinear evolution of stochastically driven non-normal systems
-
- Journal:
- Journal of Fluid Mechanics / Volume 951 / 2022
- Published online by Cambridge University Press:
- 14 November 2022, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tandem droplet locomotion in a uniform electric field
-
- Journal:
- Journal of Fluid Mechanics / Volume 951 / 2022
- Published online by Cambridge University Press:
- 10 November 2022, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flow states and heat transport in liquid metal convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 951 / 2022
- Published online by Cambridge University Press:
- 28 October 2022, R1
-
- Article
-
- You have access
- HTML
- Export citation
Shape of sessile drops at small contact angles
-
- Journal:
- Journal of Fluid Mechanics / Volume 950 / 2022
- Published online by Cambridge University Press:
- 26 October 2022, R4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Size-dependent transient nature of localized turbulence in transitional channel flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 950 / 2022
- Published online by Cambridge University Press:
- 26 October 2022, R3
-
- Article
- Export citation
The effect of particle anisotropy on the modulation of turbulent flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 950 / 2022
- Published online by Cambridge University Press:
- 24 October 2022, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vortex patterns in rapidly rotating Rayleigh–Bénard convection under spatial periodic forcing
-
- Journal:
- Journal of Fluid Mechanics / Volume 950 / 2022
- Published online by Cambridge University Press:
- 13 October 2022, R1
-
- Article
-
- You have access
- HTML
- Export citation
Direct statistical simulation of the Busse annulus
-
- Journal:
- Journal of Fluid Mechanics / Volume 949 / 2022
- Published online by Cambridge University Press:
- 03 October 2022, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Only two Betchov homogeneity constraints exist for isotropic turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 948 / 2022
- Published online by Cambridge University Press:
- 20 September 2022, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Added mass and damping of structures with periodic angular shape
-
- Journal:
- Journal of Fluid Mechanics / Volume 948 / 2022
- Published online by Cambridge University Press:
- 07 September 2022, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Assimilation of wall-pressure measurements in high-speed flow over a cone
-
- Journal:
- Journal of Fluid Mechanics / Volume 947 / 2022
- Published online by Cambridge University Press:
- 31 August 2022, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Low-order moments of the velocity gradient in homogeneous compressible turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 947 / 2022
- Published online by Cambridge University Press:
- 30 August 2022, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Synchronization of detonations: Arnold tongues and devil's staircases
-
- Journal:
- Journal of Fluid Mechanics / Volume 946 / 2022
- Published online by Cambridge University Press:
- 28 July 2022, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The streaks of wall-bounded turbulence need not be long
-
- Journal:
- Journal of Fluid Mechanics / Volume 945 / 2022
- Published online by Cambridge University Press:
- 22 July 2022, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Destabilization of binary mixing layer in supercritical conditions
-
- Journal:
- Journal of Fluid Mechanics / Volume 945 / 2022
- Published online by Cambridge University Press:
- 21 July 2022, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Soft streaming – flow rectification via elastic boundaries
-
- Journal:
- Journal of Fluid Mechanics / Volume 945 / 2022
- Published online by Cambridge University Press:
- 14 July 2022, R1
-
- Article
- Export citation
Stratified turbulent mixing in oscillating shear flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 944 / 2022
- Published online by Cambridge University Press:
- 06 July 2022, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Emergent rheotaxis of shape-changing swimmers in Poiseuille flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 944 / 2022
- Published online by Cambridge University Press:
- 24 June 2022, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pressure modes of the oscillating sessile drop
-
- Journal:
- Journal of Fluid Mechanics / Volume 944 / 2022
- Published online by Cambridge University Press:
- 22 June 2022, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation