In systems where the standard $\alpha$ effect is inoperative, one often explains the existence of mean magnetic fields by invoking the ‘incoherent $\alpha$ effect’, which appeals to fluctuations of the mean kinetic helicity at a mesoscale. Most previous studies, while considering fluctuations in the mean kinetic helicity, treated the mean turbulent kinetic energy at the mesoscale as a constant, despite the fact that both these quantities involve second-order velocity correlations. The mean turbulent kinetic energy affects the mean magnetic field through both turbulent diffusion and turbulent diamagnetism. In this work, we use a double-averaging procedure to analytically show that fluctuations of the mean turbulent kinetic energy at the mesoscale (giving rise to $\eta$-fluctuations at the mesoscale, where the scalar $\eta$ is the turbulent diffusivity) can lead to the growth of a large-scale magnetic field even when the kinetic helicity is zero pointwise. Constraints on the operation of such a dynamo are expressed in terms of dynamo numbers that depend on the correlation length, correlation time and strength of these fluctuations. In the white-noise limit, we find that these fluctuations reduce the overall turbulent diffusion, while also contributing a drift term which does not affect the growth of the field. We also study the effects of non-zero correlation time and anisotropy. Turbulent diamagnetism, which arises due to inhomogeneities in the turbulent kinetic energy, leads to growing mean-field solutions even when the $\eta$-fluctuations are statistically isotropic.

The well-known quadratic temperature–velocity (TV) relation is significant for physical understanding and modelling of compressible wall-bounded turbulence. Meanwhile, there is an increasing interest in employing the TV relation for laminar modelling. In this work, we revisit the TV relation for both laminar and turbulent flows, aiming to explain the success of the TV relation where it works, improve its accuracy where it deviates and relax its limitation as a wall model for accurate temperature prediction. We show that the general recovery factor defined by Zhang et al. (J. Fluid. Mech., vol. 739, 2014, pp. 392–440) is not a wall-normal constant in most laminar and turbulent cases. The effective Prandtl number $Pr_e$ is more critical in determining the shape of temperature profiles. The quadratic TV relation systematically deviates for laminar boundary layers irrespective of Mach number and wall boundary conditions. We find a universal distribution of 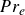$Pr_e$, based on which the TV relation can be notably improved, especially for cold-wall cases. For turbulent flows, the TV relation as the wall model can effectively improve the near-wall temperature prediction for cold-wall boundary layer cases, but it involves boundary-layer-edge quantities used in the Reynolds analogy scaling, which hinders the application of the wall model in complex flows. We propose a transformation-based temperature wall model by solving inversely the newly developed temperature transformation of Cheng and Fu (Phy. Rev. Fluids, vol. 9, 2024, no. 054610). The dependence on edge quantities is thus removed in the new model and the high accuracy in turbulent temperature prediction is maintained for boundary layer flows.

We study the dynamics of an initially axisymmetric and vertical Lamb–Oseen vortex in a stratified-rotating fluid under the complete Coriolis force on the $f$ plane, i.e. in the presence of a background rotation both along the vertical and horizontal directions. By a combination of direct numerical simulations and asymptotic analyses for small horizontal background rotation, we show that a critical layer appears at the radius where the angular velocity of the vortex is equal to the buoyancy frequency when the Froude number is larger than unity. This critical layer generates a vertical velocity that is invariant along the vertical and which first increases linearly with time and then saturates at an amplitude scaling like $Re^{1/3}/\widetilde{Ro}$, where $Re$ is the Reynolds number and $\widetilde {Ro}$ the non-traditional Rossby number based on the horizontal component of the background rotation. In turn, a quasi-axisymmetric anomaly of vertical vorticity is produced at the critical radius through the non-traditional Coriolis force. Below a critical $\widetilde {Ro}$ depending on $Re$, the Rayleigh's inflectional criterion is satisfied and a shear instability is subsequently triggered rendering the vertical vorticity fully non-axisymmetric. The decay of the angular velocity is then enhanced until it is everywhere lower than the buoyancy frequency. A theoretical criterion derived from the Rayleigh condition predicts well the instability. It shows that this phenomenon can occur even for a large non-traditional Rossby number $\widetilde {Ro}$ for large $Re$. Hence, the non-traditional Coriolis force might have much more impact on geophysical vortices than anticipated by considering the order of magnitude of $\widetilde {Ro}$.

An efficient numerical method for calculation of the sea surface skewness and kurtosis for arbitrary wave spectra, taking up to third-order nonlinear effects into account, is developed. The skewness and kurtosis are calculated for a large number of sea states, covering a wide range of sea-state parameters in terms of wave steepness, water depth, directional spreading and frequency bandwidth. The results are used to propose new accurate expressions for skewness and kurtosis, valid over a wide range of sea states. Existing expressions for skewness and kurtosis reported in the literature are reviewed, and their accuracy is evaluated. Comparison to model-test results and phase-resolved numerical simulation are presented. It is suggested that the new improved parametrizations for skewness and kurtosis, which include dependence on wave steepness, water depth, spectral bandwidth and directional spreading, represent a convenient way to include these covariates into higher-order distributions for crest heights, wave heights and surface elevation.

Analysis of the classic problem of shallow film flow on an inclined plane is revisited for a Brownian suspension. The particle phase, considered in a two-fluid model, is predicted to cause pronounced changes to the instability characteristics of the flow. These are due to an indirect effect of the non-Newtonian rheology, with the normal stresses causing migration and a viscosity stratification which strongly alters the base state from its Newtonian counterpart. Both the short- and long-wavelength inertial stability boundaries are altered, and, more strikingly, an instability at zero Reynolds number is found.

A moving static pressure distribution is commonly used to simulate a travelling ship. However, the ship movement changes the fluid velocity around the hull, inducing pressures on the hull surface that are no longer equal to the static pressure. Therefore, we introduce a dynamic pressure correction strategy, which can accurately simulate the impact of the ship movement on the hull-surface pressure and preserve the desired hull shape under both stationary and transient conditions. The strategy is applied to a high-order spectral model and used to investigate ship-induced waves and wave resistance over a both flat and variable topography. We explore various parameters in our study, including the average water depth to ship draft ratio ($h_0/d$), the channel width to ship width ratio ($W/B$), the Froude number ($Fr_0=U/\sqrt {gh_0}$) and variations in bathymetric slope. Compared with experiments on a flat bottom, the numerical results with dynamic correction show better accuracy in the simulation of ship-induced waves and wave resistance than those obtained using a static pressure distribution. The correlation coefficient for wake waves between the numerical and experimental results is improved by approximately 0.25 with the dynamic correction strategy. The amplitude and wavelength of ship-induced mini-tsunamis over a variable topography are found to be reduced when employing a dynamic correction compared with a static pressure distribution, and this effect becomes more pronounced with higher Froude number. The static pressure approach is shown to allow large deformations of the desired hull shape and changes in ship volume which are responsible for the different wave patterns from the two approaches.

The pseudo-incompressible approximation, which assumes small pressure perturbations from a one-dimensional reference state, has long been used to model large-scale dynamics in stellar and planetary atmospheres. However, existing implementations do not conserve energy when the reference state is time-dependent. We use a variational formulation to derive an energy-conserving pseudo-incompressible model in which the reference state evolves while remaining hydrostatic. We present an algorithm for solving these equations in the case of closed boundaries, for which the pseudo-incompressible velocity constraint is degenerate. We implement the model within the low-Mach-number code MAESTROeX, and validate it against a fully compressible model in several test cases, finding that our hybrid pseudo-incompressible–hydrostatic model generally shows better agreement with the compressible results than the existing MAESTROeX implementation.

A linear stability analysis of circular Couette flow of a Bingham fluid subjected to axisymmetric perturbations was presented by Peng & Zhu (J. Fluid Mech., vol. 512, 2004, pp. 21–45) and Landry et al. (J. Fluid Mech., vol. 560, 2006, pp. 321–353). Here, we consider the stability of this flow with respect to a finite amplitude perturbation. We focus particularly on the case where the basic flow has an unyielded fluid layer on outer cylinder. A weakly nonlinear stability analysis is developed for a wide gap and a narrow gap. A third-order Ginzburg–Landau equation is derived, and the influence of the different nonlinearities on bifurcation features is investigated in detail. The results indicate that: (i) the nonlinear inertial terms act in favour of pitchfork supercritical bifurcation and the nonlinear yield stress terms promote a subcritical bifurcation; (ii) for a range of Bingham numbers $B$, the extent of which depends on the radius ratio and outer Reynolds number, the nonlinear yield stress terms are dominant and the primary bifurcation is subcritical. The amplitude analysis indicates that in the supercritical bifurcation regime, near the threshold, when the nonlinear inertial terms are dominant, the amplitude decreases slightly with increasing $B$. Once the nonlinear yield stress terms start to become significant, the equilibrium amplitude increases substantially with increasing $B$. Similar trends are observed for Taylor vortex strength. Finally, the erosion of the static layer is analysed. It is shown that the nonlinear yield stress terms play a significant role.

The orientational dynamics of a spherical magnetic particle in linear shear flow subjected to an oscillating magnetic field in the flow plane is analysed in the viscous limit. The shear is in the $X$–$Y$ plane, the magnetic field is in the $X$ direction and the vorticity is perpendicular to the flow in the $Z$ direction. The relevant dimensionless groups are $\omega ^\ast$, the ratio of the frequency of the magnetic field and the strain rate, and $\varSigma$, the ratio of the magnetic and hydrodynamic torques. As $\varSigma$ is decreased, there is a transition from in-plane rotation, where the rotation is in the flow ($X$–$Y$) plane, to out-of-plane rotation, where the orientation vector is not necessarily in the $X$–$Y$ plane and the dynamics depends on the initial orientation. The particle rotation is phase-locked for in-plane rotation with discrete odd rotation number (number of rotations in one period of magnetic field oscillation), while the orbits are quasi-periodic with non-integer rotation number for out-of-plane rotation. For $\varSigma \gg 1$, regions of odd rotation number $n_o$ are bound by the lines $8 (n_o-1) \varSigma \omega ^\ast = 1$ and $8 (n_o+1) \varSigma \omega ^\ast = 1$, and there are discontinuous changes in the rotation number and mean and root-mean-square torque at these lines. For $\varSigma \ll 1$, the domains of in-plane rotation of finite width in the $\omega ^\ast$–$\varSigma$ plane extend into downward cusps at $\omega ^\ast = {1}/{2 n_o}$. The orbits are quasi-periodic between these domains, where the rotation is out of plane.

We investigate the concentration fluctuations of passive scalar plumes emitted from small, localised (point-like) steady sources in a neutrally stratified turbulent boundary layer over a rough wall. The study utilises high-resolution large-eddy simulations for sources of varying sizes and heights. The numerical results, which show good agreement with wind-tunnel studies, are used to estimate statistical indicators of the concentration field, including spectra and moments up to the fourth order. These allow us to elucidate the mechanisms responsible for the production, transport and dissipation of concentration fluctuations, with a focus on the very near field, where the skewness is found to have negative values – an aspect not previously highlighted. The gamma probability density function is confirmed to be a robust model for the one-point concentration at sufficiently large distances from the source. However, for ground-level releases in a well-defined area around the plume centreline, the Gaussian distribution is found to be a better statistical model. As recently demonstrated by laboratory results, for elevated releases, the peak and shape of the pre-multiplied scalar spectra are confirmed to be independent of the crosswind location for a given downwind distance. Using a stochastic model and theoretical arguments, we demonstrate that this is due to the concentration spectra being directly shaped by the transverse and vertical velocity components governing the meandering of the plume. Finally, we investigate the intermittency factor, i.e. the probability of non-zero concentration, and analyse its variability depending on the thresholds adopted for its definition.

We study the statistical properties of scalar fields undergoing reversible chemical reactions in a turbulent environment by means of numerical simulations. To produce strong chemical fluctuations in a wide region of the domain, an original flow configuration has been proposed, where the species are supplied from buffer boundaries with adjustable thickness, while the flow is developed homogeneous and isotropic turbulence in a periodic domain. With the presence of the mean scalar gradient in the bulk region, the strength of turbulent advection is comparable with the chemical source, which is quantified by the Damköhler number. Our analysis focuses on the global and spatial properties of the reactive scalars in their statistically steady regime. We show how for the case of a second-order reaction such features can be connected to the properties of a non-reactive scalar field advected in the same system. Analytical predictions of the scalar moments in the fast reaction regime agree satisfactorily with the direct numerical simulation results. In comparison with the existing results of the isotropic turbulence case, we conclude that the scalar correlation is jointly determined by both the chemical source and the flow configuration. Moreover, the chemical reaction also plays an important role in determining the scalar energy spectra.