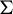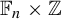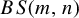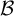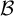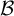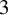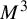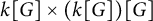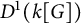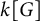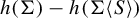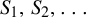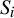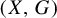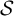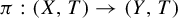Refine listing
Actions for selected content:
300 results in 37Bxx
Tame or wild Toeplitz shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 1379-1417
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Encoding subshifts through sliding block codes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1609-1628
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orbits closeness for slowly mixing dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1192-1208
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuum of allosteric actions for non-amenable surface groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 19 July 2023, pp. 1581-1596
- Print publication:
- June 2024
-
- Article
- Export citation
On the abundance of k-fold semi-monotone minimal sets in bimodal circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 12 July 2023, pp. 1269-1314
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Word complexity of (measure-theoretically) weakly mixing rank-one subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 1330-1366
- Print publication:
- May 2024
-
- Article
- Export citation
Strongly aperiodic SFTs on generalized Baumslag–Solitar groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 20 June 2023, pp. 1209-1238
- Print publication:
- May 2024
-
- Article
- Export citation
Automorphisms of
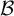 ${\mathcal B}$-free and other Toeplitz shifts
${\mathcal B}$-free and other Toeplitz shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 1058-1101
- Print publication:
- April 2024
-
- Article
- Export citation
A word of low complexity without uniform frequencies
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1013-1025
- Print publication:
- April 2024
-
- Article
- Export citation
Cancellations of periodic orbits for non-singular Morse–Smale flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 25 May 2023, pp. 1123-1171
- Print publication:
- April 2024
-
- Article
- Export citation
Counting independent sets in amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 May 2023, pp. 958-1012
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable finiteness of twisted group rings and noisy linear cellular automata
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1089-1108
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Proper extensions of the 2-sphere’s conformal group present entropy and are 4-transitive
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 03 May 2023, pp. 1102-1122
- Print publication:
- April 2024
-
- Article
- Export citation
Binary factors of shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 18 April 2023, pp. 888-932
- Print publication:
- March 2024
-
- Article
- Export citation
Entropy bounds for multi-word perturbations of subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 665-673
- Print publication:
- February 2024
-
- Article
- Export citation
Relative uniformly positive entropy of induced amenable group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 17 March 2023, pp. 569-593
- Print publication:
- February 2024
-
- Article
- Export citation
Dynamical properties of minimal Ferenczi subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 22 February 2023, pp. 3923-3970
- Print publication:
- December 2023
-
- Article
- Export citation
Sequence entropy tuples and mean sensitive tuples
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 20 February 2023, pp. 184-203
- Print publication:
- January 2024
-
- Article
- Export citation
Almost proximal extensions of minimal flows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 16 January 2023, pp. 4041-4073
- Print publication:
- December 2023
-
- Article
- Export citation
Recognizability of morphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 3578-3602
- Print publication:
- November 2023
-
- Article
- Export citation