When multiple operators are connected to a single power source which is not large enough to simultaneously supply all users, interference can take place. This paper considers two models of a spot welding station which differ in the method of resolving interference between users. In the first model the system is allowed to become overloaded and the consequent deterioration in weld quality is accepted. In the second model any request which will overload the system is rejected. Expressions are found for (a) the proportion of poor quality welds in the first model and (b) the probability of operators being rejected in the second model. Numerical results are given which indicate how small the power supply can be made for a typical welding shop while keeping interference at a minimal level.

The reflection-transmission properties of water waves obliquely incident upon a vortex sheet in water of finite depth are studied. The problem is reduced to that of solving two integral equation. An accurate Galerkin solution is obtained which supports the use of the “variational method” in water wave problems that has recently been questioned by Kirby and Dalyrmple.

The unsteady Hele-Shaw problem is a model nonlinear system that, for a certain parameter ranger, exhibits the phenomenon known as viscous fingering. While not directly applicable to multiphase porous-media flow, it does prove to be an adequate mathematical model for unstable dieplacement in laboratory parallel-plate devices. We seek here to determine, by use of an accurate boundary-integral frount-tracking scheme, the extent to which the simplified system captures the canonical nonlinear behavior of displacement flows and, in particular, to ascertain the role of noise in such systems. We choose to study a particular pattern of injection and production “wells.” The pattern chosen is the isolated “five-spot,” that is a single source surrounded by four symmetrically-placed sinks in an infinite two-dimensional “reservoir.” In cases where the “pusher” fluid has negligible viscosity, sweep efficiency is calculated for a range of values of the single dimensionless parameter τ, an inverse capillary number. As this parameter is reduced, corresponding to increased flow rate or reduced interfacial tension, this efficiency decreases continuously. For small values of τ, these stable displacements change abruptly to a regime characterized by unstable competing fingers and a significant reduction in sweep efficiency. A simple stability argument appears to correctly predict the noise level required to transit from the stable to the competing-finger regimes. Published compilations of experimental results for sweep efficiency as a function of viscosity ratio showed an unexplained divergence when the pusher fluid is less viscous. Our simulations produce a similar divergence when, for a given viscosity ratio, the parameter τ is varied.

Mathematical theories describing chaotic behaviour in physical systems are introduced by developing and reviewing applications to optical fibres. A theory is presented for laser light propagating in a loop formed by an optical fibre and an optical coupler. As the light traverses the fibre it suffers an attenuation and is subjected to a phase shift which will have a component proportional to the light intensity via the nonlinear optics Kerr effect. At each pass through the coupler, an extra fraction of laser light is coupled into the loop. The mathematical formulation leads to a two-dimensional map having a clear physical and geometrical interpretation. The complete solution is given in the linear regime and the onset of nonlinear behaviour is investigated as the laser power is increased. A variety of transitions is obtained including period doubling and iteration onto a strange attractor.

The problem of a source or sink submerged beneath a free surface is investigated in the infinite Froude number limit. Solutions are found for all cases in which the source is situated away from the bottom of the channel. Solutions are also found for the case where the source is situated above the asymptotic level of the free surface, giving fountain type free surface shapes.

This note generalises the necessary and sufficient conditions for one act to be dominated by another when the two acts available to the decision maker have outcomes contingent on discrete states of nature whose probabilities of occurrence are known only to the extent of linear partial information. The generalisation relates to the dominance of an act by a set of acts. The presentation is in terms of general vector dominance, of which statistical dominance is only a particular case.

The method of matched asymptotic expanisions is used to solve the problem of flow over a thin airfoil possessing a trailing-edge appendage, which may be of a general character, but is confined to a region of small size compated to the airfoil' chord. A feature of this asymptotic solution is effective de-coupling of the flow problems for the main airfoil and the flap. The special case of an attached flat flap set at an arbitrary angle is solved in detail.

“Steady state” periodic solutions are sought to the forced Duffing equation. The solutions are expressed as formal Fourier series, giving rise to an infinite system of non-linear algebraic equations for the Fourier coefficients. This system is then solved using perturbation series in the amplitude of the forcing term. Solution profiles of high accuracy and phase-plane orbits are presented. The existence of limiting values of the forcing amplitude is discussed, and points of non-linear resonance are identified.

The modulation of short gravity waves by long waves or currents is described for the situation when the flow is irrotational and when the short waves are described by linearised equations. Two cases are distinguished depending on whether the basic flow can be characterised as a deep-water current, or a shallow-water current. In both cases the basic flow has a current which has finite amplitude, while in the first case the free surface slope of the basic flow can be finite, but in the second case is small. The modulation equations are the local dispersion relation of the short waves, the kinematic equation for conservation of wave crests and the wave action equation. The results incorporate and extend the earlier work of Longuet-Higgins and Stewart [10, 11].

It is shown that barrier functions applied to the dual linear program can be modified to give multiplier estimates that converge to the solution of the primal problem. Newton's method is considered for implementing this approach and numerical results presented. It has been shown that there is a connection between these methods and Karmarkar's algorithm, but for the class of problems considered further improvements are still required before those methods become competitive with active set methods.

From a knowledge of the eigenvalue spectrum of the Laplacian on a domain, one may extract information on the geometry and boundary conditions by analysing the asymptotic expansion of a spectral function. Explicit calculations are performed for isosceles right-angle triangles with Dirichlet or Neumann boundary conditions, yielding in particular the corner angle terms. In three dimensions, right prisms are dealt with, including the solid vertex terms.

A model is developed for the seif-organisation of zones of enzymatic activity along a liver capillary (hepatic sinusoid) lined with cells of two types, which contain different enzymes and compete for sites on the wall of the sinusoid. An effectively non-local interaction between the cells arises from local consumption of oxygen from blood flowing throug1 the sinusoid, which gives rise to gradients of oxygen concentration in turn influencing rates of division and of death of the two cell-types. The process is modelled by a pair of coupled non-linear integro-differential equations for the cell-densities as functions of time and position along the sinusoid. Existence of a unique, bounded, non-negative solution of the equations is proved, for prescribed initial values. The equations admit infinitely many stationary solutions, but it is shown that all except one are unstable, for any given set of the model parameters. The remaining solution is shown to be asymptotically stable against a large class of perturbations. For certain ranges of the model parameters, the asymptotically stable stationaxy solution has a zonal structure, with cells of one type located entirely upstream of cells of the other type, and with jump discontinuities in the cell densities at a certain distance along the sinusoid. Such sinusoidal zones can account for zones of enzymatic activity observed in the intact liver. Exceptional cases are found for singular choices of model parameters, such that stationary cell-densities cannot be asymptotically stable individually, but together form an asymptotically stable set. Certain mathematical questions are left open, notably the behaviour of large deviations from stationary solutions, and the global stability of such solutions. Possible generalisations of the model are described.

Conditions are fround for the convergence of intepolatory product integration rules and the corresponding companion rules for the class of Riemann-integrable functions. These condtions are used to prove convergence for several classes of rules based on sets of zeros of orthogonal polynomials possibly augmented by one both of the endpoints of the integration interval.

The leading-order interaction of short gravity waves with a dominant long-wave swell is calculated by means of Zakharov's [7] spectral formulation. Results are obtained both for a discrete train of short waves and for a localised wave packet comprising a spectrum of short waves.

The results for a discrete wavetrain agree with previous work of Longuet-Higgins & Stewart [5], and general agreement is found with parallel work of Grimshaw [4] which employed a very different wave-action approach.

An investigation is made of a hybrid method inspired by Riccati transformations and marching algorithms employing (parts of) orthogonal matrices, both being decoupling algorithms. It is shown that this so-called continuous orthonormalisation is stable and practical as well. Nevertheless, if the problem is stiff and many output points are required the method does not give much gain over, say, multiple shooting.

It is well known that n-process, n-commodity (or square), models of productive single-product industries have positive solutions to their price and quantity systems if the rates of profit and growth lie in appropriate non-negative intervals. On the other hand, negative prices and quantities can occur in formal solutions of models of square, productive, multiple-product industries even when the rates of profit and growth are less than their respective maximum positive values. It is shown in this paper that these differences can be attributed to the presence in joint production of dominance, in either row or column versions. Results on positive solutions to the price (respectively, quantity) system are derived in terms of the absence of column (respectively, row) dominance of the net output matrix. As the concepts of row and column dominance are defined in terms of linear inequalities, the basic mathematical results to be applied are theorems of the alternative.

Algorithms are developed by means of which certain connected pairs of Fredholm integral equations of the first and second kinds can be converted into Fredholm integral equations of the second kind. The methods are then used to obtain the solutions of two different sets of triple integral equations tht occur in mixed boundary value problems involving Laplace' equation and the wave equation respectively.

This paper studies the impairing of flows in multi-index transportation problem with axial constraints. For any curtailed flow, the problem is shown to be equivalent to a standard axial sum problem, whose solution can be obtained by known methods. The equivalence is established only for specially defined solutions (referred to as M-feasible solutions) of the standard problem. It is also proved that an optimal solution of the impaired flow problem corresponds to such an M-feasible solution.

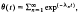The spectral function , where 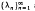are the eigenvalues of the two-dimensional Laplacian, is studied for a variety of domains. The dependence of θ(t) on the connectivity of a domain and the impedance boundary conditions is analysed. Particular attention is given to a doubly-connected region together with the impedance boundary conditions on its boundaries.

A quasi-steady-state apprcncimation to the Navier-Stokes equation is the corresponding equation with nonhomogeneous forcing term f(x, t), but with the term Vt deleted. For solutions that are zero on the boundary, the difference z between the solution of the Navier-Stokes equation and the solution of this quasi-steady-state approximation is estimated in the L2 norm ║z║ with respect to the spatial variables. For sufficiently large viscosity or sufficiently small body force f, the inequality

holds for 0 < t ≤ T and certain real numbres C, β > 0.