Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ALLEN, ROBERT F.
and
COLONNA, FLAVIA
2009.
ISOMETRIES AND SPECTRA OF MULTIPLICATION OPERATORS ON THE BLOCH SPACE.
Bulletin of the Australian Mathematical Society,
Vol. 79,
Issue. 1,
p.
147.
Hedayatian, Karim
Karimi, Lotfollah
and
Stević, Stevo
2009.
On Convexity of Composition and Multiplication Operators on Weighted Hardy Spaces.
Abstract and Applied Analysis,
Vol. 2009,
Issue. 1,
Allen, Robert F.
and
Colonna, Flavia
2009.
On the isometric composition operators on the Bloch space in Cn.
Journal of Mathematical Analysis and Applications,
Vol. 355,
Issue. 2,
p.
675.
Akeroyd, John R.
Ghatage, Pratibha G.
and
Tjani, Maria
2010.
Closed-Range Composition Operators on $${\mathbb{A}^2}$$ and the Bloch Space.
Integral Equations and Operator Theory,
Vol. 68,
Issue. 4,
p.
503.
Laitila, Jussi
2010.
Isometric composition operators on BMOA.
Mathematische Nachrichten,
Vol. 283,
Issue. 11,
p.
1646.
Allen, Robert F.
and
Colonna, Flavia
2010.
Topics in Operator Theory.
p.
11.
Martín, María J.
2010.
Norm-attaining composition operators on the Bloch spaces.
Journal of Mathematical Analysis and Applications,
Vol. 369,
Issue. 1,
p.
15.
Allen, Robert F.
and
Colonna, Flavia
2010.
Weighted Composition Operators from H ∞ to the Bloch Space of a Bounded Homogeneous Domain.
Integral Equations and Operator Theory,
Vol. 66,
Issue. 1,
p.
21.
Li-Gang Geng
and
Ce-Zhong Tong
2011.
Some isometric operators on the Dirichlet space.
p.
6544.
Zorboska, Nina
and
Arai, Asao
2011.
Isometric and Closed‐Range Composition Operators between Bloch‐Type Spaces.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2011,
Issue. 1,
Li, Songxiao
2012.
Differences of generalized composition operators on the Bloch space.
Journal of Mathematical Analysis and Applications,
Vol. 394,
Issue. 2,
p.
706.
Zorboska, Nina
2012.
Univalently Induced, Closed Range, Composition Operators on the Bloch-type Spaces.
Canadian Mathematical Bulletin,
Vol. 55,
Issue. 2,
p.
441.
Geng, Li-Gang
Zhou, Ze-Hua
and
Dong, Xing-Tang
2012.
Isometric composition operators on weighted Dirichlet-type spaces.
Journal of Inequalities and Applications,
Vol. 2012,
Issue. 1,
Zorboska, Nina
2013.
Fredholm and Semi-Fredholm Composition Operators on the Small Bloch-type Spaces.
Integral Equations and Operator Theory,
Vol. 75,
Issue. 4,
p.
559.
Allen, Robert F.
Heller, Katherine C.
and
Pons, Matthew A.
2014.
Isometric composition operators on the analytic Besov spaces.
Journal of Mathematical Analysis and Applications,
Vol. 414,
Issue. 1,
p.
414.
Sehba, Benoît
and
Stević, Stevo
2014.
On some product-type operators from Hardy–Orlicz and Bergman–Orlicz spaces to weighted-type spaces.
Applied Mathematics and Computation,
Vol. 233,
Issue. ,
p.
565.
Shabazz, Melissa
and
Tjani, Maria
2016.
Isometries among composition operators on Besov type spaces.
Complex Variables and Elliptic Equations,
Vol. 61,
Issue. 6,
p.
761.
Colonna, Flavia
and
Hmidouch, Nacir
2019.
Weighted Composition Operators on Iterated Weighted-Type Banach Spaces of Analytic Functions.
Complex Analysis and Operator Theory,
Vol. 13,
Issue. 4,
p.
1989.
Jiménez-Vargas, A.
2020.
Isometric Composition Operators on Lipschitz Spaces.
Mediterranean Journal of Mathematics,
Vol. 17,
Issue. 2,
Aljuaid, Munirah
and
Colonna, Flavia
2020.
Composition Operators on Some Banach Spaces of Harmonic Mappings.
Journal of Function Spaces,
Vol. 2020,
Issue. ,
p.
1.

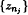 satisfying the conditions
satisfying the conditions 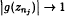 , and
, and