Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T05:19:44.486Z Has data issue: false hasContentIssue false
  • English
  • Français

Usco selections of densely defined set-valued mappings

Published online by Cambridge University Press:  17 April 2009

Warren B. Moors  and
Sivajah Somasundaram
Warren B. Moors
Affiliation:
Department of Mathematics, The University of Waikato, Private Bag 3105, Hamilton, New Zealand e-mail: moors@math.waikato.ac.nz, ss15@math.waikato.ac.nz
Sivajah Somasundaram
Affiliation:
Department of Mathematics, The University of Waikato, Private Bag 3105, Hamilton, New Zealand e-mail: moors@math.waikato.ac.nz, ss15@math.waikato.ac.nz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A set-valued mapping Φ : X → 2Y acting between topological spaces X and Y is said to be “lower demicontinuous” if the interior of the closure of the set Φ−1(V): = {x ∈ X : Φ(x) ∩ V ≠ ∅} is dense in the closure of Φ−1(V) for each open set V in Y. Čoban, Kenderov and Revalski (1994) showed that for every densely defined lower demicontinuous mapping Φ acting from a Baire space X into subsets of a monotonely Čech-complete space Y, there exist a dense and Gδ subset X1 ⊆ X and an usco mapping G: X1 → 2Y such that G (x) ⊆ Φ*(x), for every x ∈ X1, where the mapping Φ*: X → 2Y is the extension of Φ defined by,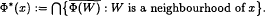 W is a neighbourhood of x}.

In this paper we present a proof of the above result with the notion of monotone Čcech-completeness replaced by the weaker notion of partition completeness. In addition, we observe that if the range space also lies is Stegall's class then we may assume that the mapping G is single-valued on X1.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 65 , Issue 2 , April 2002 , pp. 307 - 313
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Borwein, J.M. and Moors, W.B., ‘Essentially smooth Lipschitz function’, J. Funct. Anal. 149 (1997), 305–351.Google Scholar
[2]Christensen, J.P.R., ‘Theorems of Namioka and R.R. Johnson type for upper semicontinuous and compact valued set-valued mapping’, Proc. Amer. Math. Soc. 86 (1982), 649–655.Google Scholar
[3]Čoban, M.M., Kenderov, P.S. and Revalski, J.P., ‘Densely defined selections of multivalued mapping’, Trans. Amer. Math. Soc. 344 (1994), 203–223.Google Scholar
[4]Giles, J.R. and Moors, W.B., ‘A selection theorem for quasi-lower semicontinuous set-valued mapping’, J. Nonlinear Convex Anal 2 (2001), 345–350.Google Scholar
[5]Micheal, E., ‘Almost complete spaces, hypercomplete spaces and related mapping theorems’. Topology Appl. 41 (1991), 113–130.CrossRefGoogle Scholar
[6]Oxtoby, J.C., Measure and category, Graduate Text in Maths. 2 (Springer-Verlag, New York, 1971).CrossRefGoogle Scholar