Let G be a finitely connected domain and let X be a reflexive Banach space of functions analytic on G which admits the multiplication Mz as a polynomially bounded operator. We give some conditions that a sequence in G has an interpolating subsequence for X.

Dedicated to Professor Koichi Ogiue on his sixtieth birthday

We show that the only parallel surfaces in SL (2,ℝ) are rotational surfaces with constant mean curvature.

Let  be a Banach algebra and let ** be the second dual algebra of  endowed with the first or the second Arens product. We investigate relations between amenability of ** and Arens regularity of  and the rôle topological centres in amenability of **. We also find conditions under which weak amenability of ** implies weak amenability of .

In this paper, for a given Fuchsian group Γ, we prove an upper estimate for the Hausdorff dimension of the radial limit set in the visibility manifold. Further, if Γ is a convex cocompact group, we find the exact Hausdroff dimension of the limit set.

Order components of a finite group are introduced in [4]. We prove that, for every q, PSL (5,q) can be uniquely determined by its order componets. A main consequence of our result is the validity of Thompson's conjecture for the groups under consideration.

Two smoothness characterisations of weakly compact sets in Banach spaces are given. One that involves pointwise lower semicontinuous norms and one that involves projectional resolutions of identity.

We prove an explicit Hecke's bound for the Fourier coefficients of holomorphic cusp forms for SL2(Z) and apply it to derive effectively computable constants c (m) for each dimension m, divisible by 8, for which every even integer is always represented by every even unimodular form of m variables.

We study homomorphisms form the ring of Siegel modular forms of a given degree to the ring of elliptic modular forms for a congruence subgroup. These homomorphisms essentially arise from the restriction of Siegel modular forms to modular curves. These homomorphisms give rise to linear relations among the Fourier coefficients of a Siegel modular form. We use this technique to prove that dim .

Dedicated to Professor Kôzô Yabuta on the occasion of his 60th birthday

J. Kinnunen proved that of P > 1, d ≤ 1 and f is a function in the Sobolev space W1,P(Rd), then the first order weak partial derivatives of the Hardy-Littlewood maximal function ℳf belong to LP(Rd). We shall show that, when d = 1, Kinnunen's result can be extended to the case where P = 1.

For an even Dirichlet character ψ, we obtain a formula for L (1, ψ) in terms of a sum of Dirichlet L-Series evaluated at s = 2 and s = 3 and a rapidly convergent numerical series involving the central binomial coefficients. We then derive a class number formula for real quadratic number fields by taking L (s, ψ) to be the quadratic L-series associated with these fields.

We prove that there exists a soluble, saturated and s-closed formation ℱ of groups such that the class (Gℱ | G is a group, Gℱ is the ℱ-residual of G) is not closed under subdirect products. This result a negative answer to an open problems recently proposed by L.A. Shemetkov in 1998.

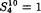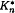Let G be a transitive permutation group acting on a finite set of order n. We discuss certain types of transversals for a point stabiliser A in G: free transversals and global transversals. We give sufficient conditions for the existence of such transversals, and show the connection between these transversals and combinatorial problems of decomposing the complete directed graph into edge disjoint cycles. In particular, we classify all the inner-transitive Oberwolfach factorisations of the complete directed graph. We mention also a connection to Frobenius theorem.

Under suitable assumptions we establish the formulas for calculating generalised gradients and generalised directional derivatives in the Clarke sense of the supremum and the infimum of an infinite family of Lipschitz functions. From these results we derive the results ensuring such a supremum or infimum are an invex function when all functions of the invex. Applying these results to a class of mathematical programs, we obtain necessary and sufficient conditions for optimality.

A set-valued mapping Φ : X → 2Y acting between topological spaces X and Y is said to be “lower demicontinuous” if the interior of the closure of the set Φ−1(V): = {x ∈ X : Φ(x) ∩ V ≠ ∅} is dense in the closure of Φ−1(V) for each open set V in Y. Čoban, Kenderov and Revalski (1994) showed that for every densely defined lower demicontinuous mapping Φ acting from a Baire space X into subsets of a monotonely Čech-complete space Y, there exist a dense and Gδ subset X1 ⊆ X and an usco mapping G: X1 → 2Y such that G (x) ⊆ Φ*(x), for every x ∈ X1, where the mapping Φ*: X → 2Y is the extension of Φ defined by, W is a neighbourhood of x}.

In this paper we present a proof of the above result with the notion of monotone Čcech-completeness replaced by the weaker notion of partition completeness. In addition, we observe that if the range space also lies is Stegall's class then we may assume that the mapping G is single-valued on X1.

This paper considers random fractals generated by contractive transformations which satisfy a separation condition weaker than the open set condition. This condition allows overlaps in the iterations. Estimates of the Hausdorff dimension of this kind of random fractals are obtained.

Steady waves at the free surface of an incompressible fluid passing over a depression are considered. By studying a KdV equation with negative forcing term, new types of solutions are discovered numerically and a new cut-off value of the Froude number, above which unsymmetric solitary-wave-like wave solutions exist, is also found.

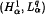In this note, we consider multipliers on weighted function spaces over totally disconnected locally compact Abelian groups (Vilenkin groups). First we present an multiplier result. Then we give an 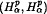multiplier result under a similar condition of Lu-Yang type. In Section 3, we obtain a result about the boundedness of multipliers on weighted Besov spaces.