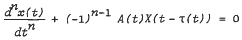Research Article
Metric spaces which cannot be isometrically embedded in Hilbert space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-167
-
- Article
-
- You have access
- Export citation
A note on the central limit theorem for geodesic random walks
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-173
-
- Article
-
- You have access
- Export citation
A remark on products of locally soluble groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 175-177
-
- Article
-
- You have access
- Export citation
Two-sided localization in semiprime FBN rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 179-191
-
- Article
-
- You have access
- Export citation
Generalized convexity in nondifferentiable programming
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 193-218
-
- Article
-
- You have access
- Export citation
Elliptic differential operators and diffusion processes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 219-237
-
- Article
-
- You have access
- Export citation
Isometries and certain dynamical systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 239-246
-
- Article
-
- You have access
- Export citation
A chain rule for differentiation with applications to multivariate hermite polynomials
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 247-250
-
- Article
-
- You have access
- Export citation
Nemitsky operators between Orlicz-Sobolev spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 251-269
-
- Article
-
- You have access
- Export citation
The mathematics of hysteresis
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 271-287
-
- Article
-
- You have access
- Export citation
On the commutativity of torsion free rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 289-293
-
- Article
-
- You have access
- Export citation
Compressible matrix rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 295-298
-
- Article
-
- You have access
- Export citation
On the boundary behaviour of Bloch and normal functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 299-305
-
- Article
-
- You have access
- Export citation
Linear systems of nonoscillatory differential equations with delayed arguments
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-314
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
Wave propagation in density stratified fluids
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 315-316
-
- Article
-
- You have access
- Export citation
Minimum mean squared error estimation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 317-318
-
- Article
-
- You have access
- Export citation
The Regge calculus in numerical relativity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 319-320
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 30 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 30 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

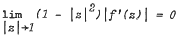 , and criteria for a meromorphic function
, and criteria for a meromorphic function 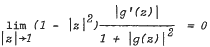 are obtained in terms of the area and the length of the images of hyperbolic disks and hyperbolic circles, respectively.
are obtained in terms of the area and the length of the images of hyperbolic disks and hyperbolic circles, respectively.