Research Article
Common fixed points of two nonexpansive mappings in Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-18
-
- Article
-
- You have access
- Export citation
Dissections of quotients of theta-functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 19-24
-
- Article
-
- You have access
- Export citation
Saturated formations and Sylow normalisers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 25-33
-
- Article
-
- You have access
- Export citation
A fourth-order parabolic equation with a logarithmic nonlinearlity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 35-48
-
- Article
-
- You have access
- Export citation
Quantitative approach to weak noncompactness in the polygon interpolation method
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 49-62
-
- Article
-
- You have access
- Export citation
Pointwise chain recurrent maps of the tree
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 63-68
-
- Article
-
- You have access
- Export citation
On regularity preservation in a semigroup
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 69-86
-
- Article
-
- You have access
- Export citation
Baer-Levi semigroups of partial transformations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 87-106
-
- Article
-
- You have access
- Export citation
On biorthogonal systems and Maxur's intersection property
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 107-111
-
- Article
-
- You have access
- Export citation
A construction of simple Lie subalgebras of certain types from triple systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 113-123
-
- Article
-
- You have access
- Export citation
Approximation by functions with bounded derivative on Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 125-131
-
- Article
-
- You have access
- Export citation
Characteristic polynomials of graph coverings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 133-136
-
- Article
-
- You have access
- Export citation
On rings whose modules of finite length are all cyclic
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-140
-
- Article
-
- You have access
- Export citation
Finite p-groups with normal normalisers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 141-150
-
- Article
-
- You have access
- Export citation
Almost all normal sets are strictly normal
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 151-159
-
- Article
-
- You have access
- Export citation
On tensor factorisation for representations of finite groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-171
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Theta graphs, graph decompositions and related graph labelling techniques
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 173-175
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 69 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 69 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

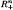 where
where 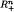 is the set of all vectors
is the set of all vectors