By a result of K.B. Lee, the lattice of varieties of pseudo-complemented distributive lattices is the ω + 1 chain
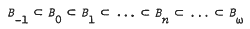
where B−1, B0, B1 are the varieties formed by all trivial, Boolean, and Stone algebras, respectively. General theorems on relative universality proved in the present paper imply that there is a proper class of non-isomorphic algebras in B3 with finite endomorphism monoids, while every infinite algebra from B2 has infinitely many endomorphisms. The variety B4 contains a proper class of non-isomorphic algebras with endomorphism monoids consisting of the identity and finitely many right zeros; on the other hand, any algebra in B3 with a finite endomorphism monoid of this type must be finite.