This paper shows the existence of an infinite family of cyclic balanced ternary designs where the block size is 4, the index 2 and each block contains precisely one repeated element.

Recently in this journal we have shown the similarity between the Kleinecke-Shirokov theorem for subnormal operators and the Fuglede-putnam theorem. The purpose of this paper is to show that this similarity can be generalized to operators which belong to some classes of non-normal operators wider than the class of subnormal operators.

We extend three well-known facts of Fourier series on the disc to Fourier series on the torus, a theorem of Riesz, a theorem of Szegö, and the fact that any function in H1 can be factored as the product of two functions in H2. Here the rôle of negative integers is played by the lattice points in the third quadrant. In earlier extensions of these theorems this rôle was played by half-planes.

Let 〈an〉 be an increasing sequence of real numbers and 〈bn a sequence of positive real numbers. We deal here with the Dirichlet series 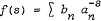and its Laurent expansion at the abscissa of convergence, λ, say. When an and bn behave like

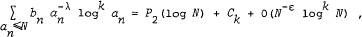
as N → ∞, where P2(x) is a certain polynomial, we obtain the Laurent expansion of f (s) at s = λ, namely

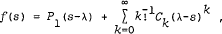
where P1(x) is a polynomial connected with P2(x) above. Also, the connection between P1 and P2 is made intuitively transparent in the proof.

It is proved that a ring satisfying the variable indentity [[xn, y], y] = 0, n = n (x,y) ≥ 1, has nil commutator ideal.

Recently, Visintin gave conditions under which weak convergence in L1 (T;RN) implies strong convergence. Here we analyze such results in terms of associated young measures and present an extension to L1 (T;Ξ), where Ξ is a separable reflexive Banach space.

It is well-known that if W is a set of costant width λ then the circumsphere and the insphere of W are concentric and their radii sum to λ. Here this fact is generalized to sets of constant relative width and it is shown that the result does not depend no W being of constant width, but rather on W satisfying the spherical intersection property; that is, W = ∩{ω + λB:ω ɛ W}.

In this paper we prove a coincidence theorem in not necessarily locally convex topological vector spaces, which contains, as a special case, a coincidence theorem proved by Felix Browder. As an application, a result about the existence of maximal elements is obtained.

We study real hypersurfaces M of a complex projective space and show that a condition on the derivative of the Ricci Tensor of M implies M is locally homogeneous with two or three principal curvatures.

In this paper quasi-codivisible covers are defined and investigated relative to a torsion theory (T, F) on Mod R. It is shown that if (T, F) is cohereditary, then a right R-module M has a quasi-codivisible cover whenever it has a codivisible cover. Moreover, it is shown that if (T, F) is cohereditary, then the universal existence of quasi-codivisible covers implies that the ring R/T (R) must be right perfect. The converse holds when (T, F) is pseudo-hereditary.

An Atsuji space is a metric space X such that each continuous function form X to an arbitrary metric space Y is uniformly continuous. We here present (i) characterizations of metric spaces with Atsuji completions; (ii) Cantor-type theorems for Atsuji spaces; (iii) a fixed point theorem for self-maps of an Atsuji space.

We consider the Cauchy problem x (t) = f (t,x (t)), x (0) = x0 in a nonreflexive Banach space X and for f: T × X → X a weakly continuous vector field. Using a compactness hypothesis involving a weak measure of noncompactness we prove an existence result that generalizes earlier theorems by Chow-Shur, Kato and Cramer-Lakshmikantham-Mitchell.

We consider the Cauchy problem x (t) = f (t,x (t)), x (O) = xO defined in a nonreflexive Banach space and with the vector field f: T × X → X being weakly uniformly continuous. Using a compactness hypothesis that involves the weak measure of noncompactness, we prove that the solution set of the above Cauchy problem is nonempty, connected and compact in .

We sharpen a result of Byers on the existence of periodic points for some continuous expanding maps of the interval and generalize it to some classes of continuous maps of the interval which are not necessarily expanding. We then use these results to construct one-parameter families of continuous maps of the interval which have a bifurcation form fixed points directly to period 3 points together with a series of reverse bifurcations from period 3 points back to fixed points. Consequently, our results also provide examples of one-parameter families of continuous maps of the interval whose topological entropy jumps form zero to some positive number and then changes back to zero as the parameter varies.

Some properties which different definitions or orthogonality in a normed space can possess are considered. It is shown that orthogonality can be defined on any separable space with many of the properties possessed by the usual orthogonality in an inner-product space, but that the possession of a further property forces the space to be isomorphic to a Euclidean space.

We study a notion of smoothness of a norm on a Banach space X which generalizes the notion of uniform differentiability and is formulated in terms of unicity of Hahn Banach extensions of functionals on block subspaces of a fixed Schauder basis S in X. Variants of this notion have already been used in estimating moduli of convexity in some spaces or in fixed point theory. We show that the notion can also be used in studying the convergence of expansions coefficient of elements of X* along the dual basis S*.

Let A be a noncommutative C*-algebra other than M2(I). We show that there exists a completely positive map φ of norm one on A and an element a ɛ A such that φ(a) = a, φ(a*a) = a*a, but φ(aa*) ≠ aa*.