Research Article
The Hahn-Schur Theorem on effect algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-168
-
- Article
-
- You have access
- Export citation
On the Dirichlet problem of elliptic type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-177
-
- Article
-
- You have access
- Export citation
Transformations for complex discrete linear Hamiltonian and symplectic systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 179-191
-
- Article
-
- You have access
- Export citation
Schur property and lP isomorphic copies in Musielak–Orlicz sequence spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 193-210
-
- Article
-
- You have access
- Export citation
Nearly extremal Cohen–Macaulay and Gorenstein algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 211-220
-
- Article
-
- You have access
- Export citation
On the distribution of angles of the Salié sums
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 221-227
-
- Article
-
- You have access
- Export citation
Extension problems and non-Abelian duality for C*-algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 229-238
-
- Article
-
- You have access
- Export citation
An infinite class of identities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 239-246
-
- Article
-
- You have access
- Export citation
Orlicz–Pettis Theorem for λ-multiplier convergent operator series
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 247-252
-
- Article
-
- You have access
- Export citation
Some invariants of Pretzel links
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 253-271
-
- Article
-
- You have access
- Export citation
Composition operators on weighted Bergman-Orlicz spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-287
-
- Article
-
- You have access
- Export citation
A class of iteration methods for the matrix equation A×B = C
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 289-298
-
- Article
-
- You have access
- Export citation
Two Ostrowski type inequalities for the Stieltjes integral of monotonic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 299-311
-
- Article
-
- You have access
- Export citation
Finite groups in which some property of two-generator subgroups is transitive
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 313-320
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 75 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 75 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

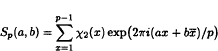
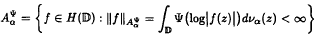
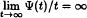 . In fact, under a mild condition on ∞, we show that every holomorphic-self map ∞ of
. In fact, under a mild condition on ∞, we show that every holomorphic-self map ∞ of 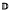 induces a bounded composition operator on
induces a bounded composition operator on 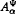 and
and 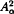 .
.