Contents
Research Article
Isotropic varieties in the singular symplectic geometry
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-169
-
- Article
-
- You have access
- Export citation
On conjugacy classes in finite loops
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 171-176
-
- Article
-
- You have access
- Export citation
A class of nonconvex functions and mathematical programming
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-189
-
- Article
-
- You have access
- Export citation
Commutativity results for rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 191-195
-
- Article
-
- You have access
- Export citation
Recurrence in Lipschitz stable flows
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 197-202
-
- Article
-
- You have access
- Export citation
On a theorem of Li-Banghe and Peterson on immersions of manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 203-205
-
- Article
-
- You have access
- Export citation
On minimal faithful permutation representations of finite groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 207-220
-
- Article
-
- You have access
- Export citation
Fubini's theorem for Radon polymeasures
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 221-229
-
- Article
-
- You have access
- Export citation
Almost periodic solutions of nonlinear parabolic equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 231-238
-
- Article
-
- You have access
- Export citation
On Mosco convergence of convex sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 239-253
-
- Article
-
- You have access
- Export citation
Oscillatory properties of the solutions of linear equations of neutral type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 255-261
-
- Article
-
- You have access
- Export citation
A topological zero-one law for open continuous maps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 263-266
-
- Article
-
- You have access
- Export citation
On commutativity of associative rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 267-271
-
- Article
-
- You have access
- Export citation
On the lattice of right ideals of the endomorphism ring of an abelian group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-291
-
- Article
-
- You have access
- Export citation
New characterisations of pseudocompact spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 293-298
-
- Article
-
- You have access
- Export citation
Automorphisms of certain p-groups (p odd).
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 299-305
-
- Article
-
- You have access
- Export citation
Control point insertion for B-spline curves
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-313
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
Numerical solution of quadratically non-linear boundary value problems using integral equation techniques, with application to nozzle and wall flows
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 315
-
- Article
-
- You have access
- Export citation
A stochastic analysis of scoring systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 317-319
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 38 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
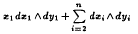 on
on 
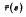 are non- decreasing and
are non- decreasing and  .
.