Let ${{b}_{1}},...,{{b}_{5}}$ be non-zero integers and $n$ any integer. Suppose that ${{b}_{1}}+\cdot \cdot \cdot +{{b}_{5}}\equiv n$ (mod 24) and $\left( {{b}_{i}},{{b}_{j}} \right)=1$ for $1\le i<j\le 5$. In this paper we prove that

1. (i) if all ${{b}_{j}}$ are positive and $n\gg \max {{\left\{ \left| {{b}_{j}} \right| \right\}}^{41+\varepsilon }}$, then the quadratic equation ${{b}_{1}}p_{1}^{2}+\cdot \cdot \cdot +{{b}_{5}}p_{5}^{2}=n$ is soluble in primes ${{p}_{j}}$, and

2. (ii) if ${{b}_{j}}$ are not all of the same sign, then the above quadratic equation has prime solutions satisfying ${{p}_{j}}\ll \sqrt{\left| n \right|}+\max {{\left\{ \left| {{b}_{j}} \right| \right\}}^{20+\varepsilon }}$.

Nous établissons un résultat d’approximation forte pour des processus bivariés ayant une partie gaussienne et une partie empirique. Ce résultat apporte un nouveau point de vue sur deux théorèmes hongrois bidimensionnels établis précédemment, concernant l’approximation par un processus de Kiefer d’un processus empirique uniforme unidimensionnel et l’approximation par un pont brownien bidimensionnel d’un processus empirique uniforme bidimensionnel. Nous les enrichissons un peu et montrons que sous leur nouvelle forme ils ne sont que deux énoncés d’un même résultat.

We study convergence in weighted convolution algebras ${{L}^{1}}\left( \omega \right)$ on ${{R}^{+}}$, with the weights chosen such that the corresponding weighted space $M\left( \omega \right)$ of measures is also a Banach algebra and is the dual space of a natural related space of continuous functions. We determine convergence factor $\eta $ for which weak$*$-convergence of $\left\{ {{\text{ }\!\!\lambda\!\!\text{ }}_{n}} \right\}$ to $\text{ }\!\!\lambda\!\!\text{ }$ in $M\left( \omega \right)$ implies norm convergence of ${{\text{ }\!\!\lambda\!\!\text{ }}_{n}}*f$ to $\text{ }\!\!\lambda\!\!\text{ *}f$ in ${{L}^{1}}\left( \omega \eta \right)$. We find necessary and sufficent conditions which depend on $\omega$ and $f$ and also find necessary and sufficent conditions for $\eta$ to be a convergence factor for all ${{L}^{1}}\left( \omega \right)$ and all $f$ in ${{L}^{1}}\left( \omega \right)$. We also give some applications to the structure of weighted convolution algebras. As a preliminary result we observe that $\eta$ is a convergence factor for $\omega$ and $f$ if and only if convolution by $f$ is a compact operator from $M\left( \omega \right)$ (or ${{L}^{1}}\left( \omega \right)$) to ${{L}^{1}}\left( \omega \eta \right)$.

In this article we state and prove precise theorems on the homotopy classification of graded categorical groups and their homomorphisms. The results use equivariant group cohomology, and they are applied to show a treatment of the general equivariant group extension problem.

We characterize embeddability of algebraic varieties into smooth toric varieties and prevarieties. Our embedding results hold also in an equivariant context and thus generalize a well-known embedding theorem of Sumihiro on quasiprojective $G$-varieties. The main idea is to reduce the embedding problem to the affine case. This is done by constructing equivariant affine conoids, a tool which extends the concept of an equivariant affine cone over a projective $G$-variety to a more general framework.

Let $B$ be the unit ball of ${{\mathbb{C}}^{n}}$ with respect to an arbitrary norm. We prove that the analog of the Carathéodory set, i.e. the set of normalized holomorphic mappings from $B$ into ${{\mathbb{C}}^{n}}$ of “positive real part”, is compact. This leads to improvements in the existence theorems for the Loewner differential equation in several complex variables. We investigate a subset of the normalized biholomorphic mappings of $B$ which arises in the study of the Loewner equation, namely the set ${{S}^{0}}\left( B \right)$ of mappings which have parametric representation. For the case of the unit polydisc these mappings were studied by Poreda, and on the Euclidean unit ball they were studied by Kohr. As in Kohr’s work, we consider subsets of ${{S}^{0}}\left( B \right)$ obtained by placing restrictions on the mapping from the Carathéodory set which occurs in the Loewner equation. We obtain growth and covering theorems for these subsets of ${{S}^{0}}\left( B \right)$ as well as coefficient estimates, and consider various examples. Also we shall see that in higher dimensions there exist mappings in $S(B)$ which can be imbedded in Loewner chains, but which do not have parametric representation.

We introduce the notion of strongly projective graph, and characterise these graphs in terms of their neighbourhood poset. We describe certain exponential graphs associated to complete graphs and odd cycles. We extend and generalise a result of Greenwell and Lovász [6]: if a connected graph $G$ does not admit a homomorphism to $K$, where $K$ is an odd cycle or a complete graph on at least 3 vertices, then the graph $G\,\times \,{{K}^{S}}$ admits, up to automorphisms of $K$, exactly $s$ homomorphisms to $K$.

We study the resonances of the operator $P(h)\,=\,-{{\Delta }_{x}}\,+\,V(x)\,+\,\varphi (hx)$. Here $V$ is a periodic potential, $\varphi $ a decreasing perturbation and $h$ a small positive constant. We prove the existence of shape resonances near the edges of the spectral bands of ${{P}_{0\,}}=\,-{{\Delta }_{x}}\,+\,V(x)$, and we give its asymptotic expansions in powers of ${{h}^{\frac{1}{2}}}$.

We prepare for a comparison of global trace formulas of general linear groups and their metaplectic coverings. In particular, we generalize the local metaplectic correspondence of Flicker and Kazhdan and describe the terms expected to appear in the invariant trace formulas of the above covering groups. The conjectural trace formulas are then placed into a form suitable for comparison.

Generically, one can attach to a $\mathbf{Q}$-curve $C$ octahedral representations $\rho $: $\text{Gal}\left( \mathbf{\bar{Q}}/\mathbf{Q} \right)\,\to \,\text{G}{{\text{L}}_{2}}\left( {{{\mathbf{\bar{F}}}}_{3}} \right)$ coming from the Galois action on the 3-torsion of those abelian varieties of $\text{G}{{\text{L}}_{2}}$-type whose building block is $C$. When $C$ is defined over a quadratic field and has an isogeny of degree 2 to its Galois conjugate, there exist such representations $\rho $ having image into $\text{G}{{\text{L}}_{2}}\left( {{\mathbf{F}}_{9}} \right)$. Going the other way, we can ask which mod 3 octahedral representations $\rho $ of $\text{Gal}\left( \mathbf{\bar{Q}}/\mathbf{Q} \right)$ arise from $\mathbf{Q}$-curves in the above sense. We characterize those arising from quadratic $\mathbf{Q}$-curves of degree 2. The approach makes use of Galois embedding techniques in $\text{G}{{\text{L}}_{2}}\left( {{\mathbf{F}}_{9}} \right)$, and the characterization can be given in terms of a quartic polynomial defining the ${{S}_{4}}$-extension of $\mathbf{Q}$ corresponding to the projective representation $\bar{\rho }$.

We study the cohomology of connected components of Shimura varieties ${{S}_{Kp}}$ coming from the group $\text{GS}{{\text{p}}_{2g}}$, by an approach modeled on the stabilization of the twisted trace formula, due to Kottwitz and Shelstad. More precisely, for each character $\bar{\omega }$ on the group of connected components of ${{S}_{Kp}}$ we define an operator $L(\omega )$ on the cohomology groups with compact supports $H_{c}^{i}\left( {{S}_{Kp,}}{{\overset{-}{\mathop{\mathbb{Q}}}\,}_{\ell }} \right)$, and then we prove that the virtual trace of the composition of $L(\omega )$ with a Hecke operator $f$ away from $p$ and a sufficiently high power of a geometric Frobenius $\Phi _{p}^{r}$, can be expressed as a sum of $\omega$-weighted (twisted) orbital integrals (where $\omega$-weighted means that the orbital integrals and twisted orbital integrals occuring here each have a weighting factor coming from the character $\bar{\omega }$). As the crucial step, we define and study a new invariant ${{\alpha }_{1}}\left( {{\gamma }_{0}};\gamma ,\delta \right)$ which is a refinement of the invariant $\alpha \left( {{\gamma }_{0}},\,\gamma ,\,\delta \right)$ defined by Kottwitz. This is done by using a theorem of Reimann and Zink.

It is shown that simple stably projectionless ${{\text{C}}^{*}}$-algebras which are inductive limits of certain specified building blocks with trivial $\text{K}$-theory are classified by their cone of positive traces with distinguished subset. This is the first example of an isomorphism theorem verifying the conjecture of Elliott for a subclass of the stably projectionless algebras.

We study the moderate growth generalized Whittaker functions, associated to a unitary character $\psi $ of a unipotent subgroup, for the non-tempered cohomological representation of $G\,=\,\text{Sp}\left( 2,\,\mathbb{R} \right)$. Through an explicit calculation of a holonomic system which characterizes these functions we observe that their existence is determined by the including relation between the real nilpotent coadjoint $G$-orbit of $\psi $ in $\mathfrak{g}_{\mathbb{R}}^{*}$ and the asymptotic support of the cohomological representation.

Given a matrix $A$, let $\mathcal{O}\left( A \right)$ denote the orbit of $A$ under a certain group action such as

1. (1) $U\left( m \right)\,\otimes U\left( n \right)$ acting on $m\,\times \,n$ complex matrices $A$ by $(U,\,V)\,*\,A\,=\,UA{{V}^{t}}$,

2. (2) $O\left( m \right)\otimes O\left( n \right)$ or $\text{SO(}m\text{)}\,\otimes \,\text{SO(}n\text{)}$ acting on $m\,\times \,n$ real matrices $A$ by $(U,\,V)\,*\,A\,=\,UA{{V}^{t}}$,

3. (3) $U(n)$ acting on $n\,\times \,n$ complex symmetric or skew-symmetric matrices $A$ by $U\,*\,A\,=\,UA{{U}^{t}}$,

4. (4) $O(n)$ or $\text{SO(n)}$ acting on $n\,\times \,n$ real symmetric or skew-symmetric matrices $A$ by $U\,*\,A\,=\,UA{{U}^{t}}$.

Denote by

1

$$\mathcal{O}({{A}_{1}},\ldots ,{{A}_{k}})\,=\,\{{{X}_{1\,}}+\cdot \cdot \cdot +\,{{X}_{k}}\,:\,{{X}_{i}}\,\in \,\mathcal{O}({{A}_{i}}),i\,=\,1,\ldots ,k\}$$

the joint orbit of the matrices ${{A}_{1}},\ldots ,{{A}_{k}}$. We study the set of diagonals or partial diagonals of matrices in $\mathcal{O}({{A}_{1}},\ldots ,{{A}_{k}})$, i.e., the set of vectors $({{d}_{1}},\ldots {{d}_{r}})$ whose entries lie in the $(1,\,{{j}_{1}}),\ldots ,(r,\,{{j}_{r}})$ positions of a matrix in $\mathcal{O}({{A}_{1}},\ldots ,{{A}_{k}})$ for some distinct column indices ${{j}_{1}},\ldots ,{{j}_{r}}$. In many cases, complete description of these sets is given in terms of the inequalities involving the singular values of ${{A}_{1}},\ldots ,{{A}_{k}}$. We also characterize those extreme matrices for which the equality cases hold. Furthermore, some convexity properties of the joint orbits are considered. These extend many classical results on matrix inequalities, and answer some questions by Miranda. Related results on the joint orbit $\mathcal{O}({{A}_{1}},\ldots ,{{A}_{k}})$ of complex Hermitian matrices under the action of unitary similarities are also discussed.

Let $\mathbf{R}/R$ be a quadratic extension of finite, commutative, local and principal rings of odd characteristic. Denote by ${{\mathbf{U}}_{n}}\left( \mathbf{R} \right)$ the unitary group of rank $n$ associated to $\mathbf{R}/R$. The Weil representation of ${{\mathbf{U}}_{n}}\left( \mathbf{R} \right)$ is defined and its character is explicitly computed.

We investigate the bifurcation of limit cycles in one-parameter unfoldings of quadractic differential systems in the plane having a degenerate critical point at infinity. It is shown that there are three types of quadratic systems possessing an elliptic critical point which bifurcates from infinity together with eventual limit cycles around it. We establish that these limit cycles can be studied by performing a degenerate transformation which brings the system to a small perturbation of certain well-known reversible systems having a center. The corresponding displacement function is then expanded in a Puiseux series with respect to the small parameter and its coefficients are expressed in terms of Abelian integrals. Finally, we investigate in more detail four of the cases, among them the elliptic case (Bogdanov-Takens system) and the isochronous center ${{\mathcal{S}}_{3}}$. We show that in each of these cases the corresponding vector space of bifurcation functions has the Chebishev property: the number of the zeros of each function is less than the dimension of the vector space. To prove this we construct the bifurcation diagram of zeros of certain Abelian integrals in a complex domain.

In this paper, we present a smooth framework for some aspects of the “geometry of CW complexes”, in the sense of Buoncristiano, Rourke and Sanderson. We then apply these ideas to Morse theory, in order to generalize results of Franks and Iriye-Kono.

More precisely, consider a Morse function $f$ on a closed manifold $M$. We investigate the relations between the attaching maps in a $\text{CW}$ complex determined by $f$, and the moduli spaces of gradient flow lines of $f$, with respect to some Riemannian metric on $M$.

We extend the basic theory of Lie algebras of affine algebraic groups to the case of pro-affine algebraic groups over an algebraically closed field $K$ of characteristic 0. However, some modifications are needed in some extensions. So we introduce the pro-discrete topology on the Lie algebra $\mathcal{L}(G)$ of the pro-affine algebraic group $G$ over $K$, which is discrete in the finite-dimensional case and linearly compact in general. As an example, if $L$ is any sub Lie algebra of $\mathcal{L}(G)$, we show that the closure of $\left[ L,\,L \right]$ in $\mathcal{L}(G)$ is algebraic in $\mathcal{L}(G)$.

We also discuss the Hopf algebra of representative functions $H(L)$ of a residually finite dimensional Lie algebra $L$. As an example, we show that if $L$ is a sub Lie algebra of $\mathcal{L}(G)$ and $G$ is connected, then the canonical Hopf algebra morphism from $K\left[ G \right]$ into $H(L)$ is injective if and only if $L$ is algebraically dense in $\mathcal{L}(G)$.

We classify all connected $n$-dimensional complex manifolds admitting effective actions of the unitary group ${{U}_{n}}$ by biholomorphic transformations. One consequence of this classification is a characterization of ${{\mathbb{C}}^{n}}$ by its automorphism group.

We consider the Cauchy problem for the cubic nonlinear Schrödinger equation in one space dimension

1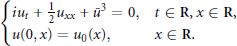

$$\left\{ \begin{align} & i{{u}_{t}}\,+\,\frac{1}{2}{{u}_{xx}}\,+\,{{{\bar{u}}}^{3}}\,=\,0,\,\,\,\,\,t\,\in \,\mathbf{R},\,x\,\in \,\mathbf{R}, \\ & u(0,\,x)\,=\,{{u}_{0}}(x),\,\,\,\,\,\,\,\,\,\,\,x\,\in \,\mathbf{R}. \\ \end{align} \right.$$

Cubic type nonlinearities in one space dimension heuristically appear to be critical for large time. We study the global existence and large time asymptotic behavior of solutions to the Cauchy problem (1). We prove that if the initial data 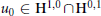${{u}_{0}}\,\in \,{{\mathbf{H}}^{1,\,0}}\,\cap \,{{\mathbf{H}}^{0,\,1}}$ are small and such that 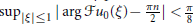${{\sup }_{|\xi |\le 1}}\left| \arg \mathcal{F}{{u}_{0}}(\text{ }\xi \text{ )}\text{0}\frac{\pi n}{2} \right|<\frac{\pi }{8}$ for some n ∈ Z, and 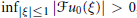${{\inf }_{\left| \xi \right|\le 1}}\,\left| \mathcal{F}{{u}_{0}}(\xi ) \right|\,>\,0$, then the solution has an additional logarithmic timedecay in the short range region 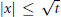$\left| x \right|\,\le \,\sqrt{t}$. In the far region 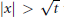$\left| x \right|\,>\,\sqrt{t}$ the asymptotics have a quasilinear character.