We introduce 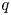$q$-stability conditions 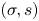$(\sigma,s)$ on Calabi–Yau-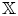$\mathbb {X}$ categories 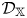$\mathcal {D}_\mathbb {X}$, where 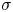$\sigma$ is a stability condition on 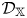$\mathcal {D}_\mathbb {X}$ and 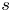$s$ a complex number. 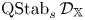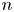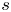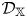We prove the corresponding deformation theorem, that $\operatorname {QStab}_s\mathcal {D}_\mathbb {X}$ is a complex manifold of dimension $n$ for fixed $s$, where $n$ is the rank of the Grothendieck group of $\mathcal {D}_\mathbb {X}$ over 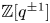$\mathbb {Z}[q^{\pm 1}]$. When $s=N$ is an integer, we show that 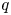$q$-stability conditions can be identified with the stability conditions on 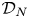$\mathcal {D}_N$, provided the orbit category 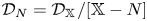$\mathcal {D}_N=\mathcal {D}_\mathbb {X}/[\mathbb {X}-N]$ is well defined. To attack the questions on existence and deformation along the 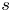$s$ direction, we introduce the inducing method. Sufficient and necessary conditions are given, for a stability condition on an 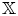$\mathbb {X}$-baric heart (that is, a usual triangulated category) of 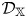$\mathcal {D}_\mathbb {X}$ to induce 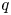$q$-stability conditions on $\mathcal {D}_\mathbb {X}$. As a consequence, we show that the space 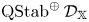$\operatorname {QStab}^\oplus \mathcal {D}_\mathbb {X}$ of (induced) open 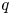$q$-stability conditions is a complex manifold of dimension 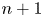$n+1$. Our motivating examples for 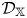$\mathcal {D}_\mathbb {X}$ are coming from (Keller's) Calabi–Yau-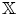$\mathbb {X}$ completions of dg algebras. In the case of smooth projective varieties, the 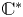$\mathbb {C}^*$-equivariant coherent sheaves on canonical bundles provide the Calabi–Yau-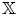$\mathbb {X}$ categories. Another application is that we show perfect derived categories can be realized as cluster-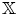$\mathbb {X}$ categories for acyclic quivers.

In this paper we develop a new technique for showing that a nonlinear algebraic differential equation is strongly minimal based on the recently developed notion of the degree of non-minimality of Freitag and Moosa. Our techniques are sufficient to show that generic order $h$ differential equations with non-constant coefficients are strongly minimal, answering a question of Poizat (1980).

We develop the theory of relative regular holonomic $\mathcal {D}$-modules with a smooth complex manifold $S$ of arbitrary dimension as parameter space, together with their main functorial properties. In particular, we establish in this general setting the relative Riemann–Hilbert correspondence proved in a previous work in the one-dimensional case.

We introduce the notion of refined unramified cohomology of algebraic schemes and prove comparison theorems that identify some of these groups with cycle groups. This generalizes to cycles of arbitrary codimension previous results of Bloch–Ogus, Colliot-Thélène–Voisin, Kahn, Voisin, and Ma. We combine our approach with the Bloch–Kato conjecture, proven by Voevodsky, to show that on a smooth complex projective variety, any homologically trivial torsion cycle with trivial Abel–Jacobi invariant has coniveau $1$. This establishes a torsion version of a conjecture of Jannsen originally formulated $\otimes \mathbb {Q}$. We further show that the group of homologically trivial torsion cycles modulo algebraic equivalence has a finite filtration (by coniveau) such that the graded quotients are determined by higher Abel–Jacobi invariants that we construct. This may be seen as a variant for torsion cycles modulo algebraic equivalence of a conjecture of Green. We also prove $\ell$-adic analogues of these results over any field $k$ which contains all $\ell$-power roots of unity.

We develop an effective version of the Chabauty–Kim method which gives explicit upper bounds on the number of $S$-integral points on a hyperbolic curve in terms of dimensions of certain Bloch–Kato Selmer groups. Using this, we give a new ‘motivic’ proof that the number of solutions to the $S$-unit equation is bounded uniformly in terms of $\#S$.