Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 64
TESTING FOR A UNIT ROOT IN THE PRESENCE OF A POSSIBLE BREAK IN TREND
-
- Published online by Cambridge University Press:
- 01 December 2009, pp. 1545-1588
-
- Article
- Export citation
- Cited by 64
ON RATE OPTIMALITY FOR ILL-POSED INVERSE PROBLEMS IN ECONOMETRICS
-
- Published online by Cambridge University Press:
- 11 October 2010, pp. 497-521
-
- Article
- Export citation
- Cited by 63
WHITTLE ESTIMATION OF ARCH MODELS
-
- Published online by Cambridge University Press:
- 27 July 2001, pp. 608-631
-
- Article
- Export citation
- Cited by 63
IDENTIFYING THE BROWNIAN COVARIATION FROM THE CO-JUMPS GIVEN DISCRETE OBSERVATIONS
-
- Published online by Cambridge University Press:
- 19 January 2012, pp. 249-273
-
- Article
- Export citation
- Cited by 63
REALIZED VOLATILITY WHEN SAMPLING TIMES ARE POSSIBLY ENDOGENOUS
-
- Published online by Cambridge University Press:
- 27 November 2013, pp. 580-605
-
- Article
- Export citation
- Cited by 62
LONG MEMORY TESTING IN THE TIME DOMAIN
-
- Published online by Cambridge University Press:
- 06 September 2007, pp. 176-215
-
- Article
- Export citation
- Cited by 61
Adaptive Rules for SeminonparametricEstimators That Achieve AsymptoticNormality
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 307-340
-
- Article
- Export citation
- Cited by 61
COINTEGRATION RANK TESTING UNDERCONDITIONAL HETEROSKEDASTICITY
-
- Published online by Cambridge University Press:
- 22 March 2010, pp. 1719-1760
-
- Article
- Export citation
- Cited by 61
Testing a Parametric Model Against a Semiparametric Alternative
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 821-848
-
- Article
- Export citation
- Cited by 60
STRUCTURAL CHANGE IN AR(1) MODELS
-
- Published online by Cambridge University Press:
- 07 February 2001, pp. 87-155
-
- Article
- Export citation
- Cited by 60
Implications of Aggregation with Common Factors
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 208-222
-
- Article
- Export citation
- Cited by 60
HETEROSKEDASTIC TIME SERIES WITH A UNIT ROOT
-
- Published online by Cambridge University Press:
- 01 October 2009, pp. 1228-1276
-
- Article
- Export citation
- Cited by 60
NONPARAMETRIC SIGNIFICANCE TESTING
-
- Published online by Cambridge University Press:
- 01 August 2000, pp. 576-601
-
- Article
- Export citation
- Cited by 60
THE FUNCTIONAL CENTRAL LIMIT THEOREM AND WEAK CONVERGENCE TO STOCHASTIC INTEGRALS I: Weakly Dependent Processes
-
- Published online by Cambridge University Press:
- 05 October 2000, pp. 621-642
-
- Article
- Export citation
- Cited by 60
On the Shape of the Likelihood/Posterior in Cointegration Models
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 514-551
-
- Article
- Export citation
- Cited by 59
NONPARAMETRIC REGRESSION IN THE PRESENCE OF MEASUREMENT ERROR
-
- Published online by Cambridge University Press:
- 01 December 2004, pp. 1046-1093
-
- Article
- Export citation
- Cited by 59
EFFICIENT ESTIMATION OF FACTOR MODELS
-
- Published online by Cambridge University Press:
- 02 August 2011, pp. 274-308
-
- Article
- Export citation
- Cited by 59
Spurious Break
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 736-749
-
- Article
- Export citation
- Cited by 58
SEMIPARAMETRIC ESTIMATION OF PARTIALLY LINEAR MODELS FOR DEPENDENT DATA WITH GENERATED REGRESSORS
-
- Published online by Cambridge University Press:
- 15 May 2002, pp. 625-645
-
- Article
- Export citation
- Cited by 58
A Graphical Exposition of the Ordered Probit
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 127-131
-
- Article
- Export citation
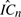 is used, which substantially excludes from RC all terms containing jumps. Unlike in Jacod (
is used, which substantially excludes from RC all terms containing jumps. Unlike in Jacod ( and for further measures of dependence between the two Brownian parts are obtained; the estimation error asymptotic variance is shown to be smaller than for the alternative estimators of IC in the literature; 2) by also selecting the observations as in Hayashi and Yoshida (
and for further measures of dependence between the two Brownian parts are obtained; the estimation error asymptotic variance is shown to be smaller than for the alternative estimators of IC in the literature; 2) by also selecting the observations as in Hayashi and Yoshida (