Contents
Articles
The Cowles Commission, the Brookings Project, and the Econometric Services Industry: Successes and Possible New Directions: A Personal View
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 383-401
-
- Article
- Export citation
The Bias of Bootstrapped Versus Conventional Standard Errors in the General Linear and SUR Models
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 258-275
-
- Article
- Export citation
Miscellanea
On the Best Unbiased Estimate for the Mean of a Short Autoregressive Time Series
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 120-126
-
- Article
- Export citation
Articles
On Efficiency of Methods of Simulated Moments and Maximum Simulated Likelihood Estimation of Discrete Response Models
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 518-552
-
- Article
- Export citation
A Bootstrap Test for Positive Definiteness of Income Effect Matrices
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 276-292
-
- Article
- Export citation
Miscellaneous
Semiparametric IV Estimation with Parameter Dependent Instruments
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 403-406
-
- Article
- Export citation
Miscellanea
A Graphical Exposition of the Ordered Probit
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 127-131
-
- Article
- Export citation
Articles
The Asymptotic Local Structure of the Cox Modified Likelihood-Ratio Statistic for Testing Non-Nested Hypotheses
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 553-569
-
- Article
- Export citation
Photograph Section
The Advisory Board
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 291-292
-
- Article
- Export citation
Book Reviews
A Course in EconometricsArthur Goldberger Harvard University Press, 1991
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 407-412
-
- Article
- Export citation
Book Review
Continuous Time Econometric ModellingA.R. Bergstrom Oxford University Press, 1991
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 571-579
-
- Article
- Export citation
Photograph Section
Two Photographs of Tjalling C. Koopmans
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 133
-
- Article
- Export citation
Book Review
The Statistical Theory of Linear SystemsE. J. Hannan and Manfred Deistler John Wiley & Sons, 1988
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 135-143
-
- Article
- Export citation
Problems
Instrumental Variable Estimation of a Simple Simultaneous Equations Model with a Singular Error Variance Matrix
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 581
-
- Article
- Export citation
Book Reviews
Applied Nonparametric RegressionW. Härdle Cambridge University Press, 1990
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 413-419
-
- Article
- Export citation
Forecasting, Structural Time Series Models and the Kalman Filter, Andrew C. Harvey Cambridge University Press, 1939 - Fore Casting, Structural Time Series Models and The Kalman FilterAdrew C. Harvey Cambridge University Press, 1989
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 293-299
-
- Article
- Export citation
Problems
Can More Information Make You Worse Off??
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 145
-
- Article
- Export citation
Erratum
Bruce E. Hansen, Strong Laws for Dependent Heterogeneous Processes. Econometric Theory 7(1992): 213–221
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 421-422
-
- Article
-
- You have access
- Export citation
Problems
A Derivation of the Limited Information Maximum Likelihood Estimator
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 301-302
-
- Article
- Export citation
A Matrix Equality Applicable in the Analysis of Mean-and-Covariance Structures
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 581-582
-
- Article
- Export citation
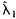 , of the matrix estimate is obtained. This theory applies generally to symmetric, asymptotically normal random matrices. A bootstrap approximation to the distribution of
, of the matrix estimate is obtained. This theory applies generally to symmetric, asymptotically normal random matrices. A bootstrap approximation to the distribution of