Although the national statistics of the notifications of infectious diseases are defective with regard to age and sex, it has been established from the returns of London and other large towns that the mean age of attack from diphtheria has been increasing during the present century. The age shift has been from the pre-school to the school age. Several investigators have commented on the change in age incidence, Murphy (1907) reviewed the trend of mortality in London, and Chalmers (1913) the mortality of Scotland. Cheeseman, Martin & Russell (1939), as a result of an analysis of data kindly provided by the Medical Department of the London County Council, concluded that the change might be due to the decrease in size of family, especially in the more crowded districts. This would Jead to a decrease of morbidity at early ages and, as a consequence, a lower level of herd immunity at school ages, so that the epidemiological experience of the poorer districts would approximate to those of the middle-class districts. In this paper (pp. 188–9) reference was made to Turner's observation (1923) that both in London and Manchester the mean age of attack in epidemic years of scarlet fever was above the average, and it was shown that if the maximum weekly case rate of diphtheria in London (1897–1930) were correlated with the ratio of the number of cases at ages 0–4 to the number at 5–9, a significant negative value was reached. This finding was consistent with Turner's result, but it seemed of interest to apply a slightly more direct test by comparing years of heavy prevalence with adjacent years in which diphtheria was at a lower level.

The Rideal-Walker and Chick-Martin tests depend on end-point methods for comparing bactericides. End-point methods have a number of disadvantages: (1) It is difficult, if not impossible, to estimate end-points accurately. (2) The nature of the test demands a standard time. The results at any standard time will be arbitrary. If the sensitivity of the organisms varies in the two solutions tested, the coefficients obtained will vary with the time chosen as standard. It is impossible to estimate the manner in which the survivor times of the organism are distributed, by end-point methods, and therefore the standard tests in current use do not ascertain whether the result is arbitrary or not. This can only be appreciated if the tests are repeated using different times.

Apart from the difficulties associated with end-points, the coefficients obtained in the present tests are calculated from one concentration of phenol and one concentration of test bactericide. This is also an arbitrary value, for the relative activity of two bactericides will depend on relative values of the concentration exponent, n, for each bactericide; if both phenol and the test bactericide have identical values of n the coefficients will be the same at all concentrations which are compared, but if values of n are different then different coefficients will be obtained for every different concentration compared. As a corollary, unless the value of n for the test bactericide is the same as that of phenol, it is illogical to transfer the phenol coefficient obtained at one concentration to the pure substance, for this procedure implies that the phenol coefficient applies to any concentration of the test bactericide. This is only true when the concentration coefficients of phenol and test bactericide are the same. The standard methods offer no value for n.

All these difficulties can be avoided if the rate of death is followed in both phenol and test bactericide, by viable counts. Two methods of interpreting the results are discussed:

(1) The comparison of reaction rates, calculated by the formula 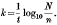This method is complicated by the occurrence of lag period at the start of the reaction between organism and bactericide. This lag period varies in extent in different experiments (often extending up to 50% of the deaths) and makes the interpretation of the results difficult. The lag period has been shown to be a manifestation of, the distribution of logarithmic survival times (Withell, 1942), and is a function of the standard deviation of the logarithmic survivor times (λ). This fact is taken into account in method (2).

(2) The use of the time required for 50% response as a method of comparing bactericides. This time has been symbolized L.t. 50 and is analogous to the lethal dose for the 50% response (l.d. 50) widely used in biological assay. If a logarithmic time scale is used, the logarithmic survival times are found to be approximately normally distributed and consequently probit-logarithm of time lines are straight and in the case of phenol 0·5 % and para-chlor-meta-cresol 0·05% these lines are parallel. In this case a logarithmic time scale means that the comparative times for all percentage responses are equal. In cases where the probit-logarithm-of-time lines are not parallel this would indicate that the standard is unsuitable for the test, for any methods of assay based on a use of a standard to which the organism gives a different response-time relation from that which they give to the test substance or bactericide, are likely to give arbitrary results.

L.T. 50 has been chosen because of the simplicity of the idea underlying it, and because a similar function, L.D. 50, has been used with success in biological assay work. There is also a solid mathematical backing for the use of L.D. 50 in assays involving biological response.

It is suggested that by means of l.t. 50, phenol and the test bactericide can be compared in the following way:

(a) determine the relative speeds of action of the two solutions at any convenient concentrations;

(b) determine the concentration coefficient (ή) of both phenol and test bactericide by means of comparative l.t. 50 values;

(c) determine the temperature coefficient for each substance by similar methods.

From these observations the relative efficiency of the two bactericides can be calculated at any temperature and concentration. If two sets of figures are obtained, one with a vegetative organism, and the other with a sporing organism, a great deal of information can be summarized. It has been shown that an 0·05% solution of parachlor-meta-cresol is approximately one and a half times as efficient as an 0·5% phenol solution (against a Micrococcus). The comparative figure is about 1·0 when Bact. coli is used.

A new form of photo-electric photometer or colorimeter is described which permits of accurate and objective readings in a wide range of colorimetric work with small quantities of solutions. The instrument is of the null-point type and hence requires calibration to suit the particular estimation.

The writer is indebted to the Earl of Moray Fund of the University of Edinburgh for financial assistance towards the expenses of the earlier part of the work.

The original model was made by A. H. Baird of Edinburgh, the model described above by Wm. Watson and Sons, London, to whom, and to Mr W. E. Watson-Baker, I am indebted for suggestions on a number of points.

1. The vitamin C in the dietary of an institution was largely destroyed by the methods of cooking and distribution.

2. Some 50 mg. of ascorbic acid per head per day were required to be added to the diet to produce an optimum excretion level.

3. Large doses of ascorbic acid were given to a group of adolescents in the institution over a period of several months. A record was kept of the incidences of infectious diseases in this treated group and in the remainder (controls). The following conclusions were reached:

(a) The incidences of common cold and tonsillitis were the same in the two groups.

(b) The average duration of illness due to the common cold was the same in the two groups.

(c) The duration of illness of tonsillitis was longer in the control group than in the test group.

(d) Cases of rheumatic fever and pneumonia occurred in the control group but no case of either disease occurred in the test group.

Before the war diphtheria, measles, tuberculosis and whooping cough were the most important of the better-defined causes of death amongst young children in the London area. The large numbers of deaths registered from these four diseases in the age group 0–4 years in the Metropolitan Boroughs alone between 1931 and 1938, together with the deaths recorded under bronchitis and pneumonia, are set out in Table 1.

The principle of the aerosol centrifuge is described, and an elementary mathematicaltreatment is given.

The relations between the behaviour of the centrifuge and its dimensions, speed and airflow have been tested experimentally on three machines. It is shown that the mathe-matical formulae given are an adequate basis for design.

Various applications are mentioned.

A study of the growth phases of pleuropneumoma has been carried out by two new methods: (1) a new fixing and staining technique, (2) a new dark-ground method. The results obtained by the two methods are in good agreement, and the life cycle of the organism of bovine pleuropneumoma and related microbes as revealed by means of both methods has been described.

1. The incidence of cross-infection with Str. pyogenes during a period of four months was compared in two blocks occupied by scarlet-fever patients. One block was nursed by the bed isolation method and the other by the ordinary method in current use for multiple-bed wards. 2. The rules for the bed isolation blook are given. 3. The incidence of cross-infection with Str. pyogenes among patients in the bed isolation block was 20·3%, that among patients in the ordinary block 22·6%. 4. We concluded that the bed isolation nursing technique practised was not effective in reducing cross-infection with Str. pyogenes among scarlet-fever patients. 5. A further test of bed isolation nursing was made for six months, using the extra precaution of vacuum-cleaning the floors. We found that crossinfection was still occurring, but the incidence could not be estimated since the Str. pyogenes strains isolated had to be destroyed at the outbreak of war. At this time the serological typing had not been completed. 6. The importance of dust-borne and droplet-borne infection in addition to that of contact infection is discussed. The type of investigation required to decide whether cross-infection in multiple-bed scarlet-fever wards can be eliminated by the methods at our present disposal is outlined.

1. In a controlled experiment prontosil was used in the treatment of four cases of streptococcal tonsillitis. These cases subsequently developed acute rheumatism.

2. Two cases of otitis media and one case of streptococcal pneumonia, not in the controlled experiment, were treated with sulphonamide and sulphapyridine respectively. These cases developed rheumatism as a complication.

3. Haemolytic streptococci were recovered from twelve cases of respiratory tract infection which subsequently developed acute rheumatic fever.

Investigations at two hospitals, P and S, showed Staphylococcus aureus to be commonly present in the milk of healthy nursing mothers and the throat and intestine of their babies. In hospital P, the proportion affected in a group of eighty-two mothers and their babies was over 90%. The condition may not be uncommon in maternity hospitals, but no information of its occurrence is available from private obstetrical practice. The cocci concerned seemed to be of low virulence, for babies swallowing relatively massive doses in their mothers' milk suffered no perceptible ill effect. On the other hand, the coccus was found in the pus of the only case of breast abscess encountered, and in some minor external pustular lesions. It was present in the milk of all the cases of flushed breast examined, but its causal connexion with this condition awaits proof.

The staphylococci, in the majority of cases, seemed to occur first in the baby's throat, possibly from a focus of infection in the babies' ward, and to be transmitted from baby to baby and from baby to mother, with a return infection, in larger amount, through the mother's milk. The mother's nose and throat must be included amongst other, but less frequent, sources of the infection.

The predominating type of Staph. aureus gave a relatively strong coagulase reaction which was caused only by actively growing cocci, but it would seem that the reaction caused by this agency is less trustworthy as an index of virulence of the coccus than one in which free coagulase also operates.

The new data presented show that the life cycle of the L1 organism separated from cultures of Streptobacillus moniliformis corresponds in many respects to that of pleuropneumonia. It seems therefore justifiable to classify it with the group of pleuropneumonia-like organisms and not with the bacteria. Its peculiar life cycle, including the formation of elementary reproductive corpuscles, a process previously described for pleuropneumonia, but not occurring in bacteria, is regarded as strong evidence in favour of the conception that Str. moniliformis is composed of two genetically different microbes, a Streptobacillus and the LI organism. Cross-absorption tests between Str. moniliformis and the LI organism have shown that these organisms possess different serological affinities.

A Proteus-like organism is described, which produced acid but no gas in carbohydrate media.

I wish to thank Dr W. D. Carruthers,. Medical Officer of Health of Staffordshire, for permission to publish this paper.

1. A review has been made of literature on the ecology of different types of coliform bacteria. The main object of the review has been to consider whether there is evidence to support the view that Bact. aerogenes and the intermediate types live normally on plants or in the soil and not in the intestines of man and other animals.

2. There is ample evidence that Bact. coli is by far the most common type of coliform in normal human faeces. On the other hand, there is evidence that Bact. aerogenes or intermediate types are usually present in faeces, may sometimes be present in greater numbers than Bact. coli, and on rare occasions may be the only type present. Both quantitatively and qualitatively the coliform flora of the faeces of an individual person may vary from day to day. There is insufficient evidence on the numbers of Bact. aerogenes and intermediate types in faeces to justify any more definite statement, but limited data suggest that such types may be absent or may be present in numbers of the order of a million per gram.

3. When fresh faeces are stored there is first a multiplication of such bacteria as will grow on ordinary laboratory media, including the coliform types. The rate of multiplication, as with the flora of soil, water, and milk, increases with an increase in the incubation temperature to 37° C, but the period of multiplication becomes shorter. In the literature consulted no evidence can be found to show which groups are prominent in the multiplication. Results are in agreement that on further storage the ratio of the numbers of Bact. coli to those of Bact. aerogenes and intermediates decreases, the typical Bact. coli flora dying off more rapidly than other conform types. The rapidity of decrease appears to depend partially at least upon the temperature of the environment, and the decrease may be accelerated by intense sunlight.

4. In urine from patients suffering from genito-urinary infections the dominant types of coliform are usually either Bact. aerogenes or intermediates. No data on the number of such organisms in urine have been obtained from the works consulted.

5. There is no-evidence that coliform bacteria multiply on fresh grasses or grains. Few quantitative data on this question have been found. In some of the older work it is doubtful whether a large proportion of the cultures isolated were actually coliform bacteria or whether they were species of other genera capable of fermenting lactose at 30° C. but not at 37° C. In the decomposition of grasses and legumes during ensilage, a process involving a considerable increase in temperature, it would appear that multiplication of conform bacteria may take place and counts may for a time equal those found in fresh faeces. No indication has been found that this multiplication is confined to Bact. aerogenes or intermediates.

6. Most workers who have studied the coliform bacteria in soil have ignored the quantitative aspects and no counts at intervals over long periods of coliform bacteria in any undisturbed soil appear to have been made. No evidence of any multiplication of coliform bacteria in soil has been found. Results, however, are in agreement that where pollution of the soil by animal excreta has taken place, the heavier the pollution the greater is the number of coliform bacteria; soils relatively free from human or other animal pollution either contain no coliform bacteria or only small numbers. It is generally agreed that the ratio of the numbers of Bact. coli to those of Bact. aerogenes and intermediates decreases with the increase of time which has elapsed since pollution of the soil. This change is similar to that which occurs in faeces during storage.

7. There is insufficient evidence to justify the definite statement often made that Bact. aerogenes and intermediates are normal inhabitants of soils, grasses, and grains.

1. The circumstances attending an outbreak of haemolytic streptococcal infection in a training centre, followed by acute rheumatism, are described.

2. The incidence of streptococcal infections in trained men and apprentices was 64 and 474 per 1000 respectively.

3. Of streptococcal infections 78·0% occurred in members of two younger classes of apprentices.

4. The eight cases of acute rheumatism were all in apprentices, seven cases being in the same two classes. All but one case had had tonsillitis or scarlatina during the epidemic.

5. The smallest percentage of post-epidemic Dick-positive reactors was found in the youngest class which had suffered most in the outbreak.

The mean time-survivor curves of bacteria immersed in two phenolic disinfectants show the same variation of type as the individual curves, that is, (a) an exponential rate, (b) a lag phase followed by an exponential rate. The significance of all these curves and of others is discussed in the next part of the paper.

The question formulated in the introduction to this report can now be answered. Ozone in tolerable concentration is able to inactivate certain bacteria when these are present as unprotected singleton aerosol particles in atmospheres of 60–90% R.h. When such bacteria are covered with a protective coating of organic matter, however, as in aerosols naturally emitted during a sneeze or cough, then ozone in permissible concentration is without significant effect. Inactivation of such protected organisms can only be achieved by the use of ozone in decidedly higher concentrations, which must be deemed dangerous for prolonged spells of breathing. Bacteria that have settled on surfaces are generally more resistant to ozone than when in newly formed aerosols. Hence experimental evidence leads to the conclusion that ozone, in concentrations that can be breathed over long periods without irritation, cannot be expected to provide any effective protection against air-borne bacterial infection, through direct inactivation of the infectious carrier particles.

Although multiple cases of acute rheumatism have been observed to follow waves of streptococcal infection in institutions (see Green, p. 369) there is doubt as to whether acuter heumatism itself becomes epidemic under such circumstances or whether the element of infectivity lies in the preliminary throat infection as concluded by Sheldon (1931).

1. The authors concluded in a previous paper that the most reliable single test for the detection of Bact. coli was incubation in MacConkey's broth at 44° C, such a test for Bact. coli alone being necessary in shellfish because of occasional multiplication of other coliforms in purified mussels. The present investigation is an attempt to verify this finding on a broader basis.

2. A description is given of the isolation of 1600 cultures of coliform organisms from polluted mussels, sewage, and faeces (human, cow, sheep and sea birds). Their classification according to ‘IMViC’ reactions and the production of gas in MacConkey's broth at temperatures of 37, 41, 44, 45 and 46° C. is given.

3. Of the + + − − type, 1036 out of 1065 cultures (97·3%) were found to produce gas in MacConkey's broth at 44° C. A balance is noted between the + + − − type which does not produce gas at 44° C. (irregular I) and the two irregular types which do so (irregular II and irregular VI). Such a balance was reported by Bardsley (1938).

4. From the cultures examined it is confirmed that incubation at 44° C. is the most suitable temperature for use with MacConkey's broth for permitting the maximum number of Bact. coli to produce gas while inhibiting the maximum number of other coliforms.

1. Four β-haemolytic strains of Streptococcus, suspended in normal saline, showed progressive increase in mortality, as the pHwas lowered from 7·5 to 5·0; below pH 5·0 the mortality was greatly accentuated.

2. Ether and alcohol extracts of human skin and its appendages were powerfully, saline extracts more weakly and inconstantly, lethal to the haemolytic Streptococcus and to certain other organisms.

3. The long chain fatty acids and soaps are the chief, if not the only, bactericidal constituents of skin and its appendages.

4. Experiments are described illustra ting the streptococcocidal effect of various acids occurring in animal fats.

5. Cystein and blood inhibit the streptoeoccocidal activity of skin fats and certain fatty acids. Ultra-violet light may increase this activity, or abolish, the inhibition exercised by cystein.

6. The mechanism of the sterilizing power of fatty acids and soaps, the influence exerted by cystein, blood, and ultra-violet light on the sterilizing power, of skin fats and fatty acids, and the relationship of skin fatty acids to lysozyme are discussed.

Owing to the entry of Japan into the war it is essential that agar should be used as economically as possible. Since October 1941, we have, in this laboratory, reclaimed used agar by the following simple method, which is a modification of the procedure described by Huang, Shen & Tang (1941).