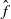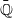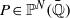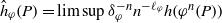Contents
Review Article
Lyapunov spectrum of invariant subbundles of the Hodge bundle
-
- Published online by Cambridge University Press:
- 05 December 2012, pp. 353-408
-
- Article
- Export citation
Research Article
Dynamics of homeomorphisms of the torus homotopic to Dehn twists
-
- Published online by Cambridge University Press:
- 15 January 2013, pp. 409-422
-
- Article
- Export citation
Singular measures for class P-circle homeomorphisms with several break points
-
- Published online by Cambridge University Press:
- 30 November 2012, pp. 423-456
-
- Article
- Export citation
Geometric realization for substitution tilings
-
- Published online by Cambridge University Press:
- 05 December 2012, pp. 457-482
-
- Article
- Export citation
The entropy of a special overlapping dynamical system
-
- Published online by Cambridge University Press:
- 30 November 2012, pp. 483-500
-
- Article
- Export citation
Lyapunov exponents in Hilbert geometry
-
- Published online by Cambridge University Press:
- 03 December 2012, pp. 501-533
-
- Article
- Export citation
Quantitative ergodic theorems for weakly integrable functions
-
- Published online by Cambridge University Press:
- 29 November 2012, pp. 534-542
-
- Article
- Export citation
Centralizers of rank-one homeomorphisms
-
- Published online by Cambridge University Press:
- 03 December 2012, pp. 543-556
-
- Article
- Export citation
Classical motion in random potentials
-
- Published online by Cambridge University Press:
- 05 December 2012, pp. 557-593
-
- Article
- Export citation
The metric entropy of random dynamical systems in a Banach space: Ruelle inequality
-
- Published online by Cambridge University Press:
- 15 November 2012, pp. 594-615
-
- Article
- Export citation
Meromorphic non-integrability of a steady Stokes flow inside a sphere
-
- Published online by Cambridge University Press:
- 15 November 2012, pp. 616-627
-
- Article
- Export citation
Hyperbolization of cocycles by isometries of the Euclidean space
-
- Published online by Cambridge University Press:
- 05 December 2012, pp. 628-646
-
- Article
- Export citation
Dynamical degree, arithmetic entropy, and canonical heights for dominant rational self-maps of projective space
-
- Published online by Cambridge University Press:
- 29 November 2012, pp. 647-678
-
- Article
- Export citation
Medvedev degrees of two-dimensional subshifts of finite type
-
- Published online by Cambridge University Press:
- 29 November 2012, pp. 679-688
-
- Article
- Export citation
Basins of attraction of automorphisms in ℂ3
-
- Published online by Cambridge University Press:
- 15 November 2012, pp. 689-692
-
- Article
- Export citation
Persistent massive attractors of smooth maps
-
- Published online by Cambridge University Press:
- 23 November 2012, pp. 693-704
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 34 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
COM volume 34 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 March 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation