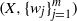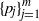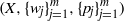Contents
Back Cover (IBC, OBC) and matter
ETS volume 33 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 02 May 2013, pp. b1-b4
-
- Article
-
- You have access
- Export citation
Research Article
An L1 ergodic theorem with values in a non-positively curved space via a canonical barycenter map
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 609-623
-
- Article
- Export citation
Hubbard forests
-
- Published online by Cambridge University Press:
- 08 November 2011, pp. 303-317
-
- Article
- Export citation
Invariant measures with bounded variation densities for piecewise area preserving maps
-
- Published online by Cambridge University Press:
- 14 February 2012, pp. 624-642
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 33 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 07 January 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Ruelle operator with weakly contractive iterated function systems
-
- Published online by Cambridge University Press:
- 31 August 2012, pp. 1265-1290
-
- Article
- Export citation
Back Cover (IBC, OBC) and matter
ETS volume 33 issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 29 August 2013, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Correction
Nonabelian free group actions: Markov processes, the Abramov–Rohlin formula and Yuzvinskii’s formula – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 06 September 2012, pp. 643-645
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 33 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 15 July 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
ETS volume 33 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 07 January 2013, pp. b1-b9
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC and matter
ETS volume 33 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 15 July 2013, pp. f1-f8
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETDS volume 33 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 March 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
ETDS volume 33 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 06 March 2013, pp. b1-b3
-
- Article
-
- You have access
- Export citation