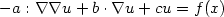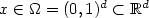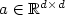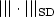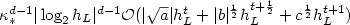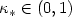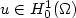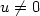Refine listing
Actions for selected content:
Contents
Research Article
Convergence of implicit Finite Volume methods for scalar conservation laws with discontinuous flux function
-
- Published online by Cambridge University Press:
- 04 July 2008, pp. 699-727
-
- Article
- Export citation
A variational model in image processing with focal points
-
- Published online by Cambridge University Press:
- 04 July 2008, pp. 729-748
-
- Article
- Export citation
Finite element approximation of a two-layered liquid filmin the presence of insoluble surfactants
-
- Published online by Cambridge University Press:
- 30 July 2008, pp. 749-775
-
- Article
- Export citation
Sparse finite element approximation of high-dimensional transport-dominated diffusion problems
-
- Published online by Cambridge University Press:
- 30 July 2008, pp. 777-819
-
- Article
- Export citation
The hp-version of the boundary element method with quasi-uniform meshes in three dimensions
-
- Published online by Cambridge University Press:
- 04 July 2008, pp. 821-849
-
- Article
- Export citation
A Roe-type scheme for two-phase shallow granular flows over variable topography
-
- Published online by Cambridge University Press:
- 30 July 2008, pp. 851-885
-
- Article
- Export citation
The change in electric potential due to lightning
-
- Published online by Cambridge University Press:
- 04 July 2008, pp. 887-901
-
- Article
- Export citation