We prove the compatibility of local and global Langlands correspondences for $\operatorname {GL}_n$ up to semisimplification for the Galois representations constructed by Harris-Lan-Taylor-Thorne [10] and Scholze [18]. More precisely, let $r_p(\pi )$ denote an n-dimensional p-adic representation of the Galois group of a CM field F attached to a regular algebraic cuspidal automorphic representation $\pi $ of $\operatorname {GL}_n(\mathbb {A}_F)$. We show that the restriction of $r_p(\pi )$ to the decomposition group of a place $v\nmid p$ of F corresponds up to semisimplification to $\operatorname {rec}(\pi _v)$, the image of $\pi _v$ under the local Langlands correspondence. Furthermore, we can show that the monodromy of the associated Weil-Deligne representation of $\left .r_p(\pi )\right |{}_{\operatorname {Gal}_{F_v}}$ is ‘more nilpotent’ than the monodromy of $\operatorname {rec}(\pi _v)$.

The K-theoretic Schur P- and Q-functions $G\hspace {-0.2mm}P_\lambda $ and $G\hspace {-0.2mm}Q_\lambda $ may be concretely defined as weight-generating functions for semistandard shifted set-valued tableaux. These symmetric functions are the shifted analogues of stable Grothendieck polynomials and were introduced by Ikeda and Naruse for applications in geometry. Nakagawa and Naruse specified families of dual K-theoretic Schur P- and Q-functions $g\hspace {-0.1mm}p_\lambda $ and $g\hspace {-0.1mm}q_\lambda $ via a Cauchy identity involving $G\hspace {-0.2mm}P_\lambda $ and $G\hspace {-0.2mm}Q_\lambda $. They conjectured that the dual power series are weight-generating functions for certain shifted plane partitions. We prove this conjecture. We also derive a related generating function formula for the images of $g\hspace {-0.1mm}p_\lambda $ and $g\hspace {-0.1mm}q_\lambda $ under the $\omega $ involution of the ring of symmetric functions. This confirms a conjecture of Chiu and the second author. Using these results, we verify a conjecture of Ikeda and Naruse that the $G\hspace {-0.2mm}Q$-functions are a basis for a ring.

For certain quasismooth Calabi–Yau hypersurfaces in weighted projective space, the Berglund-Hübsch-Krawitz (BHK) mirror symmetry construction gives a concrete description of the mirror. We prove that the minimal log discrepancy of the quotient of such a hypersurface by its toric automorphism group is closely related to the weights and degree of the BHK mirror. As an application, we exhibit klt Calabi–Yau varieties with the smallest known minimal log discrepancy. We conjecture that these examples are optimal in every dimension.

We show that the independence number of $ G_{n,p}$ is concentrated on two values if $ n^{-2/3+ \epsilon } < p \le 1$. This result is roughly best possible as an argument of Sah and Sawhney shows that the independence number is not, in general, concentrated on two values for $ p = o ( (\log (n)/n)^{2/3} )$. The extent of concentration of the independence number of $ G_{n,p}$ for $ \omega (1/n) < p \le n^{-2/3}$ remains an interesting open question.

We investigate an inverse boundary value problem of determination of a nonlinear law for reaction-diffusion processes, which are modeled by general form semilinear parabolic equations. We do not assume that any solutions to these equations are known a priori, in which case the problem has a well-known gauge symmetry. We determine, under additional assumptions, the semilinear term up to this symmetry in a time-dependent anisotropic case modeled on Riemannian manifolds, and for partial data measurements on ${\mathbb R}^n$.

Moreover, we present cases where it is possible to exploit the nonlinear interaction to break the gauge symmetry. This leads to full determination results of the nonlinear term. As an application, we show that it is possible to give a full resolution to classes of inverse source problems of determining a source term and nonlinear terms simultaneously. This is in strict contrast to inverse source problems for corresponding linear equations, which always have the gauge symmetry. We also consider a Carleman estimate with boundary terms based on intrinsic properties of parabolic equations.

We provide a fine description of the weak limit of sequences of regular axisymmetric maps with equibounded neo-Hookean energy, under the assumption that they have finite surface energy. We prove that these weak limits have a dipole structure, showing that the singular map described by Conti and De Lellis is generic in some sense. On this map, we provide the explicit relaxation of the neo-Hookean energy. We also make a link with Cartesian currents showing that the candidate for the relaxation we obtained presents strong similarities with the relaxed energy in the context of $\mathbb {S}^2$-valued harmonic maps.

Dirac rings are commutative algebras in the symmetric monoidal category of $\mathbb {Z}$-graded abelian groups with the Koszul sign in the symmetry isomorphism. In the prequel to this paper, we developed the commutative algebra of Dirac rings and defined the category of Dirac schemes. Here, we embed this category in the larger $\infty $-category of Dirac stacks, which also contains formal Dirac schemes, and develop the coherent cohomology of Dirac stacks. We apply the general theory to stable homotopy theory and use Quillen’s theorem on complex cobordism and Milnor’s theorem on the dual Steenrod algebra to identify the Dirac stacks corresponding to $\operatorname {MU}$ and $\mathbb {F}_p$ in terms of their functors of points. Finally, in an appendix, we develop a rudimentary theory of accessible presheaves.

We prove a decomposition theorem for the nef cone of smooth fiber products over curves, subject to the necessary condition that their Néron–Severi space decomposes. We apply it to describe the nef cone of so-called Schoen varieties, which are the higher-dimensional analogues of the Calabi–Yau threefolds constructed by Schoen. Schoen varieties give rise to Calabi–Yau pairs, and in each dimension at least three, there exist Schoen varieties with nonpolyhedral nef cone. We prove the Kawamata–Morrison–Totaro cone conjecture for the nef cones of Schoen varieties, which generalizes the work by Grassi and Morrison.

We introduce a new concept of rank – relative rank associated to a filtered collection of polynomials. When the filtration is trivial, our relative rank coincides with Schmidt rank (also called strength). We also introduce the notion of relative bias. The main result of the paper is a relation between these two quantities over finite fields (as a special case, we obtain a new proof of the results in [21]). This relation allows us to get an accurate estimate for the number of points on an affine variety given by a collection of polynomials which is of high relative rank (Lemma 3.2). The key advantage of relative rank is that it allows one to perform an efficient regularization procedure which is polynomial in the initial number of polynomials (the regularization process with Schmidt rank is far worse than tower exponential). The main result allows us to replace Schmidt rank with relative rank in many key applications in combinatorics, algebraic geometry, and algebra. For example, we prove that any collection of polynomials $\mathcal P=(P_i)_{i=1}^c$ of degrees $\le d$ in a polynomial ring over an algebraically closed field of characteristic $>d$ is contained in an ideal $\mathcal I({\mathcal Q})$, generated by a collection ${\mathcal Q}$ of polynomials of degrees $\le d$ which form a regular sequence, and ${\mathcal Q}$ is of size $\le A c^{A}$, where $A=A(d)$ is independent of the number of variables.

We give an elementary symmetric function expansion for the expressions $M\Delta _{m_\gamma e_1}\Pi e_\lambda ^{\ast }$ and $M\Delta _{m_\gamma e_1}\Pi s_\lambda ^{\ast }$ when $t=1$ in terms of what we call $\gamma $-parking functions and lattice $\gamma $-parking functions. Here, $\Delta _F$ and $\Pi $ are certain eigenoperators of the modified Macdonald basis and $M=(1-q)(1-t)$. Our main results, in turn, give an elementary basis expansion at $t=1$ for symmetric functions of the form $M \Delta _{Fe_1} \Theta _{G} J$ whenever F is expanded in terms of monomials, G is expanded in terms of the elementary basis, and J is expanded in terms of the modified elementary basis $\{\Pi e_\lambda ^\ast \}_\lambda $. Even the most special cases of this general Delta and Theta operator expression are significant; we highlight a few of these special cases. We end by giving an e-positivity conjecture for when t is not specialized, proposing that our objects can also give the elementary basis expansion in the unspecialized symmetric function.

In the article [CEGS20b], we introduced various moduli stacks of two-dimensional tamely potentially Barsotti–Tate representations of the absolute Galois group of a p-adic local field, as well as related moduli stacks of Breuil–Kisin modules with descent data. We study the irreducible components of these stacks, establishing, in particular, that the components of the former are naturally indexed by certain Serre weights.

We prove that, for any countable acylindrically hyperbolic group G, there exists a generating set S of G such that the corresponding Cayley graph $\Gamma (G,S)$ is hyperbolic, $|\partial \Gamma (G,S)|>2$, the natural action of G on $\Gamma (G,S)$ is acylindrical and the natural action of G on the Gromov boundary $\partial \Gamma (G,S)$ is hyperfinite. This result broadens the class of groups that admit a non-elementary acylindrical action on a hyperbolic space with a hyperfinite boundary action.

In the present paper, we study a new kind of anabelian phenomenon concerning the smooth pointed stable curves in positive characteristic. It shows that the topology of moduli spaces of curves can be understood from the viewpoint of anabelian geometry. We formulate some new anabelian-geometric conjectures concerning tame fundamental groups of curves over algebraically closed fields of characteristic $p>0$ from the point of view of moduli spaces. The conjectures are generalized versions of the Weak Isom-version of the Grothendieck conjecture for curves over algebraically closed fields of characteristic $p>0$ which was formulated by Tamagawa. Moreover, we prove that the conjectures hold for certain points lying in the moduli space of curves of genus $0$.

Let $\overline {\mathcal {M}}_{g, m|n}$ denote Hassett’s moduli space of weighted pointed stable curves of genus g for the heavy/light weight data

$$\begin{align*}\left(1^{(m)}, 1/n^{(n)}\right),\end{align*}$$

and let $\mathcal {M}_{g, m|n} \subset \overline {\mathcal {M}}_{g, m|n}$ be the locus parameterizing smooth, not necessarily distinctly marked curves. We give a change-of-variables formula which computes the generating function for $(S_m\times S_n)$-equivariant Hodge–Deligne polynomials of these spaces in terms of the generating functions for $S_{n}$-equivariant Hodge–Deligne polynomials of $\overline {\mathcal {M}}_{g,n}$ and $\mathcal {M}_{g,n}$.

We extend the Becker–Kechris topological realization and change-of-topology theorems for Polish group actions in several directions. For Polish group actions, we prove a single result that implies the original Becker–Kechris theorems, as well as Sami’s and Hjorth’s sharpenings adapted levelwise to the Borel hierarchy; automatic continuity of Borel actions via homeomorphisms and the equivalence of ‘potentially open’ versus ‘orbitwise open’ Borel sets. We also characterize ‘potentially open’ n-ary relations, thus yielding a topological realization theorem for invariant Borel first-order structures. We then generalize to groupoid actions and prove a result subsuming Lupini’s Becker–Kechris-type theorems for open Polish groupoids, newly adapted to the Borel hierarchy, as well as topological realizations of actions on fiberwise topological bundles and bundles of first-order structures.

Our proof method is new even in the classical case of Polish groups and is based entirely on formal algebraic properties of category quantifiers; in particular, we make no use of either metrizability or the strong Choquet game. Consequently, our proofs work equally well in the non-Hausdorff context, for open quasi-Polish groupoids and more generally in the point-free context, for open localic groupoids.

We study the distribution of the length of longest increasing subsequences in random permutations of n integers as n grows large and establish an asymptotic expansion in powers of $n^{-1/3}$. Whilst the limit law was already shown by Baik, Deift and Johansson to be the GUE Tracy–Widom distribution F, we find explicit analytic expressions of the first few finite-size correction terms as linear combinations of higher order derivatives of F with rational polynomial coefficients. Our proof replaces Johansson’s de-Poissonization, which is based on monotonicity as a Tauberian condition, by analytic de-Poissonization of Jacquet and Szpankowski, which is based on growth conditions in the complex plane; it is subject to a tameness hypothesis concerning complex zeros of the analytically continued Poissonized length distribution. In a preparatory step an expansion of the hard-to-soft edge transition law of LUE is studied, which is lifted to an expansion of the Poissonized length distribution for large intensities. Finally, expansions of Stirling-type approximations and of the expected value and variance of the length distribution are given.

We show that, for an arbitrary finite-dimensional quasi-reductive Lie superalgebra over ${\mathbb {C}}$ with a triangular decomposition and a character $\zeta $ of the nilpotent radical, the associated Backelin functor $\Gamma _\zeta $ sends Verma modules to standard Whittaker modules provided the latter exist. As a consequence, this gives a complete solution to the problem of determining the composition factors of the standard Whittaker modules in terms of composition factors of Verma modules in the category ${\mathcal {O}}$. In the case of the ortho-symplectic Lie superalgebras, we show that the Backelin functor $\Gamma _\zeta $ and its target category, respectively, categorify a q-symmetrizing map and the corresponding q-symmetrized Fock space associated with a quasi-split quantum symmetric pair of type $AIII$.

In 1964, Erdős proposed the problem of estimating the Turán number of the d-dimensional hypercube 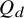$Q_d$. Since 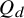$Q_d$ is a bipartite graph with maximum degree d, it follows from results of Füredi and Alon, Krivelevich, Sudakov that 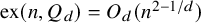$\mathrm {ex}(n,Q_d)=O_d(n^{2-1/d})$. A recent general result of Sudakov and Tomon implies the slightly stronger bound 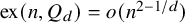$\mathrm {ex}(n,Q_d)=o(n^{2-1/d})$. We obtain the first power-improvement for this old problem by showing that 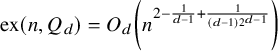$\mathrm {ex}(n,Q_d)=O_d\left (n^{2-\frac {1}{d-1}+\frac {1}{(d-1)2^{d-1}}}\right )$. This answers a question of Liu. Moreover, our techniques give a power improvement for a larger class of graphs than cubes.

We use a similar method to prove that any n-vertex, properly edge-coloured graph without a rainbow cycle has at most 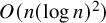$O(n(\log n)^2)$ edges, improving the previous best bound of 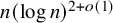$n(\log n)^{2+o(1)}$ by Tomon. Furthermore, we show that any properly edge-coloured n-vertex graph with 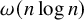$\omega (n\log n)$ edges contains a cycle which is almost rainbow: that is, almost all edges in it have a unique colour. This latter result is tight.

The aim of this paper is to study supersoluble skew braces, a class of skew braces that encompasses all finite skew braces of square-free order. It turns out that finite supersoluble skew braces have Sylow towers and that in an arbitrary supersoluble skew brace B many relevant skew brace-theoretical properties are easier to identify: For example, a centrally nilpotent ideal of B is B-centrally nilpotent, a fact that simplifies the computational search for the Fitting ideal; also, B has finite multipermutational level if and only if $(B,+)$ is nilpotent.

Given a finite presentation of the structure skew brace $G(X,r)$ associated with a finite nondegenerate solution of the Yang–Baxter equation (YBE), there is an algorithm that decides if $G(X,r)$ is supersoluble or not. Moreover, supersoluble skew braces are examples of almost polycyclic skew braces, so they give rise to solutions of the YBE on which one can algorithmically work on.

Many problems and conjectures in extremal combinatorics concern polynomial inequalities between homomorphism densities of graphs where we allow edges to have real weights. Using the theory of graph limits, we can equivalently evaluate polynomial expressions in homomorphism densities on kernels W, that is, symmetric, bounded and measurable functions W from $[0,1]^2 \to \mathbb {R}$. In 2011, Hatami and Norin proved a fundamental result that it is undecidable to determine the validity of polynomial inequalities in homomorphism densities for graphons (i.e., the case where the range of W is $[0,1]$, which corresponds to unweighted graphs or, equivalently, to graphs with edge weights between $0$ and $1$). The corresponding problem for more general sets of kernels, for example, for all kernels or for kernels with range $[-1,1]$, remains open. For any $a> 0$, we show undecidability of polynomial inequalities for any set of kernels which contains all kernels with range $\{0,a\}$. This result also answers a question raised by Lovász about finding computationally effective certificates for the validity of homomorphism density inequalities in kernels.