The modern algebraic treatment of geometry in projective spaces focuses attention on the properties of homogeneous ideals in polynomial and power-series rings. This inevitably raises questions concerning how far ordinary ideal theory needs to be modified if only homogeneous ideals are to be regarded as significant. In practice, one can usually answer any particular question of this type without undue difficulty when it arises but, it seems to the author, the topic has enough intrinsic interest to merit a connected discussion by itself.

The main result in this paper, contained in Theorem 1, is a generalisation of the inequality of the arithmetic-geometric means. A result of a similar character has been proved by Siegel (2). The present result gives an improvement in the inequality in the case when the variables involved are not all distinct, whereas Siegel's result does not. The theorem is used in § 3 to obtain a result in connection with totally real and positive algebraic integers.

In this paper I construct a reduction formula for the integral

the formula connects any three consecutive members of a set I0, I1, I2, …, Im. We regard m as given, and, in order to avoid wasting time over trivialities, we postulate that the constants a, α, β, γ δ (which are not restricted to be real) have real parts large enough to ensure (i) that the integrals In under consideration and the integrals related to them which will be introduced subsequently are all absolutely convergent, and (ii) that, in all the partial integrations which will be effected, the integrated parts vanish at both limits.

There are some simple facts which distinguish Lie-algebras over fields of prime characteristic from Lie-algebras over fields of characteristic zero. These are

(1) The degrees of the absolutely irreducible representations of a Lie-algebra of prime characteristic are bounded whereas, according to a theorem of H. Weyl, the degrees of the absolutely irreducible representations of a semi-simple Lie-algebra over a field of characteristic zero can be arbitrarily high.

(2) For each Lie-algebra of prime characteristic there are indecomposable representations which are not irreducible, whereas every indecomposable representation of a semi-simple Liealgebra over a field of characteristic zero is irreducible (cf. [4]).

(3) The quotient ring of the embedding algebra of a Lie-algebra over a field of prime characteristic is a division algebra of finite dimension over its center, whereas this is not the case for characteristic zero. (cf. [4]).

(4) There are faithful fully reducible representations of every Lie-algebra of prime characteristic, whereas for characteristic zero only ring sums of semi-simple Lie-algebras and abelian Lie-algebras admit faithful fully reducible representations (cf. [6], [2], [4]).

In a paper published recently in this Journal, Watson obtained a reduction formul for the integral

He showed that this reduction formula could be written in the form:

If

then

where

and 2σ = α + β + γ + δ, 2θ3 = α − β − γ + δ.

The object of this note is to construct a set of real three-dimensional Lie groups such that every real three-dimensional Lie group is locally isomorphic with some group in the set. The construction is effected by first finding canonical forms for the constants of structure of real three-dimensional Lie algebras; these canonical forms give rise to certain bilinear forms, and the Lie groups are obtained as linear groups isomorphic with groups of automorphisms which leave these bilinear forms invariant.

Let μ be a homomorphic mapping of some subgroup A of the group G onto a subgroup Ḃ (not necessarily distinct from A) of G; then we call μ a partial endomorphism of G. If A coincides with G, that is, if the homomorphism is defined on the whole of G, we speak of a total endomorphism; this is what is usually called an endomorphism of G. A partial (or total) endomorphism μ*extends or continues a partial endomorphism μ if the domain of μ* contains the domain of μ, that is, μ* is defined for (at least) all those elements for which μ. is defined, and moreover μ* coincides with μ where μ is defined.

The development of the theory of local rings has been greatly stimulated by the importance of the applications to algebraic geometry, but it is none the less true that this stimulus has produced a theory which, on aesthetic grounds, is somewhat unsatisfactory. In the first place, if a local ring Q arises in the ordinary way from a geometric problem, then Qwill have the same characteristic as its residue field. It is partly for this reason that our knowledge of equicharacteristic local rings is much more extensive than it is of those local rings which present the case of unequal characteristics. Again, in the geometric case, the integral closure of Q in its quotient field will be a finite Q-module. Here, once more, we have a special situation which it would be desirable to abandon from the point of view of a general abstract theory.

Groups that can be represented as the product of two proper subgroups have been studied extensively; one of the latest contributions is a paper by Wielandt (8), in which references to previous work can be found. In the case where the two proper subgroups have only the unit element in common, we adopt the term ‘general product’introduced by Neumann (1).

Let G be a finite group, H an arbitrary subgroup (i.e., not necessarily normal); we decompose G as a union of left cosets modulo H:

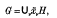
choosing fixed coset representatives 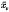v. In this paper we construct a “coset space complex” and assign cohomology groups; Hr([G: H], A), to it for all coefficient modules A and all dimensions, -∞<r<∞. We show that if

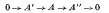
is an exact sequence of coefficient modules such that H1U, A')= 0 for all subgroups U of H, then a cohomology group sequence

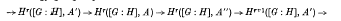
may be defined and is exact for -∞<r<∞. We also provide a link between the cohomology groups Hr([G: H], A) and the cohomology groups of G and H; namely, we prove that if Hv(U, A)= 0 for all subgroups U of H and for v = 1, 2, …, n–1, then the sequence

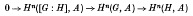
is exact, where the homomorphisms of the sequence are those induced by injection, inflation and restriction respectively.

The object of this paper is to evaluate a few infinite integrals involving E-functions by applying the Parseval-Goldstein [1] theorem of Operational Calculus; that, if

and

then

when the integrals are convergent.

In a previous paper [5] the equivalence of randomisation and normal theory distributions of linear combinations was discussed. In the present paper we discuss the asymptotic randomisation distributions of statistics used in analysis of variance and in a closely related problem which includes, in particular, the “problem of m-rankings“. Kruskal [4] has studied the first of these questions in the case where observations are replaced by ranks.

The formulae to be proved are

where m is a positive integer, p ≧ q + 1, R(mar + k) > 0, r = 1, 2, …, p, and | amp z |ππ. For other values of p and q the result holds if the integral is convergent.

The formula to be proved is

In proving (1) the following formulae are required:

where p≥q + 1, (1).

The two following formulae are to be established.

If R (m ± n) > 0, | amp z | < π,

If p ≧ q + 1, R(k ± n + 2αr) > 0, r = 1, 2, …, p, | amp z | < π,

For other values of p and q the formula holds if the integral is convergent.

In this paper we prove a theorem in Operational Calculus and use it to evaluate a few infinite integrals involving Legendre, Bessel and E-functions. We write

when

and

when

(2) is a generalisation of (1) as given by Meijer [2] and it reduces to (1) when v = ±½ by virtue of the relation

The formula to be proved is

where R(z)>0.

The first formula to be proved is

where R(z)>0.

The formulae to be proved are as follows.

If p ≧ q + 1, R(l + m) > 0, R(αr − l − m + n)> −1, R(αr − l − m − n)> 0, r = 1,2,…p,

If p ≧ q + 1, R(l >0, R(l+m >0, R(αr − l − m + n)> −1,