The discrepancies between observed and theoretically calculated period ratios of the double mode, classical Cepheids and other groups of Cepheid type variables have played a prominent role in investigations of the important physical characteristics of these stars during the last twenty years. Today, there is growing consensus that the drastic increases in astrophysical opacities proposed by Simon (1982) provide the correct solution of all the period ratio problems (e.g. Petersen, 1989; Iglesias and Rogers, 1992; Moskalik et al., 1991).

It seems at first strange that the optimal opacity change (see Andreasen, 1988) can produce both the decrease in period ratio for double mode classical Cepheids and the increased period ratio in models of δ Scuti stars. Here we use ĸ-effect-functions (Refsdal and Stabell, 1972) to provide both a detailed description of the effects of opacity changes and an improved and more direct understanding of these effects.

The application of Fourier decomposition parameters has revolutionized important areas of investigations of Cepheid type variables since the introduction of Fourier analysis in its modern form by Simon and Lee (1981).

In the literature several different representations of the results of Fourier analysis have been utilized. In view of the growing interest for applications of Fourier decomposition it is important to use and publish Fourier data in an optimal way. Most studies until now have used amplitude ratios and phase differences derived from traditional light curves giving the light variation in magnitudes, following the original recipe of Simon and Lee (1981). However, Stellingwerf and Donohoe (1986) advocated the use of phases rather than phase differences. Recently, Buchler et al. (1990) argued that the standard Simon & Lee form contains all relevant physics, and suggested analysis of flux-values rather than of magnitudes, because this removes the distorting effects of constant, false light. Thus there are many choices to be made in practical applications of Fourier analysis, and there is at present no convincing argument for preferring one specific representation.

In this report the results of spectroscopic observations on selected F supergiant stars as the candidates of proto-planetary nebulae (PPNs) are presented. Volk and Kwok(1989) selected nearly one hundred new candidates of PPNs based upon the scenario on the evolution of them. They summarized four classes of stars which should be the PPNs and are described in various papers. These are (i) High galactic latitude supergiants, (ii) Nonvariable OH/IR stars, (iii) Low color temperature infrared objects, and (iv) R. CrB. In order to examine the extended envelope of the PPNs we have started our project to obtain the Hα profile which should give us some clue to the structure of the envelope. We are mainly concerned with F supergiant stars. Our sample objects are mostly classified as pulsating or semiregular variables.

Rapid progress in the stellar pulsation research has presented many new challenges to traditional pulsation theory. The following progress made by us should belong to one of the new challenges:

1. 1) There are many variable stars located at the Horizontal Branch (HB) but outside the instability strip with amplitude larger than 0.02 mag.

Maybe some astronomers have already doubted of the 1950’s conclusion-the RR Lyrae stars are confined to the narrow instability strip in the C-M diagram, the boundaries of the gap are extremely sharp and definite, beyond the edges no light variations occur with ranges greater than 0.02 mag. We are changing the conclusion by observations. Here we do not mean the microvariability. We still raise the question from the classical viewpoint. We want to show that there are variable stars outside the strip with peak to peak amplitudes larger than 0.02 mag.

The life-time of the star on AGB is approximately 6 × 104 yr. We divide it into front half and back half of AGB (including to optical Mira variable and OH/IR star) according to their evolution character. The observations show that the star has non-pulsation, but constant mass loss rate (~ 5 × 10−7M⊙ yr−1) on front half of AGB. Its circumstellar envelope is formed. When the star has pulsation on back half of AGB, its mass loss rate is relative with time, and increases gradually. In this time the star is on the stage of optical Mira variable. When the mass loss rate reaches the value of ~ 3 × 10−6M⊙ yr−1, the star evoluted from the stage of optical variable into the stage of radio bright OH/IR star. On the end of AGB the mass loss rate reaches ~10−4M⊙ yr−1. (Band and Habing 1983, Hermen and Habing 1985).

We can find the conclusion with our analysis for VLA observation of OH maser and CO (2–1) emission line that they are distributed on some different distinct shells in the circumstellar envelope, respectively.

On short time-scales of under a year, the vast majority of δ Scuti stars studied in detail show completely regular multiperiodic pulsation. Nonradial pulsation is characterized by the excitation of a large number of modes with small amplitudes. Reports of short-term irregularity or nonperiodicity in the literature need to be examined carefully, since insufficient observational data can lead to an incorrect impression of irregularity. Some interesting cases of reported irregularities are examined.

A few δ Scuti stars, such as 21 Mon, have shown stable variations with sudden mode switching to a new frequency spectrum. This situation might be an indication of deterministic chaos. However, the observational evidence for mode switching is still weak.

One the other hand, the case for the existence of long-term amplitude and period changes is becoming quite convincing. Recently found examples of nonradial pulsators with long-term changes are 4 CVn, 44 Tau, τ Peg and HD 2724. (We note that other δ Scuti pulsators such as X Cae and θ2 Tau, have shown no evidence for amplitude variations over the years.) Neither the amplitude nor the period changes are periodic, although irregular cycles with time scales between a few and twenty years can be seen. While the amplitude changes can be very large, the period changes are quite small. This property is common in nonlinear systems which lead to chaotic behavior. There exists observational evidence for relatively sudden period jumps changing the period by about 10−5 and/or slow period changes near dP/dt ≤ 10−9. These period changes are an order of magnitude larger than those expected from stellar evolution.

The nonperiodic long-term changes are interpreted in terms of resonances between different nonradial modes. It is shown that a large number of the nonradial acoustic modes can be in resonance with other modes once the mode interaction terms, different radial orders and rotational m-mode splitting are considered. These resonances are illustrated numerically by the use of pulsation model. Observational evidence is presented that these interaction modes exist in the low-frequency domain.

Target of a STEPHI multisite campaign, the Delta Scuti star GX Pegasi has been found to oscillate with at least five simultaneous, close frequencies (table I).

Mode identification together with informations about the star that such an identification can provide are outlined below (see also Michel et al, 1992b).

The mode identification is carried out by means of a comparison between the observed frequencies and the adiabatic frequencies of models appropriate to this star. Models that match GX Peg’s position in a Hertzsprung-Russell diagram have masses in the range 1.9 – M⊙. When included, convective core overshoot is handled as in Maeder and Meynet (1989). According to these models, GX Peg is a rather evolved, main sequence star.

Using unpublished data obtained in 1982 at Mexico and Turkey combined with Hungarian observations the process of amplitude variation of the frequency at 18.5 c/d is shown. The time scale of the amplitude increase is less than 100 days.

The Short periods of Delta Scuti Stars allow the observational detection of the period changes expected from the stellar evolution within several tens years. For about 30 years we are keeping this topic as a small systematic observational program with our 60 cm telescope. Here we publish the period variation of 18 stars in table I. The data of 28 And are taken from R. Garrido et al. in AAp 144 (1983), 211; the period variation rate of 4 CVn is given by M. Breger. Both of them are low amplitude variables.

From these data we find out that both the population I and II variables can have period increasing and decreasing. The rate is between 2 × 10−6 to 8 × 10−8 days/year. Due to the period range of about 0.2 days, the time scale of period variation in one direction is limited within about 2 million to 200 million years. Usually we take the mass of this A to F type variables as 1.5 to 2.0 solar mass, so the main sequence life time is about several billion years. If all these A to F type main sequence stars will be variable in some period of its life time the possibility for a star to show Delta Scuti type variation is about hundredth, especially for the high amplitude type. Up to now we have found some 50 high amplitude variables with V < 10.5, and the total number of A3 to F5 with V < 10.5 is about 1.2 × 105, so the incidence of high amplitude variables is about 0.04%.

The measurements of uvby Hβ of HD 93044 were obtained in April 1991. and the observational results that the star locates nearly in the middle of δ Scuti instability strip with somewhat deviation to red edge. According to Crawford (1979) and Philip’s (1979) calibrations, the effective temperature, absolute visual magnitude and surface gravity are obtained to be Teff = 7300±200 K, Mv = l.m33±0.39 and logg = 3.7±0.15, respectively. The observational results of Δmi = 0.01 give an estimate of [Fe/H] = —0.003 ± 0.18, so the opinion of metallic deficient is not supported obviously. The observations show the reddening index E(b — y) to be 0.014 which is 1.4 times as large as the standard deviation of Crawford’s (1979) statistics.

HD93044 was observed electrophotometricaly on April 21, May 1, 2 and 4, 1991 at Xinglong Station of Beijing Astronomical Observatory. Combining the data with Li Zhiping’s data together and a period analysis was completed using a program which consists of a combination of Fourier transforms of prewhitened data and the multifrequency least squares of brightness residuals (LSR). Three pulsation frequencies (11.90809, 16.79553, 22.44827 cycles per day) with visual amplitudes between 0.0056 and 0.0203 mag were found. The solution fits the observations to +0.0071 mag which is equal to the mean square deviation of observations. The first frequency (11.90809 cycles per day) must be the right value of the fundamental frequency of HD93044.

The ZZ Ceti stars form a class of variable white dwarfs: the hydrogen dominated atmosphere ones, which do pulsate in an instability strip in the effective temperature range 13000K-11500K. We know 22 such ZZ Ceti white dwarfs. Their variations are caused by nonradial g-mode pulsations with periods are in the range 100-1000 seconds.

A subsample of the ZZ Ceti stars shows amplitude variations on time scales of the order of one month. These variations could be driven by nonlinear phenomena.

To examine the non-linear oscillation and period change of white dwarf variables, ZZ Psc is discussed observationally. As a result of data reduction we found two major periods, 680 seconds and 860 seconds, but could not find chaotic behavior of ZZ Psc.

The rapidly oscillating Ap stars pulsate in high-overtone, low degree p-modes with their pulsation axes aligned with their oblique magnetic axes. They show non-linearity in their pulsation in three ways:

1. 1) The harmonics of the basic pulsation frequency are detectable.

2. 2) The pulsation phase seems to vary stochastically on a time scale of days to years depending on the star.

3. 3) The form of the nonradial surface distortion is not constant with time.

These three effects are illustrated with HR 3831, the best studied of the roAp stars. HR 3831 pulsates in distorted dipole mode which can be modelled as a linear sum of axisymmetric l = 0, 1, 2, and 3 spherical harmonics aligned with the magnetic axis. This gives rise to a 7-frequency multiplet split by exactly the rotation frequency. The form of the distortion shows small changes on a time-scale of years. HR 3831 shows a 5-frequency rotationally split first harmonic multiplet, a 3-frequency rotationally split second harmonic multiplet, and a single third harmonic frequency has probably been detected at an amplitude of 0.065 mmag. The first harmonic has changed its form significantly over the last 10 years. A technique for decomposing the fundamental frequency septuplet into its component spherical harmonics is used to fit the pulsation phase as a function of rotation phase. This allows a unique O-C to be defined for any length of light curve. The long term behaviour of the O-C diagram cannot be modelled adequately with a combination of periodic (Doppler shift) and quadratic (evolution) terms; there seems to be a significant stochastic component. The direction of the pulsation phase reversal at rotational phase 0.747 is indeterminate; sometimes it is a positive-going reversal, sometimes negative-going. At present it is not known whether this is a numerical artifact, or a physical effect in the star. If it is a physical effect, it means that small non-periodic differences in pulsation amplitude between the bipolar hemispheres have been detected.

Due to the large fluctuation of the time of light maxima, in each observational season only very few observations is very dangerous for period variation research. Especially when the observation is not accurate enough such as for the early radial velocity data. Of course parts of the fluctuation are real which are caused by the chaotic behavior of the complicated pulsation. Generally the pulsation is quite periodic but is not like a timer such as the oscillation of the quartz or the rotating of the pulsar, all of these as much simple.

The period increasing rate of BW Vul from our results is 0.34 micron days per year which makes a evolution time scale about 3 million years. For a star with mass of 10 solar mass, the life age on the main sequence is about 10 million years. So BW Vul should not be very far away from the main sequence.

The line-profile variations have been found in many early-type stars surrounding the classical β Cephei variables in the H-R diagram. The feature of the variations has not been known enough mainly because of their periods of about one day. To specify the cause of the variations, however, it is necessary to make clear their features such as the multi-periodicity, the relation between the photometric variations and the spectroscopic ones, and the cause of existence or non-existence of mode (or period) switching (Balona 1991, Smith 1991). In Be stars, the correlation of the amplitude of the variations with their emission cycle is also important (Ando 1986).

We present some evidence of the quasi-periodic long-term variations (QPLV) in the violet-to-red ratio of double-peaked emission lines (V/R variation) and/or in the radial velocities of shell absorption lines for some Be stars. Although the V/R variations are rather prevailing phenomena among Be stars, the QPLV is remarkable by the following characteristics:

1. (1) The QPLV appears as a sudden onset of repeated V/R variations after a long (10 years), almost stable period, and it persists for a few or several periods in ten or more years.

2. (2) The period and amplitude of V/R variations change from cycle to cycle and from star to star. The variations of radial velocities (RV) of shell absorption lines are usually nearly parallel with the V/R variations.

3. (3) The QPLV appears usually in early type Be stars with large rotational velocities, regardless whether the stars are normal Be or shell stars, and whether they are close-binaries or single stars.

The results are presented of multi-channel photometry and spectroscopy of the suspected nova-like variable FY Per. These results suggest that FY Per may be a Herbig Ae/Be star rather than a nova-like variable.

Efficient tools of investigation of stellar pulsation are the integral relations which link oscillation frequencies to the static structure of stellar models, as provided by the linear theory of pulsation (for a review, see Saio, this conference).

Similarly, oscillation amplitudes and phases, which arise from nonlinear processes, can be related to the stellar structure by means of amplitude equation formalisms (for a review, see Buchler, this conference).

For the simple case of a monoperiodic oscillation, involving only one unstable marginal mode, such a formalism shows that the (limit cycle) radius variations, at time t and mass level m, can be approximated, up to second order of approximation, (Buchler and Goupil, 1984; Buchler and Kovàca, 1986) by:

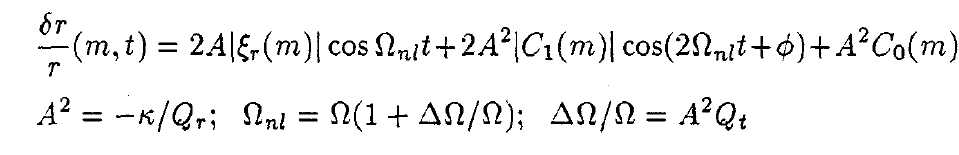
where A, R, Ω, ĸ, £r(m) respectively are the amplitude, stellar radius, linear nonadiabatic frequency, growth rate, radius eigenfunction. Second order nonlinearities generated first harmonic oscillations and change in equilibrium radius about which the star oscillates, as represented by the last two terms in (la) respectively. Analogous expressions are obtained for velocity and light variations, that can be compared with observations.