We consider Gaussian approximation in a variant of the classical Johnson–Mehl birth–growth model with random growth speed. Seeds appear randomly in $\mathbb{R}^d$ at random times and start growing instantaneously in all directions with a random speed. The locations, birth times, and growth speeds of the seeds are given by a Poisson process. Under suitable conditions on the random growth speed, the time distribution, and a weight function $h\;:\;\mathbb{R}^d \times [0,\infty) \to [0,\infty)$, we prove a Gaussian convergence of the sum of the weights at the exposed points, which are those seeds in the model that are not covered at the time of their birth. Such models have previously been considered, albeit with fixed growth speed. Moreover, using recent results on stabilization regions, we provide non-asymptotic bounds on the distance between the normalized sum of weights and a standard Gaussian random variable in the Wasserstein and Kolmogorov metrics.

Gaussian process regression is widely used to model an unknown function on a continuous domain by interpolating a discrete set of observed design points. We develop a theoretical framework for proving new moderate deviations inequalities on different types of error probabilities that arise in GP regression. Two specific examples of broad interest are the probability of falsely ordering pairs of points (incorrectly estimating one point as being better than another) and the tail probability of the estimation error at an arbitrary point. Our inequalities connect these probabilities to the mesh norm, which measures how well the design points fill the space.

Let $(\xi_k,\eta_k)_{k\in\mathbb{N}}$ be independent identically distributed random vectors with arbitrarily dependent positive components. We call a (globally) perturbed random walk a random sequence $T\,{:\!=}\, (T_k)_{k\in\mathbb{N}}$ defined by $T_k\,{:\!=}\, \xi_1+\cdots+\xi_{k-1}+\eta_k$ for $k\in\mathbb{N}$ . Consider a general branching process generated by T and let $N_j(t)$ denote the number of the jth generation individuals with birth times $\leq t$ . We treat early generations, that is, fixed generations j which do not depend on t. In this setting we prove counterparts for $\mathbb{E}N_j$ of the Blackwell theorem and the key renewal theorem, prove a strong law of large numbers for $N_j$ , and find the first-order asymptotics for the variance of $N_j$ . Also, we prove a functional limit theorem for the vector-valued process $(N_1(ut),\ldots, N_j(ut))_{u\geq0}$ , properly normalized and centered, as $t\to\infty$ . The limit is a vector-valued Gaussian process whose components are integrated Brownian motions.

The Dagum family of isotropic covariance functions has two parameters that allow for decoupling of the fractal dimension and the Hurst effect for Gaussian random fields that are stationary and isotropic over Euclidean spaces. Sufficient conditions that allow for positive definiteness in $\mathbb{R}^d$ of the Dagum family have been proposed on the basis of the fact that the Dagum family allows for complete monotonicity under some parameter restrictions. The spectral properties of the Dagum family have been inspected to a very limited extent only, and this paper gives insight into this direction. Specifically, we study finite and asymptotic properties of the isotropic spectral density (intended as the Hankel transform) of the Dagum model. Also, we establish some closed-form expressions for the Dagum spectral density in terms of the Fox–Wright functions. Finally, we provide asymptotic properties for such a class of spectral densities.

Gromov–Wasserstein distances were proposed a few years ago to compare distributions which do not lie in the same space. In particular, they offer an interesting alternative to the Wasserstein distances for comparing probability measures living on Euclidean spaces of different dimensions. We focus on the Gromov–Wasserstein distance with a ground cost defined as the squared Euclidean distance, and we study the form of the optimal plan between Gaussian distributions. We show that when the optimal plan is restricted to Gaussian distributions, the problem has a very simple linear solution, which is also a solution of the linear Gromov–Monge problem. We also study the problem without restriction on the optimal plan, and provide lower and upper bounds for the value of the Gromov–Wasserstein distance between Gaussian distributions.

In this paper we analyze a simple spectral method (EIG1) for the problem of matrix alignment, consisting in aligning their leading eigenvectors: given two matrices A and B, we compute two corresponding leading eigenvectors $v_1$ and 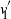$v'_{\!\!1}$ . The algorithm returns the permutation 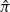$\hat{\pi}$ such that the rank of coordinate 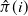$\hat{\pi}(i)$ in 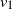$v_1$ and that of coordinate i in 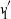$v'_{\!\!1}$ (up to the sign of 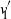$v'_{\!\!1}$ ) are the same.

We consider a model of weighted graphs where the adjacency matrix A belongs to the Gaussian orthogonal ensemble of size 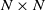$N \times N$ , and B is a noisy version of A where all nodes have been relabeled according to some planted permutation 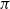$\pi$ ; that is, 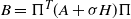$B= \Pi^T (A+\sigma H) \Pi $ , where 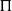$\Pi$ is the permutation matrix associated with 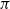$\pi$ and H is an independent copy of A. We show the following zero–one law: with high probability, under the condition 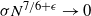$\sigma N^{7/6+\epsilon} \to 0$ for some 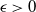$\epsilon>0$ , EIG1 recovers all but a vanishing part of the underlying permutation 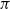$\pi$ , whereas if 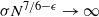$\sigma N^{7/6-\epsilon} \to \infty$ , this method cannot recover more than o(N) correct matches.

This result gives an understanding of the simplest and fastest spectral method for matrix alignment (or complete weighted graph alignment), and involves proof methods and techniques which could be of independent interest.

For a non-negative separable random field Z(t), $t\in \mathbb{R}^d$ , satisfying some mild assumptions, we show that $ H_Z^\delta =\lim_{{T} \to \infty} ({1}/{T^d}) \mathbb{E}\{{\sup_{ t\in [0,T]^d \cap \delta \mathbb{Z}^d } Z(t) }\} <\infty$ for $\delta \ge 0$ , where $0 \mathbb{Z}^d\,:\!=\,\mathbb{R}^d$ , and prove that $H_Z^0$ can be approximated by $H_Z^\delta$ if $\delta$ tends to 0. These results extend the classical findings for Pickands constants $H_{Z}^\delta$ , defined for $Z(t)= \exp( \sqrt{ 2} B_\alpha (t)- \lvert {t} \rvert^{2\alpha })$ , $t\in \mathbb{R}$ , with $B_\alpha$ a standard fractional Brownian motion with Hurst parameter $\alpha \in (0,1]$ . The continuity of $H_{Z}^\delta$ at $\delta=0$ is additionally shown for two particular extensions of Pickands constants.

Motivated by mathematical tissue growth modelling, we consider the problem of approximating the dynamics of multicolor Pólya urn processes that start with large numbers of balls of different colors and run for a long time. Using strong approximation theorems for empirical and quantile processes, we establish Gaussian process approximations for the Pólya urn processes. The approximating processes are sums of a multivariate Brownian motion process and an independent linear drift with a random Gaussian coefficient. The dominating term between the two depends on the ratio of the number of time steps n to the initial number of balls N in the urn. We also establish an upper bound of the form $c(n^{-1/2}+N^{-1/2})$ for the maximum deviation over the class of convex Borel sets of the step-n urn composition distribution from the approximating normal law.

By a general shot noise process we mean a shot noise process in which the counting process of shots is arbitrary locally finite. Assuming that the counting process of shots satisfies a functional limit theorem in the Skorokhod space with a locally Hölder continuous Gaussian limit process, and that the response function is regularly varying at infinity, we prove that the corresponding general shot noise process satisfies a similar functional limit theorem with a different limit process and different normalization and centering functions. For instance, if the limit process for the counting process of shots is a Brownian motion, then the limit process for the general shot noise process is a Riemann–Liouville process. We specialize our result for five particular counting processes. Also, we investigate Hölder continuity of the limit processes for general shot noise processes.