We investigate wind wave growth by direct numerical simulations solving for the two-phase Navier–Stokes equations. We consider the ratio of the wave speed $c$ to the wind friction velocity $u_*$ from $c/u_*= 2$ to 8, i.e. in the slow to intermediate wave regime; and initial wave steepness $ak$ from 0.1 to 0.3; the two being varied independently. The turbulent wind and the travelling, nearly monochromatic waves are fully coupled without any subgrid-scale models. The wall friction Reynolds number is 720. The novel fully coupled approach captures the simultaneous evolution of the wave amplitude and shape, together with the underwater boundary layer (drift current), up to wave breaking. The wave energy growth computed from the time-dependent surface elevation is in quantitative agreement with that computed from the surface pressure distribution, which confirms the leading role of the pressure forcing for finite amplitude gravity waves. The phase shift and the amplitude of the principal mode of surface pressure distribution are systematically reported, to provide direct evidence for possible wind wave growth theories. Intermittent and localised airflow separation is observed for steep waves with small wave age, but its effect on setting the phase-averaged pressure distribution is not drastically different from that of non-separated sheltering. We find that the wave form drag force is not a strong function of wave age but closely related to wave steepness. In addition, the history of wind wave coupling can affect the wave form drag, due to the wave crest shape and other complex coupling effects. The normalised wave growth rate we obtain agrees with previous studies. We make an effort to clarify various commonly adopted underlying assumptions, and to reconcile the scattering of the data between different previous theoretical, numerical and experimental results, as we revisit this longstanding problem with new numerical evidence.

Interactions between shock waves and boundary layers produce flow separations and augmented pressure/thermal loads in hypersonic flight. This study provides details of Mach 7 impinging-shock-flat-plate experiments conducted in the T4 Stalker Tube. Measurements were taken at flow conditions of Mach 7.0 (2.44 MJ kg$^{-1}$) and Mach 7.7 (2.88 MJ kg$^{-1}$) flight enthalpies with a range of freestream unit Reynolds numbers from $1.43 \times 10^{6}$ m$^{-1}$ to $5.01 \times 10^{6}$ m$^{-1}$. A shock generator at $12^{\circ }$ or $16^{\circ }$ to the freestream created an oblique shock which impinged on a boundary layer over a flat plate to induce flow separation. The flow field was examined using simultaneous measurements of wall static pressure, heat transfer and schlieren visualisation. Measured heat transfer along the flat plate without the shock impingement indicated that the boundary layer remained laminar for all flow conditions. The shock impingement flow field was successfully established within the facility test duration. The onset of separation was observed by a rise in wall pressure and a decrease in heat transfer at the location corresponding to the stem of the separation shock. Downstream of this initial rise, an increased pressure and higher heating loads were observed. The heat-transfer levels also indicated an immediate boundary layer transition due to the shock impingement. The separation data of the present work showed good agreement with our previous work on shock impingement on heated walls (Chang et al., J. Fluid Mech., vol. 908, 2021, pp. 1–13). A comparison with the previous scaling indicated that the separation also relates to the pressure ratio and the wall temperature parameter.

This paper addresses several aspects of the axisymmetric flow of a liquid film over the surface of a downward-sloping cone. The study is rooted on a validated computational tool the results of which are interpreted with the help of a hyperbolic time-dependent reduced-order model also derived in the paper. The steady version of the model demonstrates the weakening and ultimate disappearance of the circular hydraulic jump as the cone surface transitions from planar to downward sloping. Mathematically, this evolution is reflected in a change of the model's critical point from spiral to node. A significant advantage of the time-dependent model is that, when it is integrated in time, the flow regions upstream and downstream of the critical point are connected. Due to this feature, when a hydraulic jump exists, its position can be sharply captured automatically with a good agreement with Navier–Stokes simulations. Surface-tension effects are properly accounted for and, in steady conditions, are shown to have a marginal effect on the flow, including the position of the hydraulic jump. A correlation is obtained for the jump radius as a function of the flow rate, liquid viscosity, gravitational acceleration and the angle of inclination of the cone surface. In a suitable limit, the model reduces to the optimal two-dimensional, first-order model for liquid film flow down an inclined plane and, in a different limit, it describes an axisymmetric thin liquid film falling down the surface of a vertical cylinder. Some results are also presented for the waves induced by a pulsating jet on the surface of the liquid film and for a jet impinging on the surface of a cone from below.

We investigate the local self-sustained process underlying spiral turbulence in counter-rotating Taylor–Couette flow using a periodic annular domain, shaped as a parallelogram, two of whose sides are aligned with the cylindrical helix described by the spiral pattern. The primary focus of the study is placed on the emergence of drifting–rotating waves (DRW) that capture, in a relatively small domain, the main features of coherent structures typically observed in developed turbulence. The transitional dynamics of the subcritical region, far below the first instability of the laminar circular Couette flow, is determined by the upper and lower branches of DRW solutions originated at saddle-node bifurcations. The mechanism whereby these solutions self-sustain, and the chaotic dynamics they induce, are conspicuously reminiscent of other subcritical shear flows. Remarkably, the flow properties of DRW persist even as the Reynolds number is increased beyond the linear stability threshold of the base flow. Simulations in a narrow parallelogram domain stretched in the azimuthal direction to revolve around the apparatus a full turn confirm that self-sustained vortices eventually concentrate into a localised pattern. The resulting statistical steady state satisfactorily reproduces qualitatively, and to a certain degree also quantitatively, the topology and properties of spiral turbulence as calculated in a large periodic domain of sufficient aspect ratio that is representative of the real system.

The motion of Taylor bubbles in capillaries is typical of many engineering and biological systems, ranging from subsurface flows to small-scale reactors. Although the hydrodynamics of elongated bubbles has been the object of several studies, the case where a solute is transported in the surrounding liquid and surface mass-transfer mechanisms act on the solid wall or the bubble–fluid interface is much less understood. To fill this gap, we investigate the transport problem around a confined Taylor bubble to access the competition between advection, diffusion and surface mass transfer in the different regions of the bubble. With this aim, we derive a one-dimensional advection–diffusion–mass-transfer equation where the transport mechanisms are described through an effective velocity, an effective diffusion coefficient and an effective Sherwood number. Our model generalises the Aris–Taylor dispersion to the case of a Taylor bubble and clarifies the impact of surface mass transfer in the advection and diffusion dominated regimes for both the front and rear menisci. The model recovers the typical Pèclet square relationship of the effective diffusion coefficient, which also depends on the film thickness. Also, when the Pèclet number balances with the Sherwood number, there exist conditions that lead to the formation of hot spots of concentration. We show that the typical shape oscillations of the bubble rear locally enhance superficial mass transfer. Finally, we study the transport problem in the uniform film region where the concentration field can be found analytically.

Resonant response of water waves in a narrow gap, the so-called gap resonance, is a hydrodynamic phenomenon with practical applications. When coupled to body motions, the physics becomes rather complicated, involving body motions, fluid resonance and damping that determines the response amplitude. Gap resonances between two identical elongated bodies, with one held fixed and the other floating, are investigated experimentally for unidirectional waves with broadside incidence. Transient wave groups with different maximum surface elevations are generated, to examine the nonlinear physics. Sub- and super-harmonics, which can be substantially larger than the linear component, are observed in the responses. When going from the diffraction problem (both bodies fixed) to the coupled problem (allowing one body to move), the gap responses are significantly amplified, i.e. by a factor of 2. The first resonant mode that dominates the diffraction problem disappears in the coupled problem. A new resonant mode, which is shown to arise from body motions, is excited inside the gap through nonlinear processes. This mode features a double-humped ‘camel-back’ shape, leading to remarkably large responses. The floating body is observed to oscillate in sway with significant amplitudes at two distinct natural frequencies that are far apart. This is of great interest for the design of mooring lines connecting the two bodies, as it appears to cause resonances at the wave frequencies in addition to the low frequencies. A semi-analytical model is developed to investigate the multiple natural frequencies in sway, yielding further insight into gap resonances.

Dynamos driven by rotating convection in the plane layer geometry are investigated numerically for a range of Ekman number ($E$), magnetic Prandtl number ($Pm$) and Rayleigh number ($Ra$). The primary purpose of the investigation is to compare results of the simulations with previously developed asymptotic theory that is applicable in the limit of rapid rotation. We find that all of the simulations are in the quasi-geostrophic regime in which the Coriolis and pressure gradient forces are approximately balanced at leading order, whereas all other forces, including the Lorentz force, act as perturbations. Agreement between simulation output and asymptotic scalings for the energetics, flow speeds, magnetic field amplitude and length scales is found. The transition from large-scale dynamos to small-scale dynamos is well described by the magnetic Reynolds number based on the small convective length scale, $\widetilde {Rm}$, with large-scale dynamos preferred when $\widetilde {Rm} \lesssim O(1)$. The magnitude of the large-scale magnetic field is observed to saturate and become approximately constant with increasing Rayleigh number. Energy spectra show that all length scales present in the flow field and the small-scale magnetic field are consistent with a scaling of $E^{1/3}$, even in the turbulent regime. For a fixed value of $E$, we find that the viscous dissipation length scale is approximately constant over a broad range of $Ra$; the ohmic dissipation length scale is approximately constant within the large-scale dynamo regime, but transitions to a $\widetilde {Rm}^{-1/2}$ scaling in the small-scale dynamo regime.

The tip vortices shed by two marine propellers are studied, relying on large-eddy simulation, using a cylindrical grid consisting of 5 billion points. A tip-loaded design, featuring winglets at the tips of its blades, is compared against a conventional one at the design advance coefficient and a model-scale Reynolds number equal to 432 000. The tip-loaded propeller achieves improved performance, but produces also more intense tip vortices. The propeller with winglets actually generates two vortices from the tip of each blade, originating at the edge of each winglet and at the junction between the winglets and the blades. They merge at a short distance downstream, within a diameter from the propeller plane. The helical vortices originating from this merging process experience a slower instability, in comparison with the tip vortices in the wake of the conventional propeller, persisting further downstream, due to the weaker shear with the wakes shed by the following blades. The results of the simulations highlight that splitting the single tip vortex of a conventional propeller into two smaller vortices by means of winglets does not imply necessarily the generation of weaker vortices and lower negative peaks of pressure at their core: the geometry of the winglets needs to be carefully optimized to achieve this target.

Numerical studies of dimple and jet formation from a collapsing cavity often model the initial cavity shape as a truncated sphere, mimicking a bursting bubble. In this study, we present a minimal model containing only nonlinear inertial and capillary forces, which produces dimples and jets from a collapsing capillary wave trough. The trough in our simulation develops from a smooth initial perturbation, chosen to be an eigenmode to the linearised 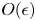${O}(\epsilon )$ problem (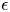$\epsilon$ is the non-dimensional amplitude). We explain the physical mechanism of dimple formation and demonstrate that, for moderate 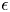$\epsilon$, the sharp dimple seen in simulations is well captured by the weakly nonlinear 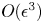${O}(\epsilon ^3)$ theory developed here. For 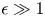$\epsilon \gg 1$ the regime is strongly nonlinear, spreading surface energy into many modes, and the precursor dimple now develops into a sharply rising jet. Here, simulations reveal a novel localised window (in space and time) where the jet evolves self-similarly following inviscid (Keller & Miksis, SIAM J. Appl. Maths, vol. 43, issue 2, 1983, pp. 268–277) scales. We develop an analogy of this regime to a self-similar solution of the first kind, for linearised capillary waves. Our first-principles study demonstrates that, at sufficiently small scales, dimples and jets can form from radial inward focusing of capillary waves, and the formation of this may be described by a relatively simple model employing (nonlinear) inertial and capillary effects. Viscosity and gravity can, however, significantly influence the focusing process, either intensifying the singularity or weakening it (Walls et al., Phys. Rev. E, vol. 92, issue 2, 2015, 021002; Gordillo & Rodríguez-Rodríguez, J. Fluid Mech., vol. 867, 2019, pp. 556–571). This leads, in particular, to critical values of Ohnesorge and Bond numbers, which cannot be obtained from our minimal model.

This study investigates the linear stability of a laminar premixed flame, anchored on a square cylinder and confined inside a channel. Many modern linear analysis concepts have been developed and validated around non-reacting bluff-body wake flows, and the objective of this paper is to explore whether those tools can be applied with the same success to the study of reacting flows in similar configurations. It is found that linear instability analysis of steady reacting flow states accurately predicts critical flow parameters for the onset of limit-cycle oscillations, when compared to direct numerical simulation performed with a simple one-step reaction scheme in the low Mach number limit. Furthermore, the linear analysis predicts a strong stabilising effect of flame ignition, consistent with documented experiments and numerical simulations. Instability in ignited wake flows is, however, found to set in at sufficiently high Reynolds number, and a linear wavemaker analysis characterises this instability as being driven by hydrodynamic mechanisms of a similar nature as in non-reacting wake flows. The frequency of nonlinear limit-cycle flame oscillations in this unstable regime is retrieved accurately by linear eigenmode analysis performed on the time-averaged mean flow, under the condition that the full set of the reacting flow equations is linearised. If, on the contrary, unsteadiness in the density and in the reaction rate are excluded from the linear model, then the congruence between linear and nonlinear dynamics is lost.

The flow under consideration is a wall jet that results from an inclined jet in cross-flow emitted into a zero-pressure-gradient turbulent boundary layer from a slot-like outlet of width $b=0.5\,\mathrm {mm}$ and span $L=20\,\mathrm {mm}$. Despite the finite jet span, the velocity decay and wall-normal spreading rate in the symmetry plane can be described with power laws almost identical to those for the two-dimensional flow determined by Zhou & Wygnanski (AIAA J., vol. 31, 1993, pp. 848–853). This is explained by the lack of significant lateral spreading found in the present configuration due to a self-amplifying inward-directed fluid motion, fundamentally differing from conditions found in the absence of an external stream. Regions with ‘approximately self-similar’ properties also exist in the case of unsteady velocity programmes where the fluid is ejected in a pulsatile fashion. Here, the wall jet is enclosed by a leading vortex structure and a deceleration wave, for which the time-dependent locations can be predicted by means of empirical constants. This yields models for the major properties inside the advancing and diffusing wall jet that only require knowledge regarding the velocity ratio, the ejected momentum flux and the kinematic viscosity, representing an extension to scaling laws for steady wall jets in still ambience established by Narasimha et al. (Aeronaut. Q., vol. 77, 1973, pp. 355–359).

Three-dimensional (3-D) transition in the wake of two tandem co-rotating cylinders is studied numerically for Reynolds numbers $180\le Re\le 500$. Infinite cylinders of equal diameter ($D$) and span ($8D$) are placed at streamwise gaps $Lx=2.5D$ and $7.5D$, and rotated at rotation rates $\alpha =0$, $0.5$, $1$ and $2$. For $\alpha =0$ and $Lx=7.5D$, 3-D transition in the wake of the upstream cylinder resembles that for an isolated cylinder with the formation of Mode-A and Mode-B instabilities, whereas for the downstream cylinder, only Mode-A instability occurs in both the $Lx=2.5D$ and $7.5D$ cases with $\alpha =0$. When the cylinders rotate at $\alpha =1$ for $Lx=7.5D$, staggered transition takes place with the appearance of only Mode-B and only Mode-A instabilities in the near-wake regions of the upstream and downstream bodies, respectively. In the case $Lx=2.5D$, the wake of the rotating cylinders transitions via Mode-C and Mode-D instabilities for $\alpha =0.5$, Mode-D and Mode-D$^\prime$ for $\alpha =1$, and Mode-C and Mode-A for $\alpha =2$. A sudden decrease in near-wake fluctuations, accompanied by a downward jump in the force coefficients, is observed as the 3-D instability shifts from one mode to another, for $\alpha \ge 1$ and $Lx=2.5D$. This discontinuity is caused by the formation of a pair of opposite-signed recirculation zones that mitigate each other's effects in the near-wake region.

We carried out experimental and numerical investigations on the axisymmetric spreading evolution of dynamic spin coating with a single drop of ethanol. The results show that the dynamic spreading process consists of two stages: inertial spreading stage and centrifugal thinning stage. These two stages are connected by a transient state in between characterized by the minimum contact line moving velocity. The Weber number determines the spreading in the first stage, similar to the case of the impact of a drop on a static substrate. The rotational Bond number has a marginal effect on the inertia spreading and the radius at the transient state. In the centrifugal thinning stage, the rotational Bond number dominates the flow while the effect of the Weber number is negligible.

A numerical study on the effect of surface slip on the flow in a constricted channel is presented, with the aim of exploring the use of surface slip to control flow separation. Our focus is on two-dimensional flow in a channel over a bump, with a fixed aspect ratio, upon which a Robin-type slip boundary condition is imposed. When the channel walls are fully no-slip, such a flow is known to develop a region of separation behind the bump, at sufficiently large Reynolds numbers. The effect of slip on the separation bubble dynamics occurring behind the bump is investigated, for Reynolds numbers $2000$ and $4000$. It is shown that surface slip (i) attenuates the intensity of separation as it diminishes the minimum of the streamwise velocity within the recirculation region; (ii) delays the onset of flow separation, shifting it downstream, along the bump, and (iii) reduces the dimensions of the separation bubble behind the bump, allowing the flow to reattach sooner. Ultimately, slip inhibits separation, with both the points of separation and reattachment coalescing, for a slip length $\lambda$ of approximately $0.2$.

We present experiments on large air cavities spanning a wide range of sizes relative to the Hinze scale $d_{H}$, the scale at which turbulent stresses are balanced by surface tension, disintegrating in turbulence. For cavities with initial sizes $d_0$ much larger than $d_{H}$ (probing up to $d_0/d_{H} = 8.3$), the size distribution of bubbles smaller than $d_{H}$ follows $N(d) \propto d^{-3/2}$, with $d$ the bubble diameter. The capillary instability of ligaments involved in the deformation of the large bubbles is shown visually to be responsible for the creation of the small bubbles. Turning to dynamical, three-dimensional measurements of individual break-up events, we describe the break-up child size distribution and the number of child bubbles formed as a function of $d_0/d_{H}$. Then, to model the evolution of a population of bubbles produced by turbulent bubble break-up, we propose a population balance framework in which break-up involves two physical processes: an inertial deformation to the parent bubble that sets the size of large child bubbles, and a capillary instability that sets the size of small child bubbles. A Monte Carlo approach is used to construct the child size distribution, with simulated stochastic break-ups constrained by our experimental measurements and the understanding of the role of capillarity in small bubble production. This approach reproduces the experimental time evolution of the bubble size distribution during the disintegration of large air cavities in turbulence.

The advection–diffusion of a small surface element of scalar in three dimensions (or of a small line element in two dimensions) is solved analytically thanks to the Ranz transform (Ranz, AIChE J., vol. 25, issue 1, 1979, pp. 41–47). As the quantum or elementary brick of any complex mixture, we call this element a diffuselet. Its evolution is computed numerically from the integration of the velocity gradient along the trajectory, as classically done for the Lyapunov exponents. The concentration profile across the diffuselet is obtained from the product of its initial orientation with a dimensionless tensor. Averaging over all initial orientations yields simple formulae for the mean scalar variance and the scalar probability distribution function (p.d.f.). This technique is then applied to two-dimensional and three-dimensional sine flows, in excellent agreement with direct numerical simulations. For these simple flows, the temporal integration is obtained analytically leading to simple integrals for the scalar variance and p.d.f. Statistics of stretching rates are calculated as well. The Lyapunov exponent is close to the value for short-time correlated flows (Kraichnan, J. Fluid Mech., vol. 64, issue 4, 1974, pp. 737–762) in the case of a small displacement during each step; it is close to the value for a simple shear in the case of a large displacement. The p.d.f. of stretching factors are log normal with a ratio between the mean and the variance equal to half the dimension of space for small displacements (in agreement with Kraichnan, J. Fluid Mech., vol. 64, issue 4, 1974, pp. 737–762), but increases strongly for large displacements.

Both one-dimensional in the horizontal direction (1DH, dispersive and non-dispersive) and two-dimensional in the horizontal direction (2DH) axisymmetric (approximate, non-dispersive) analytical solutions are derived for water waves generated by moving atmospheric pressures. For 1DH, three wave components can be identified: the locked wave propagating with the speed of the atmospheric pressure, $C_p$, and two free wave components propagating in opposite directions with the respective wave celerity, according to the linear frequency dispersion relationship. Under the supercritical condition ($C_p > C$, which is the fastest celerity of the water wave), the leading water wave is the locked wave and has the same sign (i.e. phase) as the atmospheric pressure, while the trailing free wave has the opposite sign. Under the subcritical condition ($C >C_p$) the fastest moving free wave component leads, and its free surface elevation has the same sign as the atmospheric pressure. For a long atmospheric pressure disturbance, the induced free surface profile mimics that of the atmospheric pressure. The 2DH problem involves an axisymmetric atmospheric pressure decaying in the radial direction as $O(r^{-1/2})$. Due to symmetry, only two wave components, locked and free, appear. The tsunami DART data captured during Tonga's volcanic eruption event are analysed. Corrections are necessary to isolate the free surface elevation data. Comparisons between the corrected DART data and the analytical solutions, including the arrival times of the leading locked waves and the trailing free waves, and the amplitude ratios, are in agreement in order of magnitude.

Direct numerical simulations of turbulent pipe flow subjected to streamwise-varying wall rotation are performed. This control method is able to achieve drag reduction and even relaminarize the flow under certain control parameters at friction Reynolds number $Re_\tau =180$. Two control parameters, which are velocity amplitude and wavelength, are considered. It is found that increasing the wavelength rather than increasing the amplitude seems to be a better choice to improve the control efficiency. An annular boundary layer, called the spatial Stokes layer (SSL), is formed by the wall rotation. Based on the thickness of the SSL, two types of drag-reduction scenarios can be identified roughly. When the thickness is low, the SSL acts as a spacer layer, inhibiting the formation of streamwise vortices and thereby reducing the shear stress. The flow structures outside the SSL are stretched in the streamwise direction due to the increased velocity gradient. Within the SSL, the turbulence intensity diminishes dramatically. When the thickness is large, a streamwise wavy pattern of near-wall streaks is formed. The streak orientation is dominated by the mean shear-strain vector outside the viscous sublayer, and there is a phase difference between the streak orientation and local mean velocity vector. The streamwise scales of near-wall flow structures are reduced significantly, resulting in the disruption of downstream development of flow structures and hence leading to the drag reduction. Furthermore, it is found that it requires both large enough thickness of the SSL and velocity amplitude to relaminarize the turbulence. The relaminarization mechanism is that the annular SSL can absorb energy continuously from wall-normal stress due to the rotational effect, thereby the turbulence self-sustaining process cannot be maintained. For the relaminarization cases, the laminar state is stable to even extremely large perturbations, which possibly makes the laminar state the only fixed point for the whole system.

Inspired by the recent realization of a two-dimensional (2-D) chiral fluid as an active monolayer droplet moving atop a 3-D Stokesian fluid, we formulate mathematically its free-boundary dynamics. The surface droplet is described as a general 2-D linear, incompressible and isotropic fluid, having a viscous shear stress, an active chiral driving stress and a Hall stress allowed by the lack of time-reversal symmetry. The droplet interacts with itself through its driven internal mechanics and by driving flows in the underlying 3-D Stokes phase. We pose the dynamics as the solution to a singular integral–differential equation, over the droplet surface, using the mapping from surface stress to surface velocity for the 3-D Stokes equations. Specializing to the case of axisymmetric droplets, exact representations for the chiral surface flow are given in terms of solutions to a singular integral equation, solved using both analytical and numerical techniques. For a disc-shaped monolayer, we additionally employ a semi-analytical solution that hinges on an orthogonal basis of Bessel functions and allows for efficient computation of the monolayer velocity field, which ranges from a nearly solid-body rotation to a unidirectional edge current, depending on the subphase depth and the Saffman–Delbrück length. Except in the near-wall limit, these solutions have divergent surface shear stresses at droplet boundaries, a signature of systems with codimension-one domains embedded in a 3-D medium. We further investigate the effect of a Hall viscosity, which couples radial and transverse surface velocity components, on the dynamics of a closing cavity. Hall stresses are seen to drive inward radial motion, even in the absence of edge tension.

The unsteady hydrodynamics of two pitching foils arranged in a side-by-side (parallel) configuration is examined for a range of Strouhal numbers, phase differences, oscillation amplitudes and separation distances. Three distinct vortex patterns are identified in the wake maps, which include separated wake, merged wake and transitional-merged wake. Furthermore, a novel model is introduced based on fundamental flow variables including velocity, location and circulation of dipole structures to quantitatively distinguish vortex patterns in the wake. The physical mechanism of the wake merging process is also elucidated. When an oscillating foil experiences the jet deflection phenomenon, secondary structures separated from the primary street traverse in the other direction by making an angle with its parent vortex street. For in-phase pitching parallel foils, secondary structures from the vortex street of the lower foil interact with the primary vortex street of the upper foil under certain kinematic conditions. This interaction triggers the wake merging process by influencing circulation of coherent structures in the upper part of the wake. It is unveiled that merging of the wakes leads to enhancements in propulsive efficiency by increasing thrust generation without a significant alteration in power requirements. These are attributed to the formation of a high-momentum jet by the merged vortex street, which possesses significantly larger circulation due to the amalgamation of the vortices, and major alterations in the evolution of leading edge vortices. Thus, flow physics, which is thoroughly explored here, is crucial in providing novel insights for the future development of flow control techniques for efficient designs of bio-inspired underwater propulsors.