Modelling multiscale systems from nanoscale to macroscale requires the use of atomistic and continuum methods and, correspondingly, different computer codes. Here, we develop a seamless method based on DeepONet, which is a composite deep neural network (a branch and a trunk network) for regressing operators. In particular, we consider bubble growth dynamics, and we model tiny bubbles of initial size from 100 nm to 10 $\mathrm {\mu }\textrm {m}$, modelled by the Rayleigh–Plesset equation in the continuum regime above 1 $\mathrm {\mu }\textrm {m}$ and the dissipative particle dynamics method for bubbles below 1 $\mathrm {\mu }\textrm {m}$ in the atomistic regime. After an offline training based on data from both regimes, DeepONet can make accurate predictions of bubble growth on-the-fly (within a fraction of a second) across four orders of magnitude difference in spatial scales and two orders of magnitude in temporal scales. The framework of DeepONet is general and can be used for unifying physical models of different scales in diverse multiscale applications.

By coupling direct numerical simulation of homogeneous isotropic turbulence with a localised solution of the convection–diffusion equation, we model the rate of transfer of a solute (mass transfer) from the surface of small, neutrally buoyant, axisymmetric, ellipsoidal particles (spheroids) in dilute suspension within a turbulent fluid at large Péclet number, $\textit {Pe}$. We observe that, at $\textit {Pe} = O(10)$, the average transfer rate for prolate spheroids is larger than that of spheres with equivalent surface area, whereas oblate spheroids experience a lower average transfer rate. However, as the Péclet number is increased, oblate spheroids can experience an enhancement in mass transfer relative to spheres near an optimal aspect ratio $\lambda \approx 1/4$. Furthermore, we observe that, for spherical particles, the Sherwood number $\textit {Sh}$ scales approximately as $\textit {Pe}^{0.26}$ over $\textit {Pe} = 1.4\times 10^{1}$ to $1.4\times 10^{4}$, which is below the $\textit {Pe}^{1/3}$ scaling observed for inertial particles but consistent with available experimental data for tracer-like particles. The discrepancy is attributed to the diffusion-limited temporal response of the concentration boundary layer to turbulent strain fluctuations. A simple model, the quasi-steady flux model, captures both of these phenomena and shows good quantitative agreement with our numerical simulations.

In this study, large-eddy simulations are utilised to unravel the influence of the nozzle's external geometry on upstream-travelling waves in under-expanded supersonic impinging jets. Three configurations, a thin-lipped, a thin-lipped with a sponge and an infinite-lipped nozzle are considered with the other non-dimensionalised geometrical and flow variables identical for the three cases. Spectral proper orthogonal decomposition is applied to the Mack norm, i.e. the energy norm based on the stagnation energy, to obtain the spatial modes at their corresponding frequency. The spectral decomposition of the spatial modes at optimal and suboptimal frequencies is used to isolate the wavepackets into upstream- and downstream-propagating waves based on their phase velocity. It is found that the external geometry of the nozzle has a significant influence on the first-order statistics even though the governing non-dimensional parameters are the same for all three cases. Multiple peaks emerge in the energy spectra at distinct frequencies corresponding to axisymmetric azimuthal modes for each case. The downstream-propagating wavepackets have a high amplitude at the shear layer of the three jets with the mode shapes resembling Kelvin–Helmholtz instability waves, while the upstream-travelling wavepackets exist in the three regions of the near field, shear layer and inside of the jet. The barrel shock at the nozzle exit appears as a flexible shield, which prevents upstream-travelling waves from reaching the internal region of the nozzle, where the upstream-travelling waves travel obliquely with one side of the wavefront is crawling on the reflected shock while the other side is guided by the shear layer. These latter waves can reach the nozzle lip via inside of the jet. The spectral decomposition of the spatial modes at optimal and suboptimal frequencies show that all three forms of the near field, shear layer and inside jet upstream-travelling wavepackets contribute to the receptivity process while their contributions and strength are altered by the change of the external geometry of the nozzle.

In this work, the fluid dynamics and heat transfer of time-dependent flows with shear-thinning behaviour over two confined square cylinders in tandem arrangement are studied numerically. The case studies include two- and three-dimensional flows under a wide range of power-law indices, $0.25\leq n \leq 1.0$, and blockage ratios, $\beta =0.50$, 0.66 and 0.80, for a fixed Reynolds number of $Re=100$ and Prandtl number of $Pr=10$. The fluid dynamic analysis includes detailed qualitative and quantitative comparisons between the different fluids and blockage ratios, where streamlines, viscosity fields, and lift and drag coefficients are presented. Moreover, a detailed study of the route from laminar time-dependent to chaotic flows is included. It was determined that the flow exhibits a transition from laminar to chaotic by decreasing the power-law index ($n$) and increasing the blockage ratio ($\beta$). With respect to the thermal analysis, isotherms and Nusselt numbers are compared between the different case studies. This analysis demonstrates that the average Nusselt numbers increased in chaotic flows. The three-dimensional cases confirmed the results proposed for the two-dimensional case.

To understand how a spherical geometry influences the dynamics of gravity-driven subduction of the oceanic lithosphere on Earth, we study a simple model of a thin and dense axisymmetric shell of thickness $h$ and viscosity $\eta _1$ sinking in a spherical body of fluid with radius $R_0$ and a lower viscosity $\eta _0$. Using scaling analysis based on thin viscous shell theory, we identify a fundamental length scale, the ‘bending length’ $l_b$, and two key dimensionless parameters that control the dynamics: the ‘flexural stiffness’ $St = (\eta _1/\eta _0)(h/l_b)^3$ and the ‘sphericity number’ $\varSigma = (l_b/R_0)\cot \theta _t$, where $\theta _t$ is the angular radius of the subduction trench. To validate the scaling analysis, we obtain a suite of instantaneous numerical solutions using a boundary-element method based on new analytical point-force Green functions that satisfy free-slip boundary conditions on the sphere's surface. To isolate the effect of sphericity, we calculate the radial sinking speed $V$ and the hoop stress resultant $T_2$ at the leading end of the subducted part of the shell, both normalised by their ‘flat-Earth’ values (i.e. for $\varSigma = 0$). For reasonable terrestrial values of $\eta _1/\eta _0$ ($\approx$ several hundred), sphericity has a modest effect on $V$, which is reduced by $< 7\,\%$ for large plates such as the Pacific plate and by up to 34 % for smaller plates such as the Cocos and Philippine Sea plates. However, sphericity has a much greater effect on $T_2$, increasing it by up to 64 % for large plates and 240 % for small plates. This result has important implications for the growth of longitudinal buckling instabilities in subducting spherical shells.

A quantitative assessment of the acoustic source field produced by a laboratory-scale heated jet with a gas dynamic Mach number of 1.55 and an acoustic Mach number of 2.41 is performed using arrays of microphones that are traversed across the axial and radial plane of the jet's acoustic field. The nozzle contour comprises a method of characteristics shape so that shock-related noise is minimal and the dominant sound production mechanism is from Mach waves. The spatial topography of the overall sound pressure level is shown to be dominated by a distinct lobe residing on the principal acoustic emission path, which is expected from flows of this kind with supersonic convective acoustic Mach numbers. The sound field is then analysed on a per-frequency basis in order to identify the location, strength, convection velocity and propagation angle of the various axially distributed noise sources. The analysis reveals a collection of unique data-informed polar patterns of the sound intensity for each frequency. It is shown how these polar patterns can be propagated to any point in the far field with extreme accuracy using the inverse square law. Doing so allows one to gauge the kinds of errors that are encountered using a nozzle-centred source to calculate sound pressure spectrum levels and acoustic power. It is proposed that the measurement strategy described here be used for situations where measurements are being used to compare different facilities, for extrapolating measurements to different geometric scales, for model validation or for developing noise control strategies.

The impact of a hydrogel sphere onto a granular target results in both the deformation of the sphere and the formation of a prominent topographic feature known as an impact crater on the granular surface. We investigate the crater formation and scaling, together with the spreading diameter and post-impact dynamics of spheres by performing a series of experiments, varying the Young's modulus $Y$ and impact speed $U_{0}$ of the hydrogel spheres, and the packing fraction and grain size of the granular target. We determine how the crater diameter and depth depend on $Y$ and show the data to be consistent with those from earlier experiments using droplets and hard spheres. Most specifically, we find that the crater diameter data are consistent with a power law, where the power exponent changes more sharply when $Y$ becomes less than 200 Pa. Next, we introduce an estimate for the portion of the impact kinetic energy that is stored as elastic energy during impact, and thus correct the energy that remains available for crater formation. Subsequently, we determine the deformation of the hydrogel spheres and find that the normalized spreading diameter data are well collapsed introducing an equivalent velocity from an energy balance of the initial kinetic energy against surface and elastic energy. Finally, we observe that under certain intermediate values for the Young's modulus and impact velocities, the particles rebound from the impact crater. We determine the phase diagram and explain our findings from a comparison of the elastocapillary spreading time and the impact duration.

Long and slender liquid filaments are produced during inkjet printing, which can subsequently either retract to form a single droplet, or break up to form a primary droplet and one or more satellite droplets. These satellite droplets are undesirable since they degrade the quality and reproducibility of the print, and lead to contamination within the enclosure of the print device. Existing strategies for the suppression of satellite droplet formation include, among others, adding viscoelasticity to the ink. In the present work, we aim to improve the understanding of the role of viscoelasticity in suppressing satellite droplets in inkjet printing. We demonstrate that very dilute viscoelastic aqueous solutions (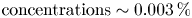$\text {concentrations} \sim 0.003\,\%$ wt. polyethylene oxide, corresponding to nozzle Deborah number 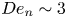$De_{n}\sim 3$) can suppress satellite droplet formation. Furthermore, we show that, for a given driving condition, upper and lower bounds of polymer concentration exist, within which satellite droplets are suppressed. Satellite droplets are formed at concentrations below the lower bound, while jetting ceases for concentrations above the upper bound (for fixed driving conditions). Moreover, we observe that, with concentrations in between the two bounds, the filaments retract at velocities larger than the corresponding Taylor–Culick velocity for the Newtonian case. We show that this enhanced retraction velocity can be attributed to the elastic tension due to polymer stretching, which builds up during the initial jetting phase. These results shed some light on the complex interplay between inertia, capillarity and viscoelasticity for retracting liquid filaments, which is important for the stability and quality of inkjet printing of polymer solutions.

The transition criteria seen from the ground frame are studied in this paper for asymmetrical reflection between shock waves moving at constant linear speed. To limit the size of the parameter space, these criteria are considered in detail for the reduced problem where the upper incident shock wave is moving and the lower one is steady, and a method is provided for extension to the general problem where both the upper and lower ones are unsteady. For the reduced problem, we observe that, in the shock angle plane, shock motion lowers or elevates the von Neumann condition in a global way depending on the direction of shock motion, and this change becomes less important for large shock angle. The effect of shock motion on the detachment condition, though small, displays non-monotonicity. The shock motion changes the transition criteria through altering the effective Mach number and shock angle, and these effects add for small shock angle and mutually cancel for large shock angle, so that shock motion has a less important effect for large shock angle. The role of the effective shock angle is not monotonic on the detachment condition, explaining the observed non-monotonicity for the role of shock motion on the detachment condition. Furthermore, it is found that the detachment condition has a wavefunction form that can be approximated as a hybrid of a sinusoidal function and a linear function of the shock angle.

The multiscale dynamics of a shock–droplet interaction is crucial in understanding the atomisation of droplets due to external airflow. The interaction phenomena are classified into wave dynamics (stage I) and droplet breakup dynamics (stage II). Stage I involves the formation of different wave structures after an incident shock impacts the droplet surface. These waves momentarily change the droplet's ambient conditions, while in later times they are mainly influenced by shock-induced airflow. Stage II involves induced airflow interaction with the droplet that leads to its deformation and breakup. Primarily, two modes of droplet breakup, i.e. shear-induced entrainment and Rayleigh–Taylor piercing (RTP) (based on the modes of surface instabilities) were observed for the studied range of Weber numbers $(We\sim 30\text{--}15\,000)$. A criterion for the transition between two breakup modes is obtained, which successfully explains the observation of RTP mode of droplet breakup at high Weber numbers $(We\sim 800)$. For $We > 1000$, the breakup dynamics is governed by the shear-induced surface waves. After formation, the Kelvin–Helmholtz waves travel on the droplet surface and merge to form a liquid sheet near the droplet equator. Henceforth, the liquid sheet undergoes breakup processes via nucleation of several holes. The breakup process is recurrent until the complete droplet disintegrates or external drag acting on the droplet is insufficient for further disintegration. At lower Weber numbers, the droplet undergoes complete deformation like a flattened disk, and a multibag mode of breakup based on RTP is observed.

The dynamics of suspensions plays a crucial role in the evolution of geophysical systems such as lava lakes, magma chambers and magma oceans. During their cooling and solidification, these magmatic bodies involve convective viscous fluids and dispersed solid crystals that can form either a cumulate or a floating lid by sedimentation. We study such systems based on internal heating convection experiments in high Prandtl fluids bearing plastic beads. We aim to determine the conditions required to produce a floating lid or a sedimented deposit. We show that, although the sign of particles buoyancy is the key parameter, it is not sufficient to predict the particles fate. To complement the model we introduce the Shields formalism and couple it with scaling laws describing convection. We propose a generalized Shields number that enables a self-consistent description of the fate of particles in the system, especially the possibility to segregate from the convective bulk. We provide a quantification of the partition of the mass of particles in the different potential reservoirs (bulk suspension, floating lid, settled cumulate) through reconciling the suspension stability framework with the Shields formalism. We illustrate the geophysical implications of the model by revisiting the problem of the stability of flotation crusts on solidifying rocky bodies.

We present an investigation of the fundamental physical processes involved in deep-water gravity wave breaking. Our motivation is to identify the underlying reason causing the deficiency of the eddy viscosity breaking model (EVBM) in predicting surface elevation for strongly nonlinear waves. Owing to the limitation of experimental methods in the provision of high-resolution flow information, we propose a numerical methodology by developing an EVBM enclosed standalone fully nonlinear quasi-potential (FNP) flow model and a coupled FNP plus Navier–Stokes flow model. The numerical models were firstly verified with a wave train subject to modulational instability, then used to simulate a series of broad-banded focusing wave trains under non-, moderate- and strong-breaking conditions. A systematic analysis was carried out to investigate the discrepancies of numerical solutions produced by the two models in surface elevation and other important physical properties. It is found that EVBM predicts accurately the energy dissipated by breaking and the amplitude spectrum of free waves in terms of magnitude, but fails to capture accurately breaking induced phase shifting. The shift of phase grows with breaking intensity and is especially strong for high-wavenumber components. This is identified as a cause of the upshift of the wave dispersion relation, which increases the frequencies of large-wavenumber components. Such a variation drives large-wavenumber components to propagate at nearly the same speed, which is significantly higher than the linear dispersion levels. This suppresses the instant dispersive spreading of harmonics after the focal point, prolonging the lifespan of focused waves and expanding their propagation space.

A computational study is presented on cross-stream migration and focusing of deformable capsules in curved microchannels of square and rectangular sections under inertial and non-inertial regimes. The numerical methodology is based on immersed boundary methods for fluid–structure coupling, a finite-volume-based flow solver and finite-element method for capsule deformation. Different focusing behaviours in the two regimes are predicted that arise due to the interplay of inertia, deformation, altered shear gradient, streamline curvature effect and secondary flow. In the non-inertial regime, a single-point focusing occurs on the central plane, and at a radial location between the interior face (i.e. face with highest curvature) of the channel and the location of zero shear. The focusing position is nearly independent of capsule deformability (represented by the capillary number, $Ca$). A two-step migration is observed that is comprised of a faster radial migration, followed by a slower migration toward the centre plane. The focusing location progressively moves further toward the interior face with increasing curvature and width, but decreasing height. In the inertial regime, single-point focusing is observed near the interior face for channel Reynolds number $Re_{C}\sim {O}(1)$, that is also highly sensitive to $Re_{C}$ and $Ca$, and moves progressively toward the exterior face with increasing $Re_{C}$ but decreasing $Ca$. As $Re_{C}$ increases by an order, secondary flow becomes stronger, and two focusing locations appear close to the centres of the Dean vortices. This location becomes practically independent of $Ca$ at even higher inertia. The inertial focusing positions move progressively toward the exterior face with increasing channel width and decreasing height. For wider channels, the equilibrium location is further toward the exterior face than the vortex centre.

The initial flow past an impulsively started translating circular cylinder is asymptotically analysed using a Brinkman penalization method on the Navier–Stokes equations. The asymptotic solution obtained shows that the tangential and normal slip velocities on the cylinder surface are of the order of $1/\sqrt {\lambda }$ and $1/\lambda$, respectively, within the second approximation of the present asymptotic analysis, where $\lambda$ is the penalization parameter. This result agrees with the estimation of Carbou & Fabrie (Adv. Diff. Equ., vol. 8, 2003, pp. 1453–1480). Based on the asymptotic solution, the influence of the penalization parameter $\lambda$ is discussed on the drag coefficient that is calculated using the adopted three formulae. It can then be found that the drag coefficient calculated from the integration of the penalization term exhibits a half-value of the results of Bar-Lev & Yang (J. Fluid Mech., vol. 72, 1975, pp. 625–647) as $\lambda \to \infty$.

The nonlinear hydrodynamic responses of a novel spar-type soft-moored floating offshore wind turbine are investigated via analysis of motion measurements from a wave-basin campaign. A prototype of the TetraSpar floater, supporting a $1:60$ scale model of the DTU 10 MW reference wind turbine, was subjected to irregular wave forcing (with no wind) and shown to exhibit subharmonic resonant motions, which greatly exceeded the wave-frequency motions. These slow-drift responses are excited nonlinearly, since the rigid-body natural frequencies of the system lie below the incident-wave frequency range. Pitch motion is examined in detail, allowing for identification of different hydrodynamic forcing mechanisms. The resonant response is found to contain odd-harmonic components, in addition to the even harmonics expected a priori and excited by second-order difference-frequency hydrodynamic interactions. Data analysis utilising harmonic separation and signal conditioning suggests that Morison drag excitation or third-order subharmonic potential flow forcing could be at play. In the extreme survival-conditions sea state, the odd resonant responses are identified to be drag-driven. Their importance for the tested floater is appreciable, as their magnitude is comparable to the second-order potential flow effects. Under such severe conditions, the turbine would not be operating, and as such neglecting aerodynamic forcing and motion damping is likely to be reasonable. Additionally, other possible drivers of the resonant pitch response are explored. Both Mathieu-type parametric excitation and wavemaker-driven second-order error waves are found to have negligible influence. However, we note slight contamination of the measurements arising from wave-basin sloshing.

The effect of wall temperature on the transfer of kinetic energy in a hypersonic turbulent boundary layer for different Mach numbers and wall temperature ratios is studied by direct numerical simulation. A cold wall temperature can enhance the compressibility effect in the near-wall region through increasing the temperature gradient and wall heat flux. It is shown that the cold wall temperature enhances the local reverse transfer of kinetic energy from small scales to large scales, and suppresses the local direct transfer of kinetic energy from large scales to small scales. The average filtered spatial convection and average filtered viscous dissipation are dominant in the near-wall region, while the average subgrid-scale flux of kinetic energy achieves its peak value in the buffer layer. It is found that the wall can suppress the inter-scale transfer of kinetic energy, especially for the situation of a cold wall. A strong local reverse transfer of fluctuating kinetic energy is identified in the buffer layer in the inertial range. Helmholtz decomposition is applied to analyse the compressibility effect on the subgrid-scale flux of kinetic energy. A strong transfer of the solenoidal component of fluctuating kinetic energy is identified in the buffer layer, while a significant transfer of the dilatational component of fluctuating kinetic energy is observed in the near-wall region. It is also shown that compression motions have a major contribution to the direct transfer of fluctuating kinetic energy, while expansion motions play a marked role in the reverse transfer of fluctuating kinetic energy.

The effects of porous material on the aeroacoustic sound generated in a two-dimensional low-Reynolds-number flow ($Re=150$) past a circular cylinder are studied by direct numerical simulation in which the acoustic waves of small amplitudes are obtained directly as a solution to the compressible Navier–Stokes equations. Two models are introduced for the porous material: the microscopic model, in which the porous material is a collection of small cylinders, and the macroscopic model, in which the porous material is continuum characterized by permeability. The corrected volume penalization method is used to deal with the core cylinder, the small cylinders and the porous material. In the microscopic model, significant reduction of the aeroacoustic sound is found depending on the parameters; the maximum reduction of $24.4$ dB from the case of a bare cylinder is obtained. The results obtained for the modified macroscopic model are in good agreement with those obtained for the microscopic model converted by the theory of homogenization, which establishes that the microscopic and macroscopic models are consistent and valid. The detailed mechanism of sound reduction is elucidated. The presence of a fluid region between the porous material and the core cylinder is important for sound reduction. When the sound is strongly reduced, the pressure field behind the cylinder becomes nearly uniform with a high value to stabilize the shear layer in the wake; as a result, the vortex shedding behind the cylinder is delayed to the far wake to suppress the unsteady vortex motion near the cylinder, which is responsible for the aeroacoustic sound.

In this work we study the convection flow driven by a heat-releasing concentration field which itself is stably stratified. The heat-releasing rate is linearly proportional to concentration. Linear stability analysis is conducted to determine the critical heat-releasing rate for given fluid properties and concentration differences. The most unstable mode associated with the critical heat-releasing rate can be oscillatory for a large concentration Rayleigh number, i.e. the non-dimensionalized concentration difference and large Schmidt number, i.e. the ratio of viscosity to diffusivity of the concentration component. Fully developed flows are then investigated by direct numerical simulations. Flow structures near the bottom plate have larger horizontal scales than those near the top plate. The concentration in the bulk is almost constant and takes a similar value for all the explored parameters, which results in the convective flux increasing linearly with height. To explain the dependences of the global transport properties, we extend the unifying theory of the Rayleigh–Bénard convection to the current system and develop scaling laws for the global fluxes. The numerical results can be described accurately by the theoretical model.

The primary instability of the flow past rectangular cylinders is studied to comprehensively describe the influence of the aspect ratio $AR$ and of rounding the leading- and/or trailing-edge corners. Aspect ratios ranging between $0.25$ and $30$ are considered. We show that the critical Reynolds number ($\textit {Re}_c$) corresponding to the primary instability increases with the aspect ratio, starting from $\textit {Re}_c \approx 34.8$ for $AR=0.25$ to a value of $\textit {Re}_c \approx 140$ for $AR = 30$. The unstable mode and its dependence on the aspect ratio are described. We find that positioning a small circular cylinder in the flow modifies the instability in a way strongly depending on the aspect ratio. The rounded corners affect the primary instability in a way that depends on both the aspect ratio and the curvature radius. For small $AR$, rounding the leading-edge corners has always a stabilising effect, whereas rounding the trailing-edge corners is destabilising, although for large curvature radii only. For intermediate $AR$, instead, rounding the leading-edge corners has a stabilising effect limited to small curvature radii only, while for $AR \geqslant 5$ it has always a destabilising effect. In contrast, for $AR \geqslant 2$ rounding the trailing-edge corners consistently increases $\textit {Re}_c$. Interestingly, when all the corners are rounded, the flow becomes more stable, at all aspect ratios. An explanation for the stabilising and destabilising effect of the rounded corners is provided.

The main goal of the present study is to thoroughly test the recently derived OBurnett equations for the normal shock wave flow problem for a wide range of Mach number ($3 \leq Ma \leq 9$). A dilute gas system composed of hard-sphere molecules is considered and the numerical results of the OBurnett equations are validated against in-house results from the direct simulation Monte Carlo method. The primary focus is to study the orbital structures in the phase space (velocity–temperature plane) and the variation of hydrodynamic fields across the shock. From the orbital structures, we observe that the heteroclinic trajectory exists for the OBurnett equations for all the Mach numbers considered, unlike the conventional Burnett equations. The thermodynamic consistency of the equations is also established by showing positive entropy generation across the shock. Further, the equations give smooth shock structures at all Mach numbers and significantly improve upon the results of the Navier–Stokes equations. With no tweaking of the equations in any way, the present work makes two important contributions by putting forward an improved theory of shock waves and establishing the validity of the OBurnett equations for solving complex flow problems.