Understanding the transport of micro-organisms in pipes is crucial to many fundamental problems, such as bioconvection and biodiesel production. In this work, we investigate the velocity profile and dispersion of a suspension of negatively buoyant, gyrotactic micro-organisms in a vertical pipe. With an imposed flow rate, the non-uniform radial cell concentration typical of gyrotaxis distorts the simple Poiseuille flow through inhomogeneous buoyancy, which in turn affects the cell concentration distribution. By solving the fundamental Smoluchowski equation and the Navier–Stokes equation simultaneously, we account for this bidirectional buoyancy–flow coupling effect. Asymptotic dispersion coefficients, namely, drift velocity and dispersivity, are further calculated with the obtained radial velocity and cell concentration profiles, which are assumed to be steady, symmetric and axially invariant. Using the gyrotactic micro-organism Chlamydomonas augustae as an example, detailed results are given to illustrate the effect of buoyancy–flow coupling. In downwelling flows, the buoyancy–flow coupling effect intensifies with the Richardson number $Ri$ quantifying the mean cell concentration, but is strongest at a moderate flow strength. The buoyancy–flow coupling effect significantly enhances the velocity and cell concentration in the central region, as well as the drift velocity and dispersivity. In contrast, the buoyancy–flow coupling effect is comparatively limited in upwelling flows, due to the dominant influence of the no-slip boundary condition imposed at the wall. Comparisons with predictions of existing approximate models are also presented.

The hydrodynamics of bubble columns in the heterogeneous regime is investigated from experiments with bubbles at large particle Reynolds numbers and without coalescence. The void fraction field $\varepsilon$ at small scales, analysed with Voronoï tessellations, corresponds to a random Poisson process (RPP) in homogeneous conditions but it significantly differs from an RPP in the heterogeneous regime. The distance to an RPP allows identifying meso-scale structures, namely clusters, void regions and intermediate regions. A series of arguments demonstrate that the bubble motion is driven by the dynamics of these structures. Notably, bubbles in clusters (respectively in intermediate regions) are moving up faster, up to 3.5 (respectively 2) times the terminal velocity, than bubbles in void regions whose absolute velocity equals the mean liquid velocity. In addition, the mean unconditional relative velocity of bubbles is recovered from mean relative velocities conditional to meso-scale structures, weighted by the proportion of bubbles in each structure. Assuming buoyancy–inertia equilibrium for each structure, the relative velocity is related to the characteristic size and concentration of meso-scale structures. By considering the latter quantity's values at large gas superficial velocities, a cartoon of the internal flow structure is proposed. Arguments are proposed to help understanding why the relative velocity scales as $(gD\varepsilon )^{1/2}$ (with $D$ the column's diameter and $g$ gravity's acceleration). The proposed cartoon seems consistent with a fast-track mechanism that, for the moderate Rouse numbers studied, leads to liquid velocity fluctuations proportional to the relative velocity. The potential impact of coalescence on the above analysis is also commented.

In Rayleigh Bénard convection, for a range of Prandtl numbers 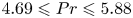$4.69 \leqslant Pr \leqslant 5.88$ and Rayleigh numbers 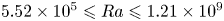$5.52\times 10^5 \leqslant Ra \leqslant 1.21\times 10^9$, we study the effect of shear by the inherent large-scale flow (LSF) on the local boundary layers on the hot plate. The velocity distribution in a horizontal plane within the boundary layers at each 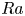$Ra$, at any instant, is (A) unimodal with a peak at approximately the natural convection boundary layer velocities 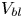$V_{bl}$; (B) bimodal with the first peak between 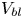$V_{bl}$ and 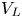$V_{L}$, the shear velocities created by the LSF close to the plate; or (C) unimodal with the peak at approximately 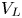$V_{L}$. Type A distributions occur more at lower 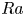$Ra$, while type C occur more at higher 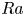$Ra$, with type B occurring more at intermediate 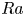$Ra$. We show that the second peak of the bimodal type B distributions, and the peak of the unimodal type C distributions, scale as 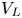$V_{L}$ scales with 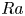$Ra$. We then show that the areas of such regions that have velocities of the order of 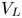$V_{L}$ increase exponentially with increase in 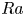$Ra$ and then saturate. The velocities in the remaining regions, which contribute to the first peak of the bimodal type B distributions and the single peak of type A distributions, are also affected by the shear. We show that the Reynolds number based on these velocities scale as 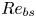$Re_{bs}$, the Reynolds number based on the boundary layer velocities forced externally by the shear due to the LSF, which we obtained as a perturbation solution of the scaling relations derived from integral boundary layer equations. For 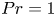$Pr=1$ and aspect ratio 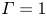$\varGamma =1$, 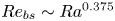$Re_{bs} \sim Ra^{0.375}$ for small shear, similar to the observed flux scaling in a possible ultimate regime. The velocity at the edge of the natural convection boundary layers was found to increase with 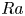$Ra$ as 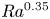$Ra^{0.35}$; since 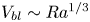$V_{bl}\sim Ra^{1/3}$, this suggests a possible shear domination of the boundary layers at high 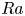$Ra$. The effect of shear, however, decreases with increase in 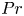$Pr$ and with increase in 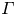$\varGamma$, and becomes negligible for 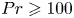$Pr\geqslant 100$ at 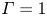$\varGamma =1$ or for 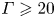$\varGamma \geqslant 20$ at 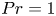$Pr=1$, causing 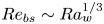$Re_{bs}\sim Ra_w^{1/3}$.

Solute dispersion in Carreau–Yasuda fluid flow in a tube presented in Rana & Murthy (Proc. R. Soc. Lond. A, vol. 472, 2016, p. 20160294) was limited to a steady-state velocity profile due to the nonlinearity associated with the Yasuda parameter $a$ with power-law exponent $n$. This limitation is overcome and the velocity profile is obtained for all values of the Yasuda parameter by using the Lagrange inversion theorem, which admits power series solution for the flow field. An analytical solution for the concentration distribution in the circular tube is obtained for the unsteady and pulsatile flow with $n\leq 1$ and $\alpha <<1$ and the numerical solution is presented for all values of $\alpha$ and $n$. The solute dispersion is analysed analytically using the Sankarasubramanian–Gill generalized dispersion method and also using the Aris–Barton method of moments considering up to fourth-order moments. The solute dispersion is also simulated numerically by using a new class of computationally explicit Runge–Kutta method. The axial mean concentration of the solute is estimated by the exchange, convective and dispersion coefficients. The third- and fourth-order moments give rise to skewness and kurtosis revealing the deviation from the Gaussianity and reduction in the peak of the mean concentration profile at a small time of the solute injection. All time variations of these five moments against flow governing parameters are thoroughly investigated. The flow and dispersion regimes that are derived here for moments provide a good understanding of the solute dispersion in the tube. The increase in the Womersley frequency parameter led to a phase lag at each period. This work is the initiation of estimating the skewness and kurtosis in a non-yield stress fluid flow in a tube.

A comprehensive investigation, using experimental, computational and analytic methods, is reported on the motion of, and the forces on, spheres of different density ratios rolling freely down an incline in a fluid under gravity. The Reynolds number, based on sphere diameter and terminal velocity, ranged up to 1000 for the experiments, and up to 250 for the computer simulations. A modified Reynolds number, incorporating the density ratio, gravitational acceleration and angle of incline, was found to govern the saturated state of the flow. Transition from steady to unsteady flow was sensitive to mass ratio, with lighter spheres undergoing earlier transition. Indeed, positively buoyant spheres develop cross-slope oscillations prior to the onset of shedding. Also of interest, the transition to chaotic wake flow occurs at Reynolds numbers lower than for a sphere forced to roll at a constant speed. In addition to the average sphere motion, flow-induced vibrations were predicted and measured, with quasi-periodic lateral oscillations found to increase as the flow became more unstable, and to decrease with increased density ratio. The study confirms the time-averaged results of a previous experimental study, although closer inspection shows sensitivity to the relative surface roughness of the sphere and plane in experiments; this sensitivity is masked in typical log–log plots of drag against Reynolds number. Physical surface roughness appears to play a role analogous to the necessary imposed gap between the sphere and plane in computations, removing the singularity in drag that would prevent rolling for an incompressible fluid and perfectly smooth surfaces.

This investigation characterises the time response and the transient turbulence dynamics undergone by rapidly decelerating turbulent pipe flows. A series of direct numerical simulations of decelerating flows between two steady Reynolds numbers were conducted for this purpose. The statistical analyses reveal that rapidly decelerating turbulent flows undergo four coherent, unambiguous transitional stages: inertial (stage I), a dramatic change of sign in the viscous force associated with the decay of the viscous shear stress at the wall together with a mild turbulence decay in the viscous sublayer; friction recovery (stage II), a recovery in viscous force and progressive decay in the turbulent inertia at the near-wall region; turbulence decay (stage III), a balanced decay in both turbulent inertia and viscous force at the near-wall and overlap regions; core relaxation (stage IV), slow turbulence decay at the core region. The FIK identity derived by Fukagata, Iwamoto and Kasagi (Phys. Fluids, vol. 14, 2002, L73–L76) was used to understand further how the flow dynamics influence the time response of the skin friction coefficient ($C_f$). The results show that although $C_f$ plateaus during the fourth stage, the turbulent contribution keeps decaying, undershoots and finally recovers to attain its final steady value. The time evolution of the azimuthal vorticity ($\omega _\theta$) flux reveals that as the flow is decelerated, a layer of negative $\omega _\theta$ is produced at the wall during the flow excursion. As time progresses, this negative vorticity propagates in the wall-normal direction, attenuating the pre-existing vorticity and producing a decay in the turbulence levels.

Flow past a rotating step cylinder is investigated through three-dimensional numerical simulations for a diameter ratio of 0.5 and a Reynolds number of 150. The step cylinder comprises two cylinders with different diameters arranged coaxially with a step between them. The rotation rate α is defined as the ratio of the rotation speed of the larger cylinder surface to the free-stream velocity. Vortex shedding happens for both cylinders at α = 0, 0.5 and 1, and is suppressed only for the larger cylinder at α = 2 and 3 and fully suppressed for both cylinders at α = 4. The vortex shedding suppression for the larger cylinder or for both cylinders has significant effects on the wake. The S-, N- and L-cells at α = 0 are in good agreement with those reported in previous studies and still exist at α = 1. The N-cell disappears at α = 0.5, and as a result, the L- and S-cells interact with each other directly at the step position. An additional cellular zone is found at α = 0.5 and 1 and this zone has multiple cells with vortex dislocation between them. At α = 2 and 3, there is a strong hub vortex in the streamwise direction behind the step and the vortices in the wake of the smaller cylinder form helical vortices after they roll around this hub vortex. The hub vortex is generated by the difference between the Magnus effect between the smaller and larger cylinders. At α = 4, the hub vortex still exists but the helical vortices disappear because vortex shedding is suppressed for both cylinders. At this rotation rate, the pressure on the cylinder surface oscillates with a frequency much higher than the vortex shedding frequency. The oscillation of the pressure is caused by the combination of periodic generation of ring vortices and their motion along the span of the larger cylinder.

Gravity–capillary waves are waves influenced by both the effects of surface tension and gravity; these waves are at small scales with wavelength range from approximately 10 cm to less than 1 cm. Gravity–capillary waves play a significant role in air–sea interactions, and they exhibit much different features compared with gravity waves. They can be observed widely on the sea surface. Parasitic waves (capillary waves generated by and that ride on gravity and/or gravity–capillary waves) and micro-breaking can be observed on the water surface with winds; however, the presence of wind makes it difficult to analyse the mechanisms of the wave itself. In this paper, parasitic waves and micro-breaking on gravity–capillary waves are examined experimentally, both in the absence of wind. Parasitic waves and axisymmetric micro-breaking waves are generated mechanically in a convergent channel, where energy density increases due to spatial convergence. Three experimental techniques are used to measure wave properties: planar laser-induced fluorescence, particle image velocimetry and shadowgraphs. The wave profile evolution and vortices beneath the parasitic waves are studied. The micro-breaking of gravity–capillary waves is observed on a surface with added surfactant. The surfactant increases the Bond number, and makes breaking possible in these small-scale waves. Energy dissipation of parasitic waves and micro-breaking is quantified, and the enhanced dissipation caused by parasitic waves is identified through the experiments. In this study, mechanically generated breaking waves with wavelengths less than 10 cm are studied for the first time, without the effect of wind. The results yield insight into wave characteristics and energy dissipation on the air–sea interface at small scales.