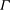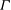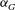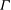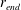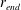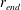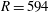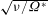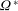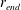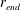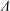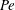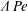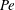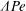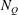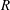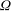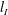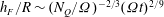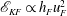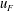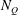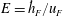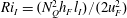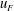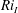We present experimental measurements conducted on freely propagating, turbulent, steady thermal air plumes. Three plumes are studied with differing source conditions, ranging from jet-like, momentum flux dominated releases, to pure plume releases, characterised by a balance between the momentum, volume and buoyancy fluxes at the source. Velocity measurements from near the source to a height of tens of source diameters were made using particle image velocimetry (PIV), providing a high spatial resolution. Temperatures were measured with thermocouples. From these measurements, we investigate the vertical development of the plume fluxes and radial profiles of the mean velocity and temperature. These allow us to analyse the local self-preserving characteristics of the mean flow and to estimate the dependence with height of the plume Richardson number ${\it\Gamma}$. In addition, we analyse the similarity of one-point and two-point second-order velocity statistics, and we discuss the role of ${\it\Gamma}$ on the vertical development of the bulk dynamical parameters of the plume, namely, the turbulent viscosity, the turbulent Prandtl number and the entrainment coefficient ${\it\alpha}_{G}$. Comparison with previous experimental results and with estimates of the entrainment coefficient based on the mean kinetic energy budget allow us to conclude on the influence of ${\it\Gamma}$ on the entrainment process and to explain possible physical reasons for the high scatter in estimates of ${\it\alpha}_{G}$ in the literature.

Numerical simulations of the flow developing on the surface of a rotating disk are presented based on the linearized incompressible Navier–Stokes equations. The boundary-layer flow is perturbed by an impulsive disturbance within a linear global framework, and the effect of downstream turbulence is modelled by a damping region further downstream. In addition to the outward-travelling modes, inward-travelling disturbances excited at the radial end of the simulated linear region, $r_{end}$, by the modelled turbulence are included within the simulations, potentially allowing absolute instability to develop. During early times the flow shows traditional convective behaviour, with the total energy slowly decaying in time. However, after the disturbances have reached $r_{end}$, the energy evolution reaches a turning point and, if the location of $r_{end}$ is at a Reynolds number larger than approximately $R=594$ (radius non-dimensionalized by $\sqrt{{\it\nu}/{\rm\Omega}^{\ast }}$, where ${\it\nu}$ is the kinematic viscosity and ${\rm\Omega}^{\ast }$ is the rotation rate of the disk), there will be global temporal growth. The global frequency and mode shape are clearly imposed by the conditions at $r_{end}$. Our results suggest that the linearized Ginzburg–Landau model by Healey (J. Fluid Mech., vol. 663, 2010, pp. 148–159) captures the (linear) physics of the developing rotating-disk flow, showing that there is linear global instability provided the Reynolds number of $r_{end}$ is sufficiently larger than the critical Reynolds number for the onset of absolute instability.

We model bidisperse size segregation of granular material in quasi-two-dimensional circular tumbler flow using the advection–diffusion transport equation with an additional term to account for segregation due to percolation. Segregation depends on three dimensionless parameters: the ratio of segregation to advection, ${\it\Lambda}$; the ratio of advection to diffusion, $\mathit{Pe}$; and the dimensionless flowing layer depth, ${\it\epsilon}$. The degree of segregation in steady state depends only on the ratio of segregation effects to diffusion effects, ${\it\Lambda}\,\mathit{Pe}$, and the degree of segregation increases as ${\it\Lambda}\mathit{Pe}$ increases. The transient time to reach steady-state segregation depends only on advection, which is manifested in ${\it\epsilon}$ and $\mathit{Pe}$ when ${\it\Lambda}\mathit{Pe}$ is constant. This model is also applied to unsteady tumbler flow, where the rotation speed varies with time.

We consider experimentally an initially quiescent and linearly stratified fluid with buoyancy frequency 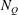$N_{Q}$ in a cylinder subject to surface-stress forcing from a disc of radius 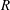$R$ spinning at a constant angular velocity 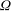${\rm\Omega}$. We observe the growth of the disc-adjacent turbulent mixed layer bounded by a sharp primary interface with a constant characteristic thickness 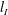$l_{I}$. To a good approximation the depth of the forced mixed layer scales as 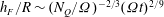$h_{F}/R\sim (N_{Q}/{\rm\Omega})^{-2/3}({\rm\Omega}t)^{2/9}$. Generalising the previous arguments and observations of Shravat et al. (J. Fluid Mech., vol. 691, 2012, pp. 498–517), we show that such a deepening rate is consistent with three central assumptions that allow us to develop a phenomenological energy balance model for the entrainment dynamics. First, the total kinetic energy of the deepening mixed layer 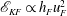$\mathscr{E}_{KF}\propto h_{F}u_{F}^{2}$, where 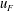$u_{F}$ is a characteristic velocity scale of the turbulent motions within the forced layer, is essentially independent of time and the buoyancy frequency 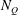$N_{Q}$. Second, the scaled entrainment parameter 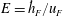$E={\dot{h}}_{F}/u_{F}$ depends only on the local interfacial Richardson number 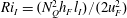$Ri_{I}=(N_{Q}^{2}h_{F}l_{I})/(2u_{F}^{2})$. Third, the potential energy increase (due to entrainment, mixing and homogenisation throughout the deepening mixed layer) is driven by the local energy input at the interface, and hence is proportional to the third power of the characteristic velocity 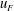$u_{F}$. We establish that internal consistency between these assumptions implies that the rate of increase of the potential energy (and hence the local mass flux across the primary interface) decreases with 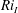$Ri_{I}$. This observation suggests, as originally argued by Phillips (Deep-Sea Res., vol. 19, 1972, pp. 79–81), that the mixing in the vicinity of the primary interface leads to the spontaneous appearance of secondary partially mixed layers, and we observe experimentally such secondary layers below the primary interface.

For the problem describing steady gravity waves with vorticity on a two-dimensional unidirectional flow of finite depth the following results are obtained. (i) Bounds are found for the free-surface profile and for Bernoulli’s constant. (ii) If only one parallel shear flow exists for a given value of Bernoulli’s constant, then there are no wave solutions provided the vorticity distribution is subject to a certain condition.

We examine experimentally the influence of flexibility on the side-to-side fluttering motion of passive wings settling under the influence of gravity. Our results demonstrate the existence of an optimal flexibility that allows flexible wings to remain airborne twice as long as their rigid counterparts of identical mass and size. Flow visualization and measurements allow us to elucidate the role of flexibility in generating increased lift and wing circulation by shedding additional vorticity at the turning point. Theoretical scalings are derived from a reduced model of the flight dynamics and yield quantitative agreement with experiments. These scalings rationalize the strong positive correlation between flexibility and flight time. Our experimental results and theoretical scalings represent an ideal system for the validation of computational approaches to model biologically inspired fluid–structure interaction problems.

While fluid flows are known to promote dissolution of materials, such processes are poorly understood due to the coupled dynamics of the flow and the receding surface. We study this moving boundary problem through experiments in which hard candy bodies dissolve in laminar high-speed water flows. We find that different initial geometries are sculpted into a similar terminal form before ultimately vanishing, suggesting convergence to a stable shape–flow state. A model linking the flow and solute concentration shows how uniform boundary-layer thickness leads to uniform dissolution, allowing us to obtain an analytical expression for the terminal geometry. Newly derived scaling laws predict that the dissolution rate increases with the square root of the flow speed and that the body volume vanishes quadratically in time, both of which are confirmed by experimental measurements.

Flowing over erodible beds, channelized granular avalanches can alter their volume by entraining or detraining basal grains. In detail, entrainment results from a gradual adjustment of stress and velocity profiles over depth, bringing bed material past yield (and vice versa for detrainment). To capture this process, we propose new depth-integrated equations that balance kinetic energy in addition to mass and momentum. The equations require a local granular rheology, assumed viscoplastic, but no extra erosion law. Entrainment rates are instead deduced from the depth-integrated layer dynamics. To check the approach, we obtain solutions for non-equilibrium heap flows, and compare them with experiments conducted in a seesaw channel.