Well-resolved direct numerical simulations of turbulent open channel flows (OCFs) are performed for friction Reynolds numbers up to $Re_\tau =2000$. Various turbulent statistics are documented and compared with the closed channel flows (CCFs). As expected, the mean velocity profiles of the OCFs match well with the CCFs in the near-wall region but diverge notably in the outer region. Interestingly, a logarithmic layer with Kárman constant $\kappa =0.363$ occurs for OCF at $Re_\tau =2000$, distinctly different from CCF. Except for a very thin layer near the free surface, most of the velocity and vorticity variances match between OCFs and CCFs. The one-dimensional energy spectra reveal that the very-large-scale motions (VLSMs) with streamwise wavelength $\lambda _x>3 h$ or spanwise wavelength $\lambda _z>0.5 h$ contribute the most to turbulence intensity and Reynolds shear stress in the overlap and outer layers (where h is the water depth). Furthermore, the VLSMs in OCFs are stronger than those in CCFs, resulting in a slightly higher streamwise velocity variance in the former. Due to the footprint effect, these structures also have significant contributions to the mean wall shear stress, and the difference between OCF and CCF enlarges with increasing $Re_\tau$. In summary, the free surface in OCFs plays an essential role in various flow phenomena, including the formation of stronger VLSMs and turbulent kinetic energy redistribution.

The flat plate transitional boundary layer response to the acceleration induced by the shock wave propagation is studied using large-eddy simulations. The steady boundary layer global behaviour is first investigated before focusing on the transient response of a turbulent region following the shock wave propagation. It is shown that the transient response of the turbulent region exhibits strong similarities with the spatial transition process to turbulence induced by free-stream turbulence, the so-called bypass transition. The boundary layer does not evolve gradually from the initial turbulence intensity to the final turbulence intensity but undergoes a temporal transition process composed of three distinct phases. These three different phases are comparable with the three stages of a bypass transition (i.e. buffeted laminar flow, transition and fully turbulent) because they are governed by the same physical processes. On the other hand, it is highlighted that this temporal response is identical to that described by He & Seddighi (J. Fluid Mech., vol. 715, 2013, pp. 60–102) during the study of an incompressible boundary layer undergoing an increase of mass flow rate. The boundary layer compression by the shock propagation does not contribute to any significant change in the turbulence dynamic after an unsteady acceleration.

High-resolution, long-time three-dimensional simulations are presented for slow, pressure-driven flow of a periodic emulsion of deformable drops through a dense, simple cubic array of solid spheres (one drop and one particle per periodic cell). The drops, covered with insoluble, non-diffusive surfactant, are large compared with pores, and they squeeze with high resistance, very closely coating the solids to overcome surface tension and lubrication effects. The solid volume fraction is 50 %, the emulsion concentration 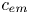$c_{em}$ in the pore space is 36 % or 50 %, the drop-to-medium viscosity ratio 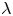$\lambda$ is 0.25 to 4. The contamination measure 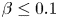$\beta \leq 0.1$ keeps the linear surfactant model (assumed in most of the work) physically relevant. The boundary-integral solution requires extreme resolutions (tens of thousands of boundary elements per surface) achieved by multipole acceleration with special desingularizations, combined with flow-biased surfactant transport algorithms for numerical stability. The time-periodic regime is typically attained after a few squeezing cycles; the motion period is used in the extrapolation scheme to evaluate critical capillary numbers $Ca_{crit}$ demarcating squeezing from trapping. Due to Marangoni stresses, even light (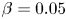$\beta =0.05$) to moderate (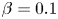$\beta =0.1$) contaminations significantly reduce the average drop-phase migration velocity (up to 2.8 times, compared with clean drops), especially at small 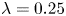$\lambda =0.25$. In contrast, 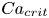$Ca_{crit}$ is weakly sensitive to contamination and levels off completely at 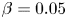$\beta =0.05$. At 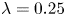$\lambda =0.25$ and 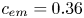$c_{em}=0.36$, the average drop-phase velocities are much different for lightly and moderately contaminated emulsions, except for near-critical squeezing when they become the same. Nonlinear surfactant models (Langmuir, Frumkin) are used to validate the linear model.

This article presents our exploration into how a finite-width internal gravity wave beam is modified by triadic resonance instability. We present both experimental and weakly nonlinear modelling to examine this instability mechanism, in which a primary wave beam generates two secondary wave beams of lower frequencies and shorter length scales. Through a versatile experimental set-up, we examine how this instability evolves over hundreds of buoyancy periods. Unlike predictions from previous zero-dimensional weakly nonlinear theory, we find that the wave does not monotonically approach a saturated equilibrium of triadic interactions; rather, the amplitudes and structures of the constituent beams continue to modulate without ever reaching a steady equilibrium. To understand this behaviour, we develop a weakly nonlinear approach to account for the spatiotemporal evolution of the amplitudes and structures of the beams over slow time scales and long distances, and explore the consequences using a numerical scheme to solve the resulting equations. Through this approach, we establish that the evolution of the instability is remarkably sensitive to the spatiotemporal triadic configuration for the system and how part of the observed modulations can be attributed to a competition between the linear growth rate of the secondary wave beams and the finite residence time of the triadic perturbations within the underlying primary beam.

A ubiquitous arrangement in nature is a free-flowing fluid coupled to a porous medium, for example a river or lake lying above a porous bed. Depending on the environmental conditions, thermal convection can occur and may be confined to the clear fluid region, forming shallow convection cells, or it can penetrate into the porous medium, forming deep cells. Here, we combine three complementary approaches – linear stability analysis, fully nonlinear numerical simulations and a coarse-grained model – to determine the circumstances that lead to each configuration. The coarse-grained model yields an explicit formula for the transition between deep and shallow convection in the physically relevant limit of small Darcy number. Near the onset of convection, all three of the approaches agree, validating the predictive capability of the explicit formula. The numerical simulations extend these results into the strongly nonlinear regime, revealing novel hybrid configurations in which the flow exhibits a dynamic shift from shallow to deep convection. This hybrid shallow-to-deep convection begins with small, random initial data, progresses through a metastable shallow state and arrives at the preferred steady state of deep convection. We construct a phase diagram that incorporates information from all three approaches and depicts the regions in parameter space that give rise to each convective state.

Direct numerical simulations are performed to investigate the wake transitions of the flow normal to a circular rotating disk. The diameter-thickness aspect ratio of the disk is $\chi =50$. The Reynolds number of the free stream is defined as $Re_s=U_\infty D/\nu$, with incoming flow velocity $U_\infty$, disk diameter $D$, and kinematic viscosity of the fluid $\nu$. The rotational motion of the disk is described by the Reynolds number of rotation $Re_r=\varOmega Re_s$, with non-dimensional rotation rate $\varOmega =\frac {1}{2}\omega D/U_\infty$, where $\omega$ is the angular rotation speed of the disk. Extensive numerical simulations are performed in the parameter space $50 \leqslant Re_s \leqslant 250$ and $0 \leqslant Re_r \leqslant 250$, in which six flow regimes are identified as follows: the axisymmetric state, the low-speed steady rotation (LSR) state, the high-speed steady rotation (HSR) state, the low-speed unsteady rotation (LUR) state, the rotational vortex shedding state, and the chaotic state. Although plane symmetry exists in the wake when the disk is stationary, a small rotation will immediately destroy its symmetry. However, the vortex shedding frequencies and wake patterns of the stationary disk are inherited by the unsteady rotating cases at low $Re_r$. A flow rotation rate jump is observed at $Re_s\approx 125$. The LUR state is intermediate between the LSR and HSR states. Due to the rotational motion, the wake of the disk enters the steady rotation state earlier at large $Re_r$, and is delayed into the vortex shedding state in the whole range of $Re_r$. In the steady rotation states (LSR and HSR), the steady flow rotation rate is linearly correlated with the disk rotation rate. It is found that the rotation of the disk can restrain the vortex shedding. The chaotic state can be regularized by the medium rotation speed of the disk.

Motivated by drag-based propulsion of crinoids, the shape reconfiguration of a feather-like elastic structure under both steady and unsteady translational motions is investigated. The simplified elastic structure consists of a centre rod to which numerous side flaps are attached by elastic hinges. These side flaps fold in only one direction to realize a dramatic reduction in the area of the structure during the recovery stroke. Compared with experimental measurements, analytical methods developed to couple the dynamics of the centre rod and the side flaps successfully predict the drag force and three-dimensional reconfiguration of the elastic structure during both power and recovery strokes. A dimensionless speed given by the ratio of inertial fluid force to elastic bending force is proposed for the coupled deflections of the centre rod and side flaps, and is found to determine primarily the reconfiguration of the elastic structure. A reconfiguration number defined specifically for our model provides an appropriate characterization of the effect of side-flap folding on drag force reduction. Moreover, the ratio of drag forces between the power and recovery strokes is evaluated to find model conditions for the optimal force ratio.

We examine the asymmetric flows of aqueous surfactant films over an air bubble. A thin film is formed by raising an equilibrated air bubble through an aqueous solution of Triton X-100 (0.01 mM, below critical micelle concentration). Due to the advection generated by the squeezing motion, the initially uniformly distributed surfactants redistribute and, thus, generate an axisymmetric surface tension gradient that drives a Marangoni flow. The external forcing of raising the bubble also creates an axisymmetric dimpled film with a radial thickness variation that reaches its minimum at the rim of the dimple. The curvature in the film thickness generates an axisymmetric capillary pressure driven flow. When the apex of the bubble has penetrated the initially flat air-solution interface, the rising bubble is stopped and the resulting flow demonstrates symmetry breaking both in the experiment and in the parameter matched numerical simulation. Linear stability analysis reveals the mechanism behind the disturbance growth. It is found that the most dangerous azimuthal wavenumber scales linearly with the ratio of the rim radius to the radial width of significant radial pressure and surface tension gradients after stopping the bubble. Finally, we compare this instability to the previously studied surfactant spreading induced fingering phenomenon (Warner, Craster & Matar, Phys. Fluids, vol. 16, issue 8, 2004, pp. 2933–2951).

We study the interaction between a laser-induced cavitation bubble and a submillimetre-sized water droplet submerged in silicone oil. High-speed imaging reveals the pathways through which droplet fragmentation occurs and three distinct regimes of bubble–droplet interaction are identified: deformation, external emulsification and internal emulsification. We have observed that during the bubble collapse, the droplet elongates towards the bubble, which acts as a flow sink pulling on the droplet. For silicone oils with higher viscosity, the droplet jets into the cavitation bubble and forms a satellite water droplet in the continuous oil phase. In contrast, for lower-viscosity oils, the droplet encapsulates the collapsing bubble as it jets inside and undergoes multiple cycles of expansion and collapse. These internal bubble collapses create tiny oil droplets inside the parent water droplet. The kinematic viscosity of the silicone oil, maximum bubble diameter and centre-to-centre distance between the bubble and the droplet are varied. The regimes are separated in a parameter space set up by the non-dimensional distance and a cavitation Reynolds number.

We take advantage of the extremely small kinematic viscosity of superfluid $^4$He to investigate the propagation of macroscopic vortex rings at Reynolds numbers between $2 \times 10^4$ and $4 \times 10^6$. These inhomogeneous flow structures are thermally generated by releasing short power pulses into a small volume of liquid, open to the surrounding bath through a vertical tube $2$ mm in diameter. We study specifically the ring behaviour between $1.30$ and $1.80$ K using the flow visualization and second sound attenuation techniques. From the obtained data sets, containing more than $2600$ realizations, we find that the rings remain well-defined in space and time for distances up to at least $40$ tube diameters, and that their circulation depends significantly on the travelled distance, in a way similar to that observed for turbulent vortex rings propagating in Newtonian fluids. Additionally, the ring velocity and circulation appear to be influenced solely by a single, experimentally accessible parameter, combining the liquid temperature with the magnitude and duration of the power pulse. Overall, our results support the view that macroscopic vortex rings moving in superfluid $^4$He closely resemble their Newtonian analogues, at least in the absence of significant thermal effects and at sufficiently large flow scales.

The presence of a no-slip, impermeable, adiabatic, sloped boundary in an otherwise quiescent, stably stratified, Boussinesq flow generates baroclinic vorticity within a diffusive boundary layer. Such conditions are typical of the oscillating boundary layers on adiabatic abyssal slopes, sloped lake bathymetry and sloped coastal bathymetry in the absence of high-wavenumber internal waves, mean flows, far-field turbulence on larger scales, and resonant tidal–bathymetric interaction. We investigate the linear stability of the oscillating flow within non-dimensional parameter space typical of the $M_2$ tide and hydraulically smooth, middle-latitude abyssal slopes through Floquet linear stability analysis. The flow dynamics depends on three non-dimensional variables: the Reynolds number for Stokes’ second problem, the Prandtl number, and a frequency ratio that accounts for the resonance conditions ($C$, criticality) of the buoyant restoring force and the tidal forcing. The Floquet analysis results suggest that oscillating laminar boundary layers on adiabatic abyssal slopes are increasingly unstable as Reynolds number, criticality parameter and/or spanwise disturbance wavenumber are increased. We also show that the two-dimensional Floquet linear instability necessarily generates three-dimensional baroclinic vorticity, which suggests that the evolution of the gravitational instabilities may be nonlinear as $t\rightarrow \infty$.

Boundary layer instabilities and shock–boundary-layer interactions (SBLIs) critically affect the performance and safe operation of mixed-compression air intakes. We present a computational study anchored in companion experiments, to evaluate the multimodal mechanisms driving the dynamics of the external compression ramp flow and the cowl SBLI in a Mach $3$ intake. Boundary layer transition over the external ramp is first analysed through a global linear analysis, and the linear estimates are further validated through direct numerical simulations. The separation bubble over the ramp harbours three-dimensional stationary instabilities that induce transition, under the influence of secondary instabilities driven by the shear layer modes of the bubble. The interaction of the resulting turbulized boundary layer with the cowl shock at the ramp–isolator junction and its control through geometrical modification constitutes the second part of the study. We tested a faceted (baseline) and a notched (modified) junction design to evaluate its impact on the low-, mid- and high-frequency scales generated at the cowl SBLI region. In relation to the baseline case, the notched geometry effectively locks the separation point of the bubble, thus attenuating the upstream low-frequency breathing motion. The notch also energizes the midfrequency content through vortex shedding in a well-developed shear layer, which persists into the isolator, thus assisting in an efficient compression process through cross-stream mixing of near-wall flow. The isolator boundary layer in the notched design exhibits relatively lower static pressures and higher velocity fluctuations, which are conducive to improving the flow stability, unstart margin and efficiency of high-speed propulsion systems.

In this study, we demonstrate an efficient approach to investigating the interaction of vortex pairs on a turbulent boundary layer. Our aim is to assess how vortex characteristics impact the downstream flow. Wall-modelled large eddy simulations are used together with an inlet defined by a Batchelor vortex model superimposed on a turbulent boundary layer profile, generated using synthetic turbulence and a precursor Reynolds-averaged Navier–Stokes calculation. This set-up allows for the efficient testing of multiple configurations whilst providing adequate resolution of outer boundary layer and the vortex–vortex interactions. After validating the methodology, we report a set of simulations for both co- and counter-rotating vortex pairs at different separations and asymmetric strengths. The separation distance between the vortices was found to have a significant effect upon the merging of the vortices. Asymmetric strength vortex pairs, analogous to vortex generators in yaw, demonstrate performance independent of flow direction for small angles. Detailed analysis of this flow provides insight into turbulence generation mechanisms and Reynolds stress anisotropy – valuable reference data for the development of lower-order models. Skin-friction enhancement is shown to be more effective for counter-rotating vortex pairs than co-rotating pairs of the same strength and spacing. Additionally, a wider spacing between the initial vortex positions results in a faster rise in the skin-friction coefficient.

We develop a model and numerical method to study the large-amplitude flutter of rectangular membranes (of zero bending rigidity) that shed a trailing vortex-sheet wake in a three-dimensional (3-D) inviscid fluid flow. We apply small initial perturbations and track their decay or growth to large-amplitude steady-state motions. For 12 combinations of boundary conditions at the membrane edges we compute the stability thresholds and the subsequent large-amplitude dynamics across the three-parameter space of membrane mass density, pretension and stretching rigidity. With free side edges we find good agreement with previous 2-D results that used different discretization methods. We find that the 3-D dynamics in the 12 cases naturally forms four groups based on the conditions at the leading and trailing edges. The deflection amplitudes and oscillation frequencies have scalings similar to those in the 2-D case. The conditions at the side edges, although generally less important, may have small or large qualitative effects on the membrane dynamics – e.g. steady vs unsteady, periodic vs chaotic or the variety of spanwise curvature distributions – depending on the group and the physical parameter values.

Linear stabilities of the liquid metal mixed convection in a horizontal pipe under bottom heating and transverse magnetic field are studied through linear global stability analyses. Three branches of the linear stability boundary curves are determined by the eigenvalue computation of the most unstable modes. One branch is located in the region of large Hartmann number and determined by the linear unstable mode which was first revealed by the numerical simulations of Zikanov, Listratov & Sviridov (J. Fluid Mech., vol. 720, 2013, pp. 486–516). This branch curve shows that the global unstable mode exists above a threshold of Hartmann number, which agrees with the experiment of Genin et al. (Temperature fluctuations in a heated horizontal tube affected by transverse magnetic field. In Proc. 8th PAMIR Conf. Fund. Appl. MHD, Borgo, Corsica, France, pp. 37–41, 2011). The other two branch curves determined by two different long-wave unstable modes intersect with each other in the region of small Hartmann number. The critical Grashof number on these two curves increases exponentially with the increase of the Hartmann number. Through energy budget analyses at the critical thresholds of these unstable modes, it is found that, for the unstable mode at large Hartmann numbers, buoyancy is the dominant destabilizing term which demonstrates the hypothetical explanation of Zikanov et al. (2013) who regard natural convection as a destabilization mechanism. It is further revealed that, with respect to the unstable modes on the critical stability curves of small Hartmann numbers, the dominant destabilization comes from the streamwise shear of the basic flow. Finally, within the linear unstable region, fully developed nonlinear flow states of the mixed convection are investigated by direct numerical simulations (DNS) with several sets of selected dimensionless parameters. The spatio-temporal structures of these nonlinear flow states are discussed in detail with comparison with the linear unstable global modes.

The O-type transition caused by a pair of small-amplitude oblique waves in a vertical buoyancy layer of a fluid with Prandtl number $0.71$ at a Reynolds number of $200$ is investigated using linear stability analysis and three-dimensional direct numerical simulation. The small-amplitude oblique waves experience linear growth and undergo nonlinear interactions to generate streamwise vortices/streaks, two-dimensional streamwise waves and harmonic oblique waves. The streamwise vortices/streaks and two-dimensional streamwise waves have twice the spanwise or streamwise wavenumber of the original perturbation, respectively. Unlike the O-type transition in isothermal flat-plate incompressible and compressible boundary layers where streaks dominate the transition, in the vertical buoyancy layer, either streaks or two-dimensional streamwise waves can dominate the flow field during the early stages of oblique transition. The growth rates of streaks and two-dimensional waves are dependent on the wavenumber of the initial oblique waves. Streaks dominate the flow for high streamwise wavenumbers, while two-dimensional streamwise waves dominate the flow for low streamwise wavenumbers. Analysis of the turbulent kinetic energy production and the Reynolds stresses reveals that the early stages of the transition differ depending on the wavenumber of the oblique waves. An increase in the initial amplitude of the oblique waves causes a faster transition from laminar flow; however, the growth rates of the streaks and two-dimensional streamwise waves are independent of the initial amplitude. Even though different modes are dominant during the early stages of the O-type transition, the onset of chaotic flow is caused by the breakdown of streak modes.

We investigate the energy transport and heat transfer efficiency in turbulent Rayleigh–Bénard (RB) convection laden with radiatively heated inertial particles. Direct numerical simulations combined with the Lagrangian point-particle mode were carried out in the range of density ratio $854.7\le \rho _p/\rho _0 \le 8547$ and radiation intensity $1\le \phi /\phi _{solar}\le 100$ for both two-dimensional (2-D) and three-dimensional (3-D) simulations. The Rayleigh number ranges from $2\times 10^6$ to $10^8$ for 2-D cases, and is $10^7$ for 3-D cases for $Pr=0.71$. It is found that particles with small density ratio that encounter strong radiation significantly alter the flow momentum transport and fluid heat transfer, so the fluid temperature of bulk is remarkably heated. We then derived the theoretical relation of the Nusselt number for interphase heat transfer in the heated particle-laden RB convection, which reveals that the heat transfer difference between the top and bottom plates stems from the interphase heat transfer. We further found that both the interphase heat transfer and the interphase thermal energy transport exhibit universal properties. They are both increased linearly with the reciprocal of the normalized density ratio. Additionally, both the interphase heat transfer and the interphase thermal energy transport increase linearly with the increase of radiation intensity. The growth rates exhibit specific scaling relations versus Rayleigh number and density ratio. Two different regimes distinguished by the critical density ratio, i.e. the exothermic particle regime and the endothermic particle regime, are observed. We further derived the power-law relation of the critical density ratios versus Rayleigh number and radiation intensity, i.e. $\rho _p/\rho _c \sim (\phi /\phi _{solar})^{1/2}\,Ra^{1/3}$, which is in remarkable agreement with the 3-D simulations.

Displacement flows are common in hydraulic fracturing, as fracking fluids of different composition are injected sequentially in the fracture. The injection of an immiscible fluid at the centre of a liquid-filled fracture results in the growth of the fracture and the outward displacement of the interface between the two liquids. We study the dynamics of the fluid-driven fracture, which is controlled by the competition between viscous, elastic and toughness-related stresses. We use a model experiment to characterize the dynamics of the fracture for a range of mechanical properties of the fractured material and fracturing fluids. We form the liquid-filled pre-fracture in an elastic brittle matrix of gelatin. The displacing liquid is then injected. We record the radius and aperture of the fracture, and the position of the interface between the two liquids. In a typical experiment, the axisymmetric radial viscous flow is accommodated by the elastic deformation and fracturing of the matrix. We model the coupling between elastic deformation, viscous dissipation and fracture propagation, and recover the two fracturing regimes identified for single-fluid injection. For the viscous-dominated and toughness-dominated regimes, we derive scaling equations that describe the crack growth due to a displacement flow and show the influence of the pre-existing fracture on the crack dynamics through a finite initial volume and an average viscosity of the fluids in the fracture.

The vortex force map method for incompressible viscous flows with multiple bodies is derived in this work. The method breaks the fluid force into inertial, vortex-pressure, viscous-pressure and skin-friction components, and it could be used to analyse the fluid dynamic forces on individual bodies in a multi-body assembly. For the first time, we provide a graphical representation of the vortex-pressure force – the vortex force map – for individual bodies in a multi-body assembly. We have shown that the vortex force map in a multi-body set-up differs from single-bodied counterparts from modifications to their hypothetical potential through a nonlinear cross-coupling, and that the inertial and viscous-pressure contributions contain influences from other bodies explicitly. We then demonstrate the multi-body vortex force decomposition method with a wing–flap starting flow problem using computational fluid dynamics data, identifying the positive and negative force-generating critical regions or directions. It is found that the dominant force is the vortex-pressure force, and the force variation against time is closely related to the evolution of the vortex structures. Furthermore, we showed that the existence of another body significantly alters the force contribution roles of vortices in the flow.

This paper studies the instability of two-dimensional magnetohydrodynamic systems on a sphere using analytical methods. The underlying flow consists of a zonal differential rotation and a toroidal magnetic field is present. Semicircle rules that prescribe the possible domain of the wave velocity in the complex plane for general flow and field profiles are derived. The paper then sets out an analytical study of the ‘clamshell instability’, which features field lines on the two hemispheres tilting in opposite directions (Cally, Sol. Phys., vol. 199, 2001, pp. 231–249). An asymptotic solution for the instability problem is derived for the limit of weak shear of the zonal flow, via the method of matched asymptotic expansions. It is shown that when the zonal flow is solid body rotation, there exists a neutral mode that tilts the magnetic field lines, referred to as the ‘tilting mode’. A weak shear of the zonal flow excites the critical layer of the tilting mode, which reverses the tilting direction to form the clamshell pattern and induces the instability. The asymptotic solution provides insights into properties of the instability for a range of flow and field profiles. A remarkable feature is that the magnetic field affects the instability only through its local behaviour in the critical layer.