This paper examines the three-dimensional cellular patterns appearing on wings in subsonic stall and transonic buffet conditions. Unsteady Reynolds-averaged Navier–Stokes simulations are carried out for three-dimensional infinite swept configurations closed by periodic boundary conditions in the spanwise direction. In both flow conditions the occurrence of stall/buffet cells is observed, as well as their convection at a speed proportional to the sweep angle. In transonic buffet conditions, this phenomenon is superimposed to the well-documented two-dimensional buffet instability. These results indicate that the discrepancies between two-dimensional and three-dimensional buffet are caused by the occurrence of buffet cells and that this phenomenon is similar to the one observed at low speed. These phenomena are then studied using global linear stability analysis with the assumption of a periodic flow in the spanwise direction. From these analyses a mode coherent with the two-dimensional buffet is obtained, as well as a mode coherent with two-dimensional vortex shedding in stall conditions. In addition, in both flow conditions an unstable mode reminiscent of stall/buffet cells is observed.

Energy flux plays a key role in analyses of energy-cascading turbulence. In isotropic turbulence, the flux is given by a scalar as a function of the magnitude of the wavenumber. On the other hand, the flux in anisotropic turbulence should be a geometric vector that has a direction as well as a magnitude, and depends not only on the magnitude of the wavenumber but also on its direction. The energy-flux vector in anisotropic turbulence cannot be uniquely determined in a way used for the isotropic flux. In this work, introducing two ansatzes, net locality and efficiency of nonlinear energy transfer, we propose a way to determine the energy-flux vector in anisotropic turbulence using the Moore–Penrose inverse. The energy-flux vector in strongly rotating turbulence is demonstrated based on the energy transfer rate obtained by direct numerical simulations. It is found that the direction of the energy-flux vector is consistent with the prediction of the weak turbulence theory in the wavenumber range dominated by inertial waves. However, the energy flux along the critical wavenumbers predicted by the critical balance in the buffer range between the weak turbulence range and the isotropic Kolmogorov turbulence range is not observed in the present simulations. This discrepancy between the critical balance and the present numerical results is discussed and dissipation is found to play an important role in the energy flux in the buffer range.

Shock reflection experiments are performed to study the large-scale convective mixing created by the forward jetting phenomenon. Experiments are performed at a wedge angle of $\theta _{{w}} = 30^{\circ }$ in nitrogen, propane–oxygen and hexane with incident shock Mach numbers up to $M = 4$. Experiments are complemented by shock-resolved viscous simulations of triple-point reflection in hexane for $M = 2.5$ to $6$. Inviscid simulations are performed over a wider range of parameters. Reynolds numbers up to $Re \lesssim 10^3$ are covered by simulations and Reynolds numbers of $Re \sim 10^5$ are covered by experiments. The study shows that as the isentropic exponent is lowered, and as the Mach number and Reynolds number are increased, the forward jet approaches the Mach stem, forms a vortex, deforms the shock front and in some cases bifurcates the Mach stem. Experiments show that Kelvin–Helmholtz instabilities in the vortex cause large-scale convective mixing behind the Mach stem at low isentropic exponents ($\gamma \le 1.15$). The limits of Mach stem bifurcation (triple Mach–White reflection) in inviscid simulations are plotted in the phase space of $M$–$\theta _{{w}}$–$\gamma$. A maximum isentropic exponent of $\gamma \approx 1.3$ is found beyond which bifurcation does not occur (at $\theta _{{w}} = 30^{\circ }$). This closely matches the boundary between irregular and regular detonation cellular structures.

Large-eddy simulation is combined with the Ffowcs Williams–Hawkings equation to investigate the noise generation by a 10-bladed rotor ingesting the turbulent wake of a circular cylinder in a low-Mach-number flow. Two rotor advance ratios corresponding to zero thrust and a thrusting condition are considered. The computed sound pressure levels agree well with the experimental measurements at Virginia Tech over a wide range of frequencies. The broadband acoustic spectra exhibit a strong tonal peak at the cylinder vortex-shedding frequency, a second peak at the rotor blade passing frequency, and a minor peak at the trailing-edge vortex-shedding frequency. Consistent with experimental results, the rotor at the thrusting advance ratio produces stronger sound than that at zero thrust. The blade acoustic dipole strength increases with the radial distance to the hub until near the blade tip. Fluctuating velocities in the wake are responsible for virtually all the rotor acoustic response except at the blade-passing frequency, where the mean wake velocity defect also makes a strong contribution. Blade-to-blade correlations and coherence of dipole sources are relatively weak. The classical Sears theory is shown to provide a reasonable prediction of the rotor turbulence-ingestion noise at the important mid-frequencies, based on which the appropriate Mach number scaling for the ingestion noise is identified. Distortions of wake turbulence by the rotor are found to be relatively small, and including their effect on the upwash velocity only slightly improves the Sears theory prediction.

A detailed numerical investigation of thermocapillary effects during the melting of phase-change materials in microgravity is presented. The phase-change transition is analysed for the high-Prandtl-number material n-octadecane, which is enclosed in a two-dimensional rectangular container subjected to isothermal conditions along the lateral walls. The progression of the solid/liquid front during the melting leaves a free surface, where the thermocapillary effect acts driving convection in the liquid phase. The nature of the flow found during the melting depends on the container aspect ratio, $\varGamma$, and on the Marangoni number, $Ma$. For large $\varGamma$, this flow initially adopts a steady return flow structure characterised by a single large vortex, which splits into a series of smaller vortices to create a steady multicellular structure (SMC) with increasing $Ma$. At larger values of $Ma$, this SMC undergoes a transition to oscillatory flow through the appearance of a hydrothermal travelling wave (HTW), characterised by the creation of travelling vortices near the cold boundary. For small $\varGamma$, the thermocapillary flow at small to moderate $Ma$ is characterised by an SMC that develops initially within a thin layer near the free surface. At larger times, the SMC evolves into a large-scale steady vortical structure. With increasing applied $Ma$, a complex oscillatory mode is observed. This state, referred to as an oscillatory standing wave (OSW), is characterised by the pulsation of the vortical structure. Finally, for an intermediate $\varGamma$ both HTW and OSW modes can be found depending on $Ma$.

A database of highly resolved direct numerical simulations of three-dimensional isotropic turbulence, with Taylor microscale Reynolds numbers ranging from ${\approx }3$ to 400, and grid sizes up to $2048^3$, is used to analyse the temporal behaviours of spectral transfer and energy that result from low-wavenumber forcing. The temporal behaviours of the energy and energy transfer spectra are analysed using single-time and time-delay statistics. Results show that the energy transfer across a given wavenumber in the inertial range fluctuates by an order of magnitude around its temporal average, and only slow fluctuations have the property of being unidirectional, consistent with classical cascade concepts. All small scales, roughly beyond $k\eta > 0.3$, respond essentially instantly to changes at the large scale.

The unsteady lift of an oscillating airfoil encountering a sinusoidal streamwise gust is experimentally investigated. The sinusoidal streamwise gust is generated by a multiple-fan actively controlled wind tunnel. A two-dimensional airfoil with a NACA0015 profile oscillates in the wind tunnel with a pitch motion frequency of $f_v=1\ \textrm {Hz}$ while the sinusoidal streamwise gust has a different oscillating frequency of $f_{\beta }=1.7\ \textrm {Hz}$. The non-dimensional unsteady lift coefficients determined from surface pressure show the same trends as Greenberg's prediction. Through spectral analysis, the sum frequency $f_{sum}=f_{\beta }+f_v$ and the difference frequency $f_{diff}=|f_{\beta }-f_v|$, proposed by Greenberg, are firstly observed in the experiment. The experimental results are compared with Greenberg's theory in the case of a small amplitude of gust velocity variation $\sigma =0.2$. The results of all cases indicate that the experimental results agree generally well with Greenberg's prediction, while there is a small deviation.

A long-wave model based on lubrication theory is developed for the flow of a viscous liquid film lining the interior of a tube in the presence of an insoluble surfactant on the interface; no thin-film assumption is made. Linear stability analysis identifies two modes; in the absence of base flow, the ‘interface’ mode is the only unstable mode. The growth rates of this mode serve as an accurate predictor of how surfactant concentration increases plug formation time, and the effects of film thickness on this increase are quantified. In the presence of base flow, both the interface mode and ‘surfactant’ mode may be unstable, resulting in a richer variety of free-surface dynamics. In previous work, turning points in families of travelling wave solutions for a falling viscous film lining the interior of a vertical tube with a clean interface have been shown to be a good indicator of $h_c$, the critical thickness past which plugs may form, and this approach is adapted here for flow with surfactant. It is found that turning points in branches of travelling waves that arise from an unstable surfactant mode give an estimate of $h_c$, provided the interface mode is linearly stable. When both modes are unstable, interpretation of these turning points as they relate to plug formation is more complicated. The study concludes by examining the impact of film thickness on growth rates and travelling wave solutions for core–annular flow with surfactant.

The compressible Navier–Stokes–Fourier equations are numerically solved for axially bounded Taylor–Couette flow (TCF) of an ideal gas, with rotating inner cylinder and stationary outer cylinder, to understand the roles of compressibility and finite aspect ratio on the genesis of nonlinear Taylor vortices and the related bifurcation scenario. Restricting to the axisymmetric case in the wide-gap limit, the aspect ratio $\varGamma =h/\delta$ (where $\delta$ is the annular gap between two cylinders and $h$ is the height of the cylinders) is changed quasistatically by varying the height of the cylinders, following the experimental protocol of Benjamin (Proc. R. Soc. Lond. A, vol. 359, 1978b, pp. 27–43). The symmetric even-numbered ($2,4,6,\ldots$) vortices are found at $\varGamma \geq 2$, whereas the asymmetric 2-roll modes (called the single-roll or ‘anomalous’ modes), that break the midplane 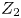$Z_{2}$-symmetry, are uncovered at $\varGamma \leq O(1)$. The phase boundaries of both symmetric and asymmetric rolls and the coexisting regions of different number of rolls are identified in the ($\varGamma , Re$)-plane. These phase diagrams, along with related bifurcation diagrams and various patterns, at finite Mach numbers ($Ma$) are contrasted with their incompressible ($Ma\to 0$) analogues. It is shown that the ‘$1\leftrightarrow 2$’-roll transition in small aspect ratio cylinders is subcritical in compressible TCF in contrast to the supercritical nature of bifurcation in its incompressible counterpart. In general, the gas compressibility has a stabilizing effect on nonlinear Taylor vortices as the underlying phase diagrams in the ($\varGamma , Re$)-plane are shifted to larger values of $Re$ with increasing $Ma$. The stabilizing role of compressibility can be tied to the weakening of the outward jets, which is further aided by the strengthening of the Ekman vortices with increasing Mach number.

Several procedures have been proposed to modify non-objective (observer-dependent) local vortex criteria so that they become objective. These modifications are only justifiable if they are equivalent to applying the original criteria after a generalized (possibly nonlinear) frame change is performed on the flow domain; otherwise, the arguments used in deriving those criteria no longer apply. To examine the feasibility of available objectivization procedures, we derive here necessary and sufficient conditions for the existence of a generalized frame change prescribed pointwise through its Jacobian field. From these conditions we conclude that, of all proposed objectivization approaches in the literature, only the replacement of the spin tensor with the spin-deviation tensor is applicable to generic fluid flows.

The dynamics of flow of a dielectric fluid in a vertical cylindrical annulus with a fixed temperature difference and an increasing alternating electric tension has been investigated using a direct numerical simulation (DNS). The temperature difference imposed on the cylindrical surfaces induces a radial temperature gradient perpendicular to the ground gravity which generates a baroclinic flow ascending near the hot surface and descending near the cold one. The electric field coupled with the permittivity gradient generates a dielectrophoretic buoyancy force which is a source of vorticity. Above a critical value of the electric tension, the flow bifurcates to a pattern of stationary columnar vortices. These columnar vortices which characterize the thermoelectric convection are not axially invariant, in contrast with classical Taylor columns. They bifurcate to regular wave patterns and then to spatio-temporal chaotic patterns when the electric field intensity is increased. The flow and temperature fields, the kinetic energy and the enstrophy of thermoelectric convective regimes are computed for different values of the electric tension.

Liquid foams are, amongst other applications, used to mitigate shock waves. This aspect has received considerable attention at the macroscopic scale. However, the interaction between foam films and shock waves is still poorly understood and may be an important missing local information to build mitigation models. In this paper, we experimentally identify a new process leading to the foam film rupture, which dominates when the film thickness is sufficiently heterogeneous. Using a two-thickness film with a sharp and localised thickness gradient, we record the deformation of the interface between the thick and the thin parts. We observe the growth of an excess liquid area in the thin part and establish an analytical model and scaling laws which account for this phenomenon. Our results in this ideal configuration are consistent with actual rupture processes at stake in heterogeneous foam films.

Heat transport over super-hydrophobic (SHS) and liquid-infused surfaces (LIS) is studied using direct numerical simulations of a turbulent channel flow. The lower wall of the channel consists of either longitudinal or transversal bars with a secondary fluid locked in the cavities between the surface elements. We consider two viscosity ratios between the fluids mimicking SHS and LIS. The thermal diffusivity is varied to assess its effect on thermal performance. We investigate the dependence of heat transfer on the elements pitch-to-height ratio and on the interface dynamics. The interface deformation (dependent upon the surface tension between the two fluids) is fully coupled to the fluid governing equations with the level-set method. Present simulations are consistent with published results about the drag-reducing potential of SHS and LIS in turbulent flow compared to the smooth wall. In the limiting case of infinite surface tension (the interface remains flat and slippery), heat transfer efficiency (heat transfer to drag ratio) can be enhanced compared to a smooth wall. Although the total heat flux is marginally reduced, SHS and LIS with longitudinal ridges achieve a comparatively larger drag reduction, which increases the efficiency. A model is derived from the energy equation to correlate the heat transfer performance with the thermal slip length ($b_\theta$), analogous to the streamwise slip length ($b$) used in the literature to scale drag reduction. Consistently with the model, results show that heat transfer efficiency is larger than for a smooth wall when the thermal slip length is smaller than the streamwise slip length (longitudinal bars). Vice versa, transversal bars present $b/b_\theta <1$ and a smaller heat transfer efficiency than the smooth wall. In the case of finite surface tension, the dynamics of the interface generates a turbulent flux which improves the thermal performance, but tends to decrease the amount of drag reduction. Liquid-infused surfaces are more robust than SHS to the deformation of the interface thanks to the larger viscosity of the secondary fluid and maintain about the same drag reduction as in the infinite surface tension case. For SHS longitudinal bars, simultaneous increase in heat transfer and reduction in drag are observed, leading to an apparent breakdown of the Reynolds analogy. Also in the case of finite surface tension, heat transfer efficiency scales with the relative magnitude of the thermal and streamwise slip lengths. The results suggest a potential expansion of the control space for engineers. Depending on the application, one can reach an optimal combination of heat transfer and drag by tuning the shape of the substrate and the viscosity and diffusivity ratios.

This analysis focuses on the properties of the so-called particle accumulation structures (PAS) in non-cylindrical liquid bridges in normal gravity conditions. In this regard, it follows and integrates the line of inquiry started in Lappa (J. Fluid Mech., vol. 726, 2013, 160) where the main focus was on the effect of high-frequency vibrations. After the discovery (passed almost unnoticed) of a structure (Sasaki et al. Trans. Japan Soc. Mech. Engrs B, vol. 70, 2004) that seems to escape a simple classification on the basis of existing categorizations or paradigms for this type of phenomena, dedicated numerical simulations are carried out in the framework of an integrated Eulerian–Lagrangian approach. Conditions are considered corresponding to isodense and non-isodense particles in a liquid bridge with high aspect ratio, high Prandtl number fluid and hydrostatically deformed interface. Special attention is paid to the very elusive azimuthal wavenumber $m=1$, for which PAS seem to be possible only in a very restricted range of Marangoni numbers. Two distinct families of particle attractors are identified, which coexist in the space of parameters as multiple solutions. We show that the key ingredient needed to unravel the related basins of attraction is the effect of gravity on particles, which may therefore be regarded as an additional mechanism responsible for the formation of these structures in terrestrial liquid bridges.

The coupling between particle–particle and particle–fluid interactions is examined by studying the sedimentation of clouds of spheres in a model cellular flow at a small but finite Reynolds number. The model flow consists of counter-rotating vortices and is aimed at capturing key features of the vortical effects on particles. The dynamics of clouds settling in this vortical flow is investigated through a comparison between experiments and point-particle simulations.

This paper investigates the Reynolds number dependence of a turbulent mixing layer evolving from the Richtmyer–Meshkov instability using a series of direct numerical simulations of a well-defined narrowband initial condition for a range of different Reynolds numbers. The growth rate exponent $\theta$ of the integral width and mixed mass is shown to marginally depend on the initial Reynolds number $Re_0$, as does the minimum value of the molecular mixing fraction $\varTheta$. The decay rates of turbulent kinetic energy and its dissipation rate are shown to decrease with increasing $Re_0$, while the spatial distribution of these quantities is biased towards the spike side of the layer. The normalised dissipation rate $C_{\epsilon }$ and scalar dissipation rate $C_{\chi }$ are calculated and are observed to be approaching a high Reynolds number limit. By fitting an appropriate functional form, the asymptotic values of these two quantities are estimated as $C_{\epsilon }=1.54$ and $C_{\chi }=0.66$. Finally, an evaluation of the mixing transition criterion for unsteady flows is performed, showing that, even for the highest $Re_0$ case, the turbulence in the flow is not yet fully developed. This is despite the observation of a narrow inertial range in the turbulent kinetic energy spectra, with a scaling close to $k^{-3/2}$, where k is the radial wavenumber.

An analysis of the statistics of the nonlinear terms in resolvent analysis is performed in this work for turbulent Couette flow at Reynolds number 400. Data from a direct numerical simulation of a minimal flow unit is used to compute the covariance matrix of the velocity. From the same data, we computed the nonlinear terms of the Navier–Stokes equations (treated as forcing), which allowed us to compute the covariance matrix of the forcing. The quantitative relation between the two covariances via the resolvent operator is confirmed here for the first time, accounting for relevant signal processing issues related to the windowing procedure for frequency-domain quantities. Such exact correspondence allowed the eduction of the most relevant force components for the dominant structures in this flow, which participate in the self-sustaining cycle of turbulence: (i) streamwise vortices and streaks, and (ii) spanwise-coherent fluctuations of spanwise velocity. The results show a dominance by a subset of the nonlinear terms for the prediction of the full statistics of streamwise vortices and streaks; a single term is seen to be dominant for spanwise motions. A relevant feature observed in these cases is that the forcing covariance is dominated by its first eigenfunction, showing that nonlinear terms also have a coherent structure at low frequencies in this flow. Different forcing components are also coherent between them, which leads to constructive and destructive interferences that greatly modify the flow response. These are key features of forcing ‘colour’ for the present flow.

A fully three-dimensional boundary-integral method (BIM) is developed for the interaction of drops, suspended in a uniform far-field flow at small Reynolds number, with arbitrary Lyapunov surfaces. The close approach of fluid interfaces to solid surfaces poses significant challenges for numerical BIM implementations, due to the highly singular behaviour of single- and double-layer boundary integrals. Two new methods are described that generalize the accurate calculation of the highly singular surface integrals used by high-order desingularization techniques. The first method is semi-analytical, and applies to axisymmetric solid obstacles (in an arbitrary three-dimensional configuration). An axisymmetric particle can be divided into a series of characteristic disks along its axis, for which closed-form expressions for single and double layers are derived in terms of elliptic integrals. To accommodate arbitrary smooth surfaces, a multimesh desingularization method is introduced that calculates surface integrals utilizing a hierarchy of embedded mesh resolutions, together with distance-activated mesh interactions. Several particle shapes, including spherocylinders (capsules) and flat plates, are used to represent major classes characteristic of porous media. A droplet approaching a capsule will break up after forming two lobes, connected by a thin filament, on either side of the capsule. The cross-sectional shape of the filament affects lubrication behaviour. A constriction made of two parallel capsules, even of low aspect ratio, significantly retards drop passage compared to two spheres. Trends in drop squeezing between two capsules are summarized over a range of capillary number, viscosity ratio, drop size and capsule length. A constriction of two coplanar plates results in notably different lubrication and squeezing behaviour. Flow rectification is demonstrated for constrictions that are non-symmetrical with respect to flow reversal, for several non-axisymmetric particles.

In the presence of temperature gradients along the gas–liquid interface, a liquid bridge is prone to hydrothermal instabilities. In the case of a coaxial gas stream, in addition to buoyancy and thermocapillary forces, the shear stresses and interfacial heat transfer affect the development of these instabilities. By combining experimental data with three-dimensional numerical simulations, we examine the evolution of hydrothermal waves in a liquid bridge with $Pr=14$ with a gas flow parallel to the interface. The gas moves from the cold to the hot side with a constant velocity of $0.5\ \textrm {m}\ \textrm {s}^{-1}$ and its temperature is the main control parameter of the study. When the thermal stress ${\rm \Delta} T$ exceeds a critical value ${\rm \Delta} T_{cr}$, a three-dimensional oscillatory flow occurs in the system. A stability window of steady flow has been found to exist in the map of dynamical states in terms of gas temperature and applied thermal stress ${\rm \Delta} T$. The study is carried out by tracking the evolution of hydrothermal waves with increasing gas temperature along three distinct paths with constant values of ${\rm \Delta} T$: path 1 is selected to be just above the threshold of instability while path 2 traverses the stability window and path 3 lies above it. We observe a variety of dynamics including standing and travelling waves, determine their dominant and secondary azimuthal wavenumbers, and suggest the mathematical equations describing hydrothermal waves. Multimodal standing waves, coexistence of travelling waves with several wavenumbers rotating in the same or opposite directions are among the most intriguing observations.

Three-dimensional, steady laminar flow structures with mixing, chemical reaction, normal strain and shear strain representative of turbulent combustion are analysed. A mixing layer is subjected to counterflow in the transverse $y$- and $z$-directions providing the important practical interaction of shear-strain rate with normal-strain rate. Larger consequences for mixing rates and burning rates occur than would appear with shear strain or normal strain alone. The three characteristic times for chemical reaction, normal strain and shear strain are cast through two ratios: a Damköhler number based on rate of shear strain and a ratio of rate of normal strain to rate of shear strain. Reduction to a one-dimensional similar form is obtained with density and property variations. A generalization is found extending the Crocco integral for non-unitary Prandtl number and for imposed normal strain. A diffusion flamelet model with combined shear and normal strains is developed. Another similar solution is obtained for a configuration with a dominant diffusion flame and a weaker fuel-rich premixed flame. A conserved scalar is cast as the independent variable giving an alternative description. The imposed normal strain decreases mixing-layer thickness and increases scalar gradients and transport rates. Diffusion control is possible for partially premixed flames in the multi-branched flame situation. The imposition of shear strain and thereby vorticity on the counterflow can have a substantial consequence, indicating the need for flamelet models with both shear strain and normal strain.