Hydrodynamic forces acting on a neutrally buoyant spherical particle immersed in a wall-bounded axisymmetric stagnation-point flow (Hiemenz–Homann flow) are predicted, based on a suitable form of the reciprocal theorem. An approximate algebraic form of the undisturbed velocity field is set up, mimicking the gradual transition of the actual carrying flow throughout the boundary layer, from a pure linear straining flow in the bulk to a parabolic flow at the wall. The particle Reynolds number is assumed to be small and predictions based on the creeping-flow assumption are first derived. Then, inertial corrections are computed, assuming that the particle stands close enough to the wall for the latter to be in the inner region of the disturbance. Predictions for the time-dependent slip velocity between the particle and ambient fluid are obtained in the form of a differential equation, first assuming that the particle moves along the flow symmetry axis, then extending the analysis to particles released at an arbitrary radial position. In the former case, these predictions are compared with results provided by numerical simulations. When the strain-based Reynolds number (built on the particle radius and strain rate in the bulk) exceeds $0.1$, finite-inertia effects due to particle–wall interactions and to the relative acceleration between the particle and fluid are found to substantially modify the way the slip velocity varies with the distance to the wall.

We analyse the model problem of rigid, spherical pendula impacting on rubber membranes at different Reynolds numbers to understand the contact dynamics in deformable bodies in a viscous fluid. We have investigated the problem both by laboratory and numerical experiments and a new contact model has been developed to perform the simulations. We have found that the collision dynamics depends on many parameters, the most important ones being the impact Stokes number ($St$) and the ratio of the membrane thickness ($e$) to sphere diameter ($2R$). For $e/(2R)=0.1$ the pendulum rebounds for $St \geqslant 18$ and this threshold increases as the membrane thickness decreases. Also, the membrane surface affects the dynamics of the impact by delaying the rebound for smaller membranes.

Circular milling, a stunning manifestation of collective motion, is found across the natural world, from fish shoals to army ants. It has been observed recently that the plant-animal worm Symsagittifera roscoffensis exhibits circular milling behaviour, both in shallow pools at the beach and in Petri dishes in the laboratory. Here we investigate this phenomenon experimentally and theoretically, from a fluid dynamical viewpoint, focusing on the effect that an established circular mill has on the surrounding fluid. Unlike systems such as confined bacterial suspensions and collections of molecular motors and filaments that exhibit spontaneous circulatory behaviour, and which are modelled as force dipoles, the front–back symmetry of individual worms precludes a stresslet contribution. Instead, singularities such as source dipoles and Stokes quadrupoles are expected to dominate. We analyse a series of models to understand the contributions of these singularities to the azimuthal flow fields generated by a mill, in light of the particular boundary conditions that hold for flow in a Petri dish. A model that treats a circular mill as a rigid rotating disc that generates a Stokes flow is shown to capture basic experimental results well, and gives insights into the emergence and stability of multiple mill systems.

The spreading under surface tension and gravity of a droplet of yield-stress fluid over a thin film of the same material is studied. The droplet converges to a final equilibrium shape once the driving stresses inside the droplet fall below the yield stress. Scaling laws are presented for the final radius and complemented with an asymptotic analysis for shallow droplets. Moreover, numerical simulations using the volume-of-fluid method and a regularized constitutive law, and experiments with an aqueous solution of Carbopol, are presented.

Electrohydrodynamics of drops is a classic fluid mechanical problem where deformations and microscale flows are generated by application of an external electric field. In weak fields, electric stresses acting on the drop surface drive quadrupolar flows inside and outside and cause the drop to adopt a steady axisymmetric shape. This phenomenon is best explained by the leaky-dielectric model under the premise that a net surface charge is present at the interface while the bulk fluids are electroneutral. In the case of dielectric drops, increasing the electric field beyond a critical value can cause the drop to start rotating spontaneously and assume a steady tilted shape. This symmetry-breaking phenomenon, called Quincke rotation, arises due to the action of the interfacial electric torque countering the viscous torque on the drop, giving rise to steady rotation in sufficiently strong fields. Here, we present a small-deformation theory for the electrohydrodynamics of dielectric drops for the complete Melcher–Taylor leaky-dielectric model in three dimensions. Our theory is valid in the limits of strong capillary forces and highly viscous drops and is able to capture the transition to Quincke rotation. A coupled set of nonlinear ordinary differential equations for the induced dipole moments and shape functions are derived whose solution matches well with experimental results in the appropriate small-deformation regime. Retention of both the straining and rotational components of the flow in the governing equation for charge transport enables us to perform a linear stability analysis and derive a criterion for the applied electric field strength that must be overcome for the onset of Quincke rotation of a viscous drop.

For a small sessile or pendant droplet it is generally assumed that gravity does not play any role once the Bond number is small. This is even assumed for evaporating binary sessile or pendant droplets, in which convective flows can be driven due to selective evaporation of one component and the resulting concentration and thus surface tension differences at the air–liquid interface. However, recent studies have shown that in such droplets gravity indeed can play a role and that natural convection can be the dominant driving mechanism for the flow inside evaporating binary droplets (Edwards et al., Phys. Rev. Lett., vol. 121, 2018, 184501; Li et al., Phys. Rev. Lett., vol. 122, 2019, 114501). In this study, we derive and validate a quasi-stationary model for the flow inside evaporating binary sessile and pendant droplets, which successfully allows one to predict the prevalence and the intriguing interaction of Rayleigh and/or Marangoni convection on the basis of a phase diagram for the flow field expressed in terms of the Rayleigh and Marangoni numbers.

We study the pairwise interactions of drops in an applied uniform DC electric field within the framework of the leaky dielectric model. We develop three-dimensional numerical simulations using the boundary integral method and an analytical theory assuming small drop deformations. We apply the simulations and the theory to explore the electrohydrodynamic interactions between two identical drops with arbitrary orientation of their line of centres relative to the applied field direction. Our results show a complex dynamics depending on the conductivities and permittivities of the drops and suspending fluids, and the initial drop pair alignment with the applied electric field.

Capsules, composed of a liquid core protected by a thin deformable membrane, offer high-potential applications in many fields of industry such as bioengineering. One of their limitations comes from the absence of models of capsule damage and/or rupture when they are subjected to an external flow. To assess when rupture is initiated, we develop a fluid–structure interaction (FSI) numerical model of a capsule in Stokes flow that accounts for potential damage of the capsule membrane. We consider the framework of continuum damage mechanics and model the membrane with an isotropic brittle damage model, in which the membrane damage state depends on the history of loading. The FSI problem is solved by coupling the finite element method, to solve for the membrane deformation, with the boundary integral method, to solve for the inner and outer fluid flows. The model is applied to an initially spherical capsule subjected to a simple shear flow. Damage initiates at a critical value of the capillary number, ratio of the fluid viscous forces to the membrane elastic forces and rupture occurs at a higher capillary number, when it reaches a threshold value. The material parameters introduced in the damage model do not influence the mode of damage but only the values of the critical and threshold capillary numbers. When the capillary number is larger than the critical value, damage develops in the two symmetric central regions containing the vorticity axis. It is indeed in these regions that the internal tensions are the highest on the membrane.

A concentrated, vertical monolayer of identical spherical squirmers, which may be bottom heavy, and which are subjected to a linear shear flow, is modelled computationally by two different methods: Stokesian dynamics, and a lubrication-theory-based method. Inertia is negligible. The aim is to compute the effective shear viscosity and, where possible, the normal stress differences as functions of the areal fraction of spheres 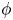$\phi$, the squirming parameter $\beta$ (proportional to the ratio of a squirmer's active stresslet to its swimming speed), the ratio 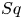$Sq$ of swimming speed to a typical speed of the shear flow, the bottom-heaviness parameter 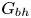$G_{bh}$, the angle 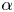$\alpha$ that the shear flow makes with the horizontal and two parameters that define the repulsive force that is required computationally to prevent the squirmers from overlapping when their distance apart is less than a critical value. The Stokesian dynamics method allows the rheological quantities to be computed for values of 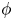$\phi$ up to 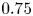$0.75$; the lubrication-theory method can be used for 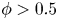$\phi > 0.5$. For non-bottom-heavy squirmers, which are unaffected by gravity, the effective shear viscosity is found to increase more rapidly with 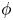$\phi$ than for inert spheres, whether the squirmers are pullers (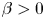$\beta > 0$) or pushers (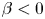$\beta < 0$); it also varies with 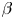$\beta$, although not by very much. However, for bottom-heavy squirmers the behaviour for pullers and pushers as 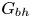$G_{bh}$ and 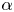$\alpha$ are varied is very different, since the viscosity can fall even below that of the suspending fluid for pushers at high 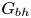$G_{bh}$. The normal stress differences, which are small for inert spheres, can become very large for bottom-heavy squirmers, increasing with 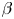$\beta$, and varying dramatically as the orientation 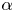$\alpha$ of the flow is varied from 0 to 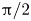${\rm \pi} /2$. A major finding is that, despite very different assumptions, the two methods of computation give overlapping results for viscosity as a function of 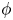$\phi$ in the range 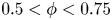$0.5 < \phi < 0.75$. This suggests that lubrication theory, based on near-field interactions alone, contains most of the relevant physics, and that taking account of interactions with more distant particles than the nearest is not essential to describe the dominant physics.

A miscible horizontal interface separating two solutions of different solutes in the gravity field can deform into convective finger structures due to the Rayleigh–Taylor (RT) instability, or the double-diffusive (DD) and diffusive-layer-convection (DLC) instabilities, triggered by differential diffusion of the solutes. We analyse here numerically the nonlinear dynamics of these buoyancy-driven instabilities in porous medium flows by an integration of Darcy's law coupled to advection–diffusion equations for the concentrations of the two solutes. After a diffusive growth, the mixing length $L$, defined as the vertical extent of the mixing zone, starts to grow linearly when convection sets in. We compute the mixing velocity $U$ as the slope of this linear growth. In the one-species RT regime, $U$ is proportional to ${\rm \Delta} \rho _0$, the initial density difference between the two layers. In the two-species problem, differential diffusion effects can induce non-monotonic density profiles characterised by an adverse density difference, defined as the density jump across the spatial domain where the density decreases along the direction of gravity. We find that, in the parameter space spanned by the buoyancy ratio $R$, and the ratio $\delta$ of diffusion coefficients of the two species, the mixing velocity scales linearly with this dynamic density difference. It is computed analytically from the diffusive base-state density profile and can be significantly larger than ${\rm \Delta} \rho _0$. Our results evidence the possibility of controlling the mixing of RT, DD and DLC instabilities in two-species stratifications by a careful choice of the nature and thus diffusivity of the species involved.

We consider the solidification of idealised two-component mixtures comprising a solvent or suspending fluid and dissolved solute molecules or suspended colloidal particles, each considered as hard spheres. We review some fundamental thermodynamic ideas regarding relative motion between species and phase equilibria in such mixtures to show how the related solid–liquid phase diagrams depend on the size of the spheres. Using similarity solutions, we first describe freezing of the solvent to form a pure solid (here referred to as ‘ice’), with the solute rejected from the solid forming a boundary layer or dense particle layer ahead of the freezing front. We extend ideas of constitutional supercooling to the case of colloidal suspensions and show that, for a given temperature difference driving solidification, constitutional supercooling occurs only for an intermediate range of particle sizes. Constitutional supercooling promotes the formation of a mushy layer in which segregated ice separates regions of concentrated solute or particles on the microscale. We formulate a continuum model of the mushy layer that relies on a key observation that the regelative motion of concentrated clusters of particles is independent of the size and geometry of the cluster. Our modelling begins with a description of relative motion as a Fickian diffusive process. However, at high particle concentrations, we show that it is more convenient and more computationally tractable to use an equivalent formulation in terms of Darcy flow of the solvent. Within a mushy layer these diffusive fluxes correspond directly to the regelative flux of particle clusters at a rate determined by the local temperature and temperature gradient.

We derive expressions for the leading-order far-field flows generated by externally driven and active (swimming) colloids at planar fluid–fluid interfaces. We consider colloids adjacent to the interface or adhered to the interface with a pinned contact line. The Reynolds and capillary numbers are assumed much less than unity, in line with typical micron-scale colloids involving air– or alkane–aqueous interfaces. For driven colloids, the leading-order flow is given by the point-force (and/or torque) response of this system. For active colloids, the force-dipole (stresslet) response occurs at leading order. At clean (surfactant-free) interfaces, these hydrodynamic modes are essentially a restricted set of the usual Stokes multipoles in a bulk fluid. To leading order, driven colloids exert Stokeslets parallel to the interface, while active colloids drive differently oriented stresslets depending on the colloid's orientation. We then consider how these modes are altered by the presence of an incompressible interface, a typical circumstance for colloidal systems at small capillary numbers in the presence of surfactant. The leading-order modes for driven and active colloids are restructured dramatically. For driven colloids, interfacial incompressibility substantially weakens the far-field flow normal to the interface; the point-force response drives flow only parallel to the interface. However, Marangoni stresses induce a new dipolar mode, which lacks an analogue on a clean interface. Surface-viscous stresses, if present, potentially generate very long-ranged flow on the interface and the surrounding fluids. Our results have important implications for colloid assembly and advective mass transport enhancement near fluid boundaries.

We revisit the dynamics of a thick liquid film flowing down a vertical fibre. Instead of deriving a long-wave model, we directly solve the Navier–Stokes equations using a domain mapping technique and the exact steady travelling wave solutions are explored using a dynamical systems theory approach. Three distinct flow regimes, labelled ‘a’, ‘b’ and ‘c’, observed in previous experiments (Kliakhandler et al., J. Fluid Mech., vol. 429, 2001, pp. 381–390) are investigated. Flow regime ‘a’ refers to a steady flow state in which large droplets are separated by a long thin film. Flow regime ‘b’ is a necklace-like flow. In flow regime ‘c’, a cyclic process of droplet coalescence and breakup was observed. By matching the mean flow rates of the travelling wave solutions and experimental data, our travelling wave solutions show an excellent agreement with flow regimes ‘a’ and ‘b’. The time-periodic flow regime ‘c’ is compared with direct numerical simulation of the Navier–Stokes equations. A snapshot of the simulation shows a remarkable similarity to an experimental image and the discrepancy of mean wave speed and maximal wave height between our numerical simulation and experimental data is negligible.

We present a numerical study of the dynamics of an elastic fibre in a shear flow at low Reynolds number, and seek to understand several aspects of the fibre's motion using the equations for slender-body theory coupled to the elastica. The numerical simulations are performed in the bead-spring framework including hydrodynamic interactions in two theoretical schemes: the generalized Rotne–Prager–Yamakawa model and a multipole expansion corrected for lubrication forces. In general, the two schemes yield similar results, including for the dominant scaling features of the shape that we identify. In particular, we focus on the evolution of an initially straight fibre oriented in the flow direction and show that the time scales of fibre bending, curling and rotation, which depend on its length and stiffness, determine the overall motion and evolution of the shapes. We document several characteristic time scales and curvatures representative of the shape that vary as power laws of the bending stiffness and fibre length. The numerical results are further supported by an interpretation using an elastica model.

The freezing of a water rivulet begins with a water thread flowing over a very cold surface, is naturally followed by the growth of an ice layer and ends up with a water rivulet flowing on a static thin ice wall. The structure of this final ice layer presents a surprising linear shape that thickens with the distance. This paper presents a theoretical model and experimental characterisation of the ice growth dynamics, the final ice shape and the temperature fields. In a first part, we establish a two-dimensional model, based on the advection–diffusion heat equations, that allows us to predict the shape of the ice structure and the temperature fields in both the water and the ice. Then, we study experimentally the formation of the ice layer and we show that both the transient dynamics and the final shape are well captured by the model. In a last part, we characterise experimentally the temperature fields in the ice and in the water, using an infrared camera. The model shows an excellent agreement with the experimental fields. In particular, it predicts well the linear decrease of the water surface temperature observed along the plane, confirming that the final ice shape is a consequence of the interaction between the thermal boundary layer and the free surface.

The sedimentation dynamics of a dilute suspension of non-Brownian spheres is experimentally examined at small particle Reynolds numbers but at Reynolds numbers based on the container size extending up to the small-but-finite inertial regime. While the long-time velocity fluctuations are independent of the Reynolds number in the Stokes regime, they are seen to decrease with increasing Reynolds number above a critical container Reynolds number of approximately $0.1$, and more precisely to vary as a power $-0.1$ of the Reynolds number. The microstructure of the suspension is also seen to evolve with increasing Reynolds number and to depart from random positioning as it becomes more sub-homogeneous and disordered.

Motivated by the desire to understand complex transient behaviour in fluid flows, we study the dynamics of an air bubble driven by the steady motion of a suspending viscous fluid within a Hele-Shaw channel with a centred depth perturbation. Using both experiments and numerical simulations of a depth-averaged model, we investigate the evolution of an initially centred bubble of prescribed volume as a function of flow rate and initial shape. The experiments exhibit a rich variety of organised transient dynamics, involving bubble breakup as well as aggregation and coalescence of interacting neighbouring bubbles. The long-term outcome is either a single bubble or multiple separating bubbles, positioned along the channel in order of increasing velocity. Up to moderate flow rates, the life and fate of the bubble are reproducible and can be categorised by a small number of characteristic behaviours that occur in simply connected regions of the parameter plane. Increasing the flow rate leads to less reproducible time evolutions with increasing sensitivity to initial conditions and perturbations in the channel. Time-dependent numerical simulations that allow for breakup and coalescence are found to reproduce most of the dynamical behaviour observed experimentally, including enhanced sensitivity at high flow rate. An unusual feature of this system is that the set of steady and periodic solutions can change during temporal evolution because both the number of bubbles and their size distribution evolve due to breakup and coalescence events. Calculation of stable and unstable solutions in the single- and two-bubble cases reveals that the transient dynamics is orchestrated by weakly unstable solutions of the system that can appear and disappear as the number of bubbles changes.

The interaction between heavy particles with high Stokes number ($St$) and the wall, known as the particle–wall (P–W) process, widely exists in natural and engineering two-phase flows, whereas its effects on particle-laden flows and the large-scale/very large-scale turbulent motions (VLSM) remain unclear. In this paper, two types of wind-blown sand-laden flows were experimentally designed and investigated by keeping the same free stream velocity, flow Reynolds number and particle $St$ number. In the first type, sand particles were directly blown from a sand bed at the bottom wall of the wind tunnel, and the P–W process occurred in the whole wall-normal region of the sand-laden flow. In the second type, sand particles were released from a feeder at the top wall of wind tunnel, and the P–W process was only present in a lower wall-normal region. Simultaneous two-phase particle image/tracking velocimetry measurements were conducted for uncovering the characteristics of turbulent structures in the particle-laden turbulent boundary layers. The results confirmed that the VLSM with streamwise scales exceeding $3\delta$ ($\delta$ is boundary layer thickness) above a certain height exist in both types of the sand-laden flows and could be significantly affected by the P–W process. That is, in the region without the P–W process, the presence of sand particles can enlarge the VLSM, while in the region with the P–W process, the VLSM are substantially reduced in size or even destroyed. The reduction degree is found to be closely related to the strength of the P–W process.

Flowing granular materials exhibit several features that distinguish them from molecular fluids. A prominent feature is dilatancy, or volume deformation caused by shear deformation. Its significance in sustained flow has not been much appreciated, as its effect was thought to be confined to thin shear layers. However, it was demonstrated recently by Krishnaraj & Nott (Nat. Commun., vol. 7, 2016, 10630) that dilatancy drives a large-scale secondary flow in a cylindrical Couette device. They hypothesized that the combination of shear and gravity, when their directions are non-collinear, is necessary for the occurrence of the secondary flow. In this paper we investigate the phenomenon by considering a more complex primary flow generated in a split-bottom Couette device, wherein a part of the base of the container filled with a granular material is translated or rotated. It is known from previous studies that the height to which the material is filled determines the shape and extent of the shearing region in the primary flow. We show that the fill height also determines the form of the secondary flow, and argue that the two are intricately coupled and evolve together. Though the secondary flow is more complex than in a cylindrical Couette device, the mechanism is indeed what Krishnaraj & Nott hypothesized: the combined effect of dilatancy driven expansion, and gravity-driven flow down regions of low density. Unlike fluid instabilities that are typically driven by inertia, the secondary flow occurs at arbitrarily low shear rate and appears to be an integral part of the kinematic response.

How to design an optimal biomedical flow device to minimise trapping of undesirable biological solutes/debris and/or enhance their washout is a pertinent but complex question. While biomedical devices often utilise externally driven flows to enhance washout, the presence of vortices – arising as a result of fluid flows within cavities – hinder washout by trapping debris. Motivated by this, we solve the steady, incompressible Navier–Stokes equations for flow through channels into and out of a two-dimensional cavity. In endourology, the presence of vortices – enhanced by flow symmetry breaking – has been linked to long washout times of kidney stone dust in the renal pelvis cavity, with dust transport modelled via advection and diffusion of a passive tracer (Williams et al., J. Fluid Mech., vol. 902, 2020, A16). Here, we determine the inflow and outflow channel geometries that minimise washout times. For a given flow field $\boldsymbol {u}$, vortices are characterised by regions where $\det \boldsymbol {\nabla }\boldsymbol {u} > 0$ (Jeong & Hussain, J. Fluid Mech., vol. 285, 1995, pp. 69–94). Integrating a smooth form of $\max (0, \det \boldsymbol {\nabla }\boldsymbol {u})$ over the domain provides an objective to minimise recirculation zones (Kasumba & Kunisch, Comput. Optim. Appl., vol. 52, 2012, pp. 691–717). We employ adjoint-based shape optimisation to identify inflow and outflow channel geometries that reduce this objective. We show that a reduction in the vortex objective correlates with reduced washout times. We additionally show how multiple solutions to the flow equations lead to solution branch switching during the optimisation routine by characterising the change in solution bifurcation structure with the change in inflow/outflow channel geometry.