Celebrating the life and work of Professor George K. Batchelor FRS Founding Editor of the Journal of Fluid Mechanics.

Graphical Abstract © Mark Hallworth. Reproduced with Permission.

An informal introduction is provided to a range of topics in fluid dynamics having a topological character. These topics include flows with boundary singularities, Lagrangian chaos, frozen-in fields, magnetohydrodynamic analogies, fast- and slow-dynamo mechanisms, magnetic relaxation, minimum-energy states, knotted flux tubes, vortex reconnection and the finite-time singularity problem. The paper concludes with a number of open questions concerning the above topics.

Extreme events in turbulent flow are associated with intense stretching of concentrated vortices, intermittent in both space and time. The occurrence of such events has been investigated in a turbulent flow driven by counter-rotating propellors (Debue et al., J. Fluid Mech., 2021), and local flow structures have been identified. Interesting theoretical problems arise in relation to this work; these are briefly considered in this focus paper.

This article shows how George Batchelor, in close collaboration with Dietrich Küchemann, succeeded in founding Euromech, the European Mechanics Committee, in the sixties during the rise of the ‘Cold War’. It is argued that the initial success of Euromech was due to the organisation of Euromech Colloquia, i.e. meetings of at most 50 scientists, focussing on a sufficiently specialised topic and leaving ample time for informal discussions. The maturation of Euromech into the European Mechanics Society in the nineties is then analysed. This transition was in part made necessary by the creation of five series of large European Conferences in Fluid and Solid Mechanics, Turbulence, Nonlinear Oscillations and Mechanics of Materials. The collective action of George Batchelor and a few outstanding European scientists is brought to light.

We have conducted an extensive study of the scaling properties of small scale turbulence using both numerical and experimental data of a flow in the same von Kármán geometry. We have computed the wavelet structure functions, and the structure functions of the vortical part of the flow and of the local energy transfers. We find that the latter obey a generalized extended scaling, similar to that already observed for the wavelet structure functions. We compute the multi-fractal spectra of all the structure functions and show that they all coincide with each other, providing a local refined hypothesis. We find that both areas of strong vorticity and strong local energy transfer are highly intermittent and are correlated. For most cases, the location of local maximum of the energy transfer is shifted with respect to the location of local maximum of the vorticity. We, however, observe a much stronger correlation between vorticity and local energy transfer in the shear layer, that may be an indication of a self-similar quasi-singular structure that may dominate the scaling properties of large order structure functions.

The nonlinear mechanism in the self-sustaining process (SSP) of wall-bounded turbulence is investigated. Resolvent analysis is used to identify the principal forcing mode that produces the maximum amplification of the velocities in numerical simulations of the minimal channel for the buffer layer and a modified logarithmic (log) layer. The wavenumbers targeted in this study are those of the fundamental mode, which is infinitely long in the streamwise direction and once-periodic in the spanwise direction. The identified mode is then projected out from the nonlinear term of the Navier–Stokes equations at each time step from the simulation of the corresponding minimal channel. The results show that the removal of the principal forcing mode of the fundamental wavenumber can inhibit turbulence in both the buffer and log layer, with the effect being greater in the buffer layer. Removing other modes instead of the principal mode of the fundamental wavenumber only marginally affects the flow. Closer inspection of the dyadic interactions in the nonlinear term shows that contributions to the principal forcing mode come from a limited set of wavenumber interactions. Using conditional averaging, the flow structures that are responsible for generating the nonlinear interaction to self-sustain turbulence are identified as spanwise rolls interacting with oblique streaks. This method, based on the equations of motion, validates the similarities in the SSP of the buffer and log layer, and characterises the underlying quadratic interactions in the SSP of the minimal channel.

Laminar–turbulent transition in boundary layers is characterized by the generation and metamorphosis of flow structures. However, the process of the evolution from a three-dimensional (3-D) wave to a $\varLambda$-vortex is not fully understood. In order to develop a deeper understanding of the spatiotemporal wave-warping process, we present numerical studies of both K-regime transition and bypass transition. A qualitative comparison of flow visualizations between a K-regime zero pressure gradient (ZPG) case and an adverse pressure gradient (APG) case is done, based on the method of Lagrangian tracking of marked particles. In bypass transition, the development of a 3-D wave packet before the breakdown into a turbulent spot was visualized for both the linear and nonlinear stages. The underlying vortex dynamics was investigated using a proposed method of Lagrangian-averaged enstrophy. The study illustrates that a $\varLambda$-vortex develops from a 3-D warped wave front (WWF), which undergoes multiple folding processes. It is observed that the APG case undergoes a more rapid evolution, precipitating a stronger viscous–inviscid interaction within the boundary layer. It is hypothesized that the amplification and lift-up of a 3-D wave causes the development of high-shear layers and a WWF. In order to seek a relationship between transitional and turbulent boundary layers, Lagrangian methods were also applied to an experimental data set from a turbulent boundary layer at low Reynolds number. Similarity of flow behaviours are observed, which further supports the hypothesis that the amplification of a 3-D wave precipitates low-speed streaks and rotational structures in wall-bounded flows.

Townsend (J. Fluid Mech., vol. 11, issue 1, 1961, pp. 97–120) introduced the concept of active and inactive motions for wall-bounded turbulent flows, where the active motions are solely responsible for producing the Reynolds shear stress, the key momentum transport term in these flows. While the wall-normal component of velocity is associated exclusively with the active motions, the wall-parallel components of velocity are associated with both active and inactive motions. In this paper, we propose a method to segregate the active and inactive components of the two-dimensional (2-D) energy spectrum of the streamwise velocity, thereby allowing us to test the self-similarity characteristics of the former which are central to theoretical models for wall turbulence. The approach is based on analysing datasets comprising two-point streamwise velocity signals coupled with a spectral linear stochastic estimation based procedure. The data considered span a friction Reynolds number range $Re_{\tau }\sim {{O}}$($10^3$) – ${{O}}$($10^4$). The procedure linearly decomposes the full 2-D spectrum (${\varPhi }$) into two components, ${\varPhi }_{ia}$ and ${\varPhi }_{a}$, comprising contributions predominantly from the inactive and active motions, respectively. This is confirmed by ${\varPhi }_{a}$ exhibiting wall scaling, for both streamwise and spanwise wavelengths, corresponding well with the Reynolds shear stress cospectra reported in the literature. Both ${\varPhi }_{a}$ and ${\varPhi }_{ia}$ are found to depict prominent self-similar characteristics in the inertially dominated region close to the wall, suggestive of contributions from Townsend's attached eddies. Inactive contributions from the attached eddies reveal pure $k^{-1}$-scaling for the associated one-dimensional spectra (where $k$ is the streamwise/spanwise wavenumber), lending empirical support to the attached eddy model of Perry & Chong (J. Fluid Mech., vol. 119, 1982, pp. 173–217).

By analysing the Karman–Howarth equation for filtered-velocity fields in turbulent flows, we show that the two-point correlation between the filtered strain-rate and subfilter stress tensors plays a central role in the evolution of filtered-velocity correlation functions. Two-point correlation-based statistical a priori tests thus enable rigorous and physically meaningful studies of turbulence models. Using data from direct numerical simulations of isotropic and channel flow turbulence, we show that local eddy-viscosity models fail to exhibit the long tails observed in the real subfilter stress–strain-rate correlation functions. Stronger non-local correlations may be achieved by defining the eddy-viscosity model based on fractional gradients of order $0<\alpha <1$ (where $\alpha$ is the fractional gradient order) rather than the classical gradient corresponding to $\alpha =1$. Analyses of such correlation functions are presented for various orders of the fractional-gradient operators. It is found that in isotropic turbulence fractional derivative order $\alpha \sim 0.5$ yields best results, while for channel flow $\alpha \sim 0.2$ yields better results for the correlations in the streamwise direction, even well into the core channel region. In the spanwise direction, channel flow results show significantly more local interactions. The overall results confirm strong non-locality in the interactions between subfilter stresses and resolved-scale fluid deformation rates, but with non-trivial directional dependencies in non-isotropic flows. Hence, non-local operators thus exhibit interesting modelling capabilities and potential for large-eddy simulations although more developments are required, both on the theoretical and computational implementation fronts.

We present a framework for predicting the interactions between motion at a single scale and the underlying stress fluctuations in wall turbulence, derived from approximations to the Navier–Stokes equations. The dynamical equations for an isolated scale and stress fluctuations at the same scale are obtained from a decomposition of the governing equations and formulated in terms of a transfer function between them. This transfer function is closely related to the direct correlation coefficient of Duvvuri & McKeon (J. Fluid Mech., vol. 767, 2015, R4), and approximately to the amplitude modulation coefficient described in Mathis et al. (J. Fluid Mech., vol. 628, 2009, pp. 311–337), by consideration of interactions between triadically consistent scales. In light of the agreement between analysis and observations, the modelling approach is extended to make predictions concerning the relationship between very-large motions and small-scale stress in the logarithmic region of the mean velocity. Consistent with experiments, the model predicts that the zero-crossing height of the amplitude modulation statistic coincides with the wall-normal location of the very large-scale peak in the one-dimensional premultiplied spectrum of streamwise velocity fluctuations, the critical layer location for the very large-scale motion. Implications of fixed phase relationships between small-scale stresses and larger isolated scales for closure schemes are briefly discussed.

Despite the nonlinear nature of turbulence, there is evidence that part of the energy-transfer mechanisms sustaining wall turbulence can be ascribed to linear processes. The different scenarios stem from linear stability theory and comprise exponential instabilities, neutral modes, transient growth from non-normal operators and parametric instabilities from temporal mean flow variations, among others. These mechanisms, each potentially capable of leading to the observed turbulence structure, are rooted in simplified physical models. Whether the flow follows any or a combination of them remains elusive. Here, we evaluate the linear mechanisms responsible for the energy transfer from the streamwise-averaged mean flow ($\boldsymbol {U}$) to the fluctuating velocities ($\boldsymbol {u}'$). To that end, we use cause-and-effect analysis based on interventions: manipulation of the causing variable leads to changes in the effect. This is achieved by direct numerical simulation of turbulent channel flows at low Reynolds number, in which the energy transfer from $\boldsymbol {U}$ to $\boldsymbol {u}'$ is constrained to preclude a targeted linear mechanism. We show that transient growth is sufficient for sustaining realistic wall turbulence. Self-sustaining turbulence persists when exponential instabilities, neutral modes and parametric instabilities of the mean flow are suppressed. We further show that a key component of transient growth is the Orr/push-over mechanism induced by spanwise variations of the base flow. Finally, we demonstrate that an ensemble of simulations with various frozen-in-time $\boldsymbol {U}$ arranged so that only transient growth is active, can faithfully represent the energy transfer from $\boldsymbol {U}$ to $\boldsymbol {u}'$ as in realistic turbulence. Our approach provides direct cause-and-effect evaluation of the linear energy-injection mechanisms from $\boldsymbol {U}$ to $\boldsymbol {u}'$ in the fully nonlinear system and simplifies the conceptual model of self-sustaining wall turbulence.

We study the three-dimensional structure of turbulent velocity fields around extreme events of local energy transfer in the dissipative range. Velocity fields are measured by tomographic particle velocimetry at the centre of a von Kármán flow with resolution reaching the Kolmogorov scale. The characterization is performed through both direct observation and an analysis of the velocity gradient tensor invariants at the extremes. The conditional average of local energy transfer on the second and third invariants seems to be the largest in the sheet zone, but the most extreme events of local energy transfer mostly correspond to the vortex stretching topology. The direct observation of the velocity fields allows for identification of three different structures: the screw and roll vortices, and the U-turn. They may correspond to a single structure seen at different times or in different frames of reference. The extreme events of local energy transfer come along with large velocity and vorticity norms, and the structure of the vorticity field around these events agrees with previous observations of numerical works at similar Reynolds numbers.

This work shows how the early stages of perturbation growth in a viscosity-stratified flow are different from those in a constant-viscosity flow, and how nonlinearity is a crucial ingredient. We derive the viscosity-varying adjoint Navier–Stokes equations, where gradients in viscosity force both the adjoint momentum and the adjoint scalar. By the technique of direct-adjoint looping, we obtain the nonlinear optimal perturbation which maximises the perturbation kinetic energy of the nonlinear system. While we study three-dimensional plane Poiseuille (channel) flow with the walls at different temperatures, and a temperature-dependent viscosity, our findings are general for any flow with viscosity variations near walls. The Orr and modified lift-up mechanisms are in operation at low and high perturbation amplitudes, respectively, at our subcritical Reynolds number. The nonlinear optimal perturbation contains more energy on the hot (less-viscous) side, with a stronger initial lift-up. However, as the flow evolves, the important dynamics shifts to the cold (more-viscous) side, where wide high-speed streaks of low viscosity grow and persist, and strengthen the inflectional quality of the velocity profile. We provide a physical description of this process and show that the evolution of the linear optimal perturbation misses most of the physics. The Prandtl number does not qualitatively affect the findings at these times. The study of nonlinear optimal perturbations is still in its infancy, and viscosity variations are ubiquitous. We hope that this first work on nonlinear optimal perturbation with viscosity variations will lead to wider studies on transition to turbulence in these flows.

In this work, model closures of the multiphase Reynolds-averaged Navier–Stokes (RANS) equations are developed for homogeneous, fully developed gas–particle flows. To date, the majority of RANS closures are based on extensions of single-phase turbulence models, which fail to capture complex two-phase flow dynamics across dilute and dense regimes, especially when two-way coupling between the phases is important. In the present study, particles settle under gravity in an unbounded viscous fluid. At sufficient mass loadings, interphase momentum exchange between the phases results in the spontaneous generation of particle clusters that sustain velocity fluctuations in the fluid. Data generated from Eulerian–Lagrangian simulations are used in a sparse regression method for model closure that ensures form invariance. Particular attention is paid to modelling the unclosed terms unique to the multiphase RANS equations (drag production, drag exchange, pressure strain and viscous dissipation). A minimal set of tensors is presented that serve as the basis for modelling. It is found that sparse regression identifies compact, algebraic models that are accurate across flow conditions and robust to sparse training data.

Turbulent mixing exerts a significant influence on many physical processes in the ocean. In a stably stratified Boussinesq fluid, this irreversible mixing describes the conversion of available potential energy (APE) to background potential energy (BPE). In some settings the APE framework is difficult to apply and approximate measures are used to estimate irreversible mixing. For example, numerical simulations of stratified turbulence often use triply periodic domains to increase computational efficiency. In this set-up, however, BPE is not uniquely defined and the method of Winters et al. (J. Fluid Mech., vol. 289, 1995, pp. 115–128) cannot be directly applied to calculate the APE. We propose a new technique to calculate APE in periodic domains with a mean stratification. By defining a control volume bounded by surfaces of constant buoyancy, we can construct an appropriate background buoyancy profile $b_\ast (z,t)$ and accurately quantify diapycnal mixing in such systems. This technique also permits the accurate calculation of a finite-amplitude local APE density in periodic domains. The evolution of APE is analysed in various turbulent stratified flow simulations. We show that the mean dissipation rate of buoyancy variance $\chi$ provides a good approximation to the mean diapycnal mixing rate, even in flows with significant variations in local stratification. When quantifying measures of mixing efficiency in transient flows, we find significant variation depending on whether laminar diffusion of a mean flow is included in the kinetic energy dissipation rate. We discuss how best to interpret these results in the context of quantifying diapycnal diffusivity in real oceanographic flows.

Direct numerical simulations have been performed for turbulent thermal convection between horizontal no-slip, permeable walls with a distance 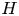$H$ and a constant temperature difference 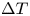$\Delta T$ at the Rayleigh number 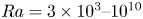$Ra=3\times 10^3\text {--}10^{10}$. On the no-slip wall surfaces $z=0$, 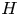$H$, the wall-normal (vertical) transpiration velocity is assumed to be proportional to the local pressure fluctuation, i.e. 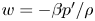$w=-\beta p'/\rho$, 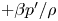$+\beta p'/\rho$ (Jiménez et al., J. Fluid Mech., vol. 442, 2001, pp. 89–117). Here 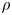$\rho$ is mass density, and the property of the permeable wall is given by the permeability parameter 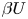$\beta U$ normalised with the buoyancy-induced terminal velocity 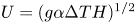$U=(g\alpha \Delta TH)^{1/2}$, where 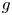$g$ and 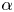$\alpha$ are acceleration due to gravity and volumetric thermal expansivity, respectively. The critical transition of heat transfer in convective turbulence has been found between the two 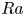$Ra$ regimes for fixed 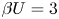$\beta U=3$ and fixed Prandtl number 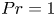$Pr=1$. In the subcritical regime at lower 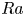$Ra$ the Nusselt number 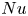$Nu$ scales with 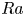$Ra$ as 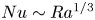$Nu\sim Ra^{1/3}$, as commonly observed in turbulent Rayleigh–Bénard convection. In the supercritical regime at higher 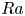$Ra$, on the other hand, the ultimate scaling 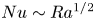$Nu\sim Ra^{1/2}$ is achieved, meaning that the wall-to-wall heat flux scales with 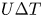$U\Delta T$ independent of the thermal diffusivity, although the heat transfer on the wall is dominated by thermal conduction. In the supercritical permeable case, large-scale motion is induced by buoyancy even in the vicinity of the wall, leading to significant transpiration velocity of the order of 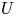$U$. The ultimate heat transfer is attributed to this large-scale significant fluid motion rather than to transition to turbulence in boundary-layer flow. In such ‘wall-bounded’ convective turbulence, a thermal conduction layer still exists on the wall, but there is no near-wall layer of large change in the vertical velocity, suggesting that the effect of the viscosity is negligible even in the near-wall region. The balance between the dominant advection and buoyancy terms in the vertical Boussinesq equation gives us the velocity scale of 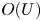$O(U)$ in the whole region, so that the total energy budget equation implies the Taylor dissipation law 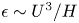$\epsilon \sim U^3/H$ and the ultimate scaling 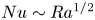$Nu\sim Ra^{1/2}$.

We found a multi-scale steady solution of the Boussinesq equations for Rayleigh–Bénard convection in a three-dimensional periodic domain between horizontal plates with a constant temperature difference. This was realised using a homotopy from the wall-to-wall optimal transport solution provided by Motoki et al. (J. Fluid Mech., vol. 851, 2018, R4). A connected steady solution, which is a consequence of bifurcation from a thermal conduction state at Rayleigh number $Ra\sim 10^{3}$, is tracked up to $Ra\sim 10^{7}$ using a Newton–Krylov iteration. The three-dimensional exact coherent thermal convection exhibits a scaling of $Nu\sim Ra^{0.31}$ (where $Nu$ is the Nusselt number) as well as multi-scale thermal plume and vortex structures, which are quite similar to those in turbulent Rayleigh–Bénard convection. The mean temperature profiles and the root-mean-square of the temperature and velocity fluctuations are in good agreement with those of the turbulent states. Furthermore, the energy spectrum follows Kolmogorov's $-5/3$ scaling law with a consistent prefactor, and the energy transfer to small scales with a nearly constant flux in the wavenumber space is in accordance with the turbulent energy transfer.

We consider the situation of a misalignment between the global temperature gradient and gravity in thermal convection. In such a case an effective horizontal buoyancy arises that will significantly influence the transport properties of heat, mass and momentum. It may also change the flow morphology in turbulent convection. In this paper, we present an experimental and numerical study, using Rayleigh–Bénard convection as a platform, to explore systematically the effect of horizontal buoyancy on heat transport in turbulent thermal convection. Experimentally, a condition of increasing horizontal Rayleigh number ($Ra_H$, which is the non-dimensional horizontal thermal driving strength) under fixed vertical Rayleigh number ($Ra_V$, the non-dimensional vertical driving strength) is achieved by tilting the convection cell and simultaneously increasing the imposed temperature difference. We find that, with increasing horizontal to vertical buoyancy ratio ($\varLambda = Ra_H/Ra_V$), the overall heat transport manifests a monotonic increase in vertical heat transport ($Nu_V$) as well as a monotonic increase in its horizontal component ($Nu_H$). However, the horizontal Nusselt number is found to be approximately one order of magnitude smaller than the vertical Nusselt for the parameter range explored. We also show that the non-zero $Nu_H$ results from the broken azimuthal symmetry of the system induced by the horizontal buoyancy. We find that the enhancement of vertical heat transport comes from the increased shear generated by the horizontal buoyancy at the boundary layer. The effect of Prandtl number ($Pr$) is also studied numerically. Finally, we extend the Grossmann–Lohse theory to the case with an effective horizontal buoyancy, the result of which is successful in predicting $Nu_V(Ra_V,\varLambda ,Pr)$.

A fully connected neural network (NN) is used to develop a subgrid-scale (SGS) model mapping the relation between the SGS stresses and filtered flow variables in a turbulent channel flow at $Re_\tau = 178$. A priori and a posteriori tests are performed to investigate its prediction performance. In a priori test, an NN-based SGS model with the input filtered strain rate or velocity gradient tensor at multiple points provides highest correlation coefficients between the predicted and true SGS stresses, and reasonably predicts the backscatter. However, this model provides unstable solution in a posteriori test, unless a special treatment such as backscatter clipping is used. On the other hand, an NN-based SGS model with the input filtered strain rate tensor at single point shows an excellent prediction capability for the mean velocity and Reynolds shear stress in a posteriori test, although it gives low correlation coefficients between the true and predicted SGS stresses in a priori test. This NN-based SGS model trained at $Re_\tau = 178$ is applied to a turbulent channel flow at $Re_\tau = 723$ using the same grid resolution in wall units, providing fairly good agreements of the solutions with the filtered direct numerical simulation (DNS) data. When the grid resolution in wall units is different from that of trained data, this NN-based SGS model does not perform well. This is overcome by training an NN with the datasets having two filters whose sizes are bigger and smaller than the grid size in large eddy simulation (LES). Finally, the limitations of NN-based LES to complex flow are discussed.

To design and optimize arrays of vertical-axis wind turbines (VAWTs) for maximal power density and minimal wake losses, a careful consideration of the inherently three-dimensional structure of the wakes of these turbines in real operating conditions is needed. Accordingly, a new volumetric particle-tracking velocimetry method was developed to measure three-dimensional flow fields around full-scale VAWTs in field conditions. Experiments were conducted at the Field Laboratory for Optimized Wind Energy (FLOWE) in Lancaster, CA, using six cameras and artificial snow as tracer particles. Velocity and vorticity measurements were obtained for a 2 kW turbine with five straight blades and a 1 kW turbine with three helical blades, each at two distinct tip-speed ratios and at Reynolds numbers based on the rotor diameter $D$ between $1.26 \times 10^{6}$ and $1.81 \times 10^{6}$. A tilted wake was observed to be induced by the helical-bladed turbine. By considering the dynamics of vortex lines shed from the rotating blades, the tilted wake was connected to the geometry of the helical blades. Furthermore, the effects of the tilted wake on a streamwise horseshoe vortex induced by the rotation of the turbine were quantified. Lastly, the implications of this dynamics for the recovery of the wake were examined. This study thus establishes a fluid-mechanical connection between the geometric features of a VAWT and the salient three-dimensional flow characteristics of its near-wake region, which can potentially inform both the design of turbines and the arrangement of turbines into highly efficient arrays.