Research Article
Stability of solitary wave solutions of simultaneous nonlinear Schrödinger equations
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 379-383
The crossfield current-driven ion-acoustic instability in a collisional plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 385-394
The shear Alfvén continuous spectrum of axisymmetric toroidal equilibria in the large aspect ratio limit
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 395-414
Fast magnetic field-line reconnexion in a compressible fluid. Part 2. Skewed field lines
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 415-443
Generalized expressions for momentum and energy losses of charged particle beams in non-Maxwellian multi-species plasmas and spherical symmetry
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 445-457
Evolution of nonlinear Alfvén waves propagating along the magnetic field in a collisionless plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 459-468
Growth rates of bending KdV solitons
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 469-484
Stochasticity in plasmas with electromagnetic waves
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 485-493
Nonlinear stability of doublets against axisymmetric resistive MHD modes
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 495-501
Electromagnetic cyclotron-loss-cone instability associated with weakly relativistic electrons
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 503-525
Lower-hybrid instability in current-carrying plasmas
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 527-537
Nonlinear interaction of spherical waves in a homogeneous isotropic plasma
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 539-550
Collisionless electrostatic interchange instabilities
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 551-564
Energy transfer in magnetized plasmas
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 565-573
Author Index to Volume 28
Index
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 575-577
Front matter
PLA volume 28 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service
Back matter
PLA volume 28 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. b1-b10
-
- Article
-
- You have access
- Export citation
- NASA ADS Abstract Service

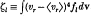 , which reflect the role of the non-Maxwellian tails. The familiar stopping power expression holding for Maxwellian targets is recovered as a particular case.
, which reflect the role of the non-Maxwellian tails. The familiar stopping power expression holding for Maxwellian targets is recovered as a particular case.