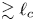JPP Letters
Contents
Letter
Weakly collisional steady state linear and nonlinear plasma waves
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 23 May 2025, E80
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Reduced modelling of scrape-off losses of runaway electrons during tokamak disruptions
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 3 / 2025
- Published online by Cambridge University Press:
- 19 May 2025, E78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Intermittent, reflection-driven, strong imbalanced MHD turbulence
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 2 / 2025
- Published online by Cambridge University Press:
- 22 April 2025, E57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Unusual electron temperature profile due to grain electrostatics in planetary nebula cored dusty plasma
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 1 / 2025
- Published online by Cambridge University Press:
- 12 March 2025, E41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Measurement of the properties of the dust acoustic wave in a magnetic field
- Part of:
-
- Journal:
- Journal of Plasma Physics / Volume 91 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 09 January 2025, E15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Effect of insulator end cap thickness on time-dependent Hartmann flow in a rotating mirror
-
- Journal:
- Journal of Plasma Physics / Volume 90 / Issue 6 / 2024
- Published online by Cambridge University Press:
- 20 December 2024, 175900603
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Optimised stellarators with a positive radial electric field
-
- Journal:
- Journal of Plasma Physics / Volume 90 / Issue 6 / 2024
- Published online by Cambridge University Press:
- 28 November 2024, 175900602
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Interplay of the magnetic and current density field topologies in axisymmetric devices for magnetic confinement fusion
-
- Journal:
- Journal of Plasma Physics / Volume 90 / Issue 6 / 2024
- Published online by Cambridge University Press:
- 12 November 2024, 175900601
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Reduction of electrostatic turbulence in a quasi-helically symmetric stellarator via critical gradient optimization
- Part of:
-
- Journal:
- Journal of Plasma Physics / Volume 90 / Issue 3 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, 175900301
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Direct, simple and efficient computation of all components of the virtual-casing magnetic field in axisymmetric geometries with Kapur–Rokhlin quadrature
-
- Journal:
- Journal of Plasma Physics / Volume 90 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 06 May 2024, 175900202
Hybrid electrostatic waves in linearized gravity
-
- Journal:
- Journal of Plasma Physics / Volume 90 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 29 April 2024, 175900201
Transformation of a plasma boundary curvature into electrical impulses moving along a plasma surface
-
- Journal:
- Journal of Plasma Physics / Volume 90 / Issue 1 / 2024
- Published online by Cambridge University Press:
- 08 February 2024, 905900111
Deciphering the physical basis of the intermediate-scale instability
-
- Journal:
- Journal of Plasma Physics / Volume 89 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 12 December 2023, 175890603
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service
Hall magnetohydrodynamics in a relativistically strong mean magnetic field
-
- Journal:
- Journal of Plasma Physics / Volume 89 / Issue 6 / 2023
- Published online by Cambridge University Press:
- 12 December 2023, 175890602
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
On the analytical description of the nonlinear stage of the Weibel instability in collisionless anisotropic plasma
-
- Journal:
- Journal of Plasma Physics / Volume 89 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 08 November 2023, 175890601
Particle transport through localized interactions with sharp magnetic field bends in MHD turbulence
- Part of:
-
- Journal:
- Journal of Plasma Physics / Volume 89 / Issue 5 / 2023
- Published online by Cambridge University Press:
- 14 September 2023, 175890501
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Observations of dust fragmentations in the Experimental Advanced Superconducting Tokamak
-
- Journal:
- Journal of Plasma Physics / Volume 89 / Issue 2 / 2023
- Published online by Cambridge University Press:
- 21 April 2023, 175890202
-
- Article
-
- You have access
- HTML
- Export citation
- NASA ADS Abstract Service
Validation of magnetized gas-jet experiments to investigate the effects of an external magnetic field on laser-plasma instabilities
-
- Journal:
- Journal of Plasma Physics / Volume 89 / Issue 2 / 2023
- Published online by Cambridge University Press:
- 13 March 2023, 175890201
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
Hosking integral in non-helical Hall cascade
-
- Journal:
- Journal of Plasma Physics / Volume 89 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 20 February 2023, 175890101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service
A single-field-period quasi-isodynamic stellarator
-
- Journal:
- Journal of Plasma Physics / Volume 88 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 28 September 2022, 175880504
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- NASA ADS Abstract Service