Consequences of fluctuating microscopic conductivity in mean-field electrodynamics of turbulent fluids are formulated and discussed. If the conductivity fluctuations are assumed to be uncorrelated with the velocity fluctuations then only the turbulence-originated magnetic diffusivity of the fluid is reduced and the decay time of a large-scale magnetic field or the cycle times of oscillating turbulent dynamo models are increased. If, however, the fluctuations of conductivity and flow in a certain well-defined direction are correlated, an additional diamagnetic pumping effect results, transporting the magnetic field in the opposite direction to the diffusivity flux vector $\langle \unicode[STIX]{x1D702}^{\prime }\boldsymbol{u}^{\prime }\rangle$. In the presence of global rotation, even for homogeneous turbulence fields, an alpha effect appears. If the characteristic values of the outer core of the Earth or the solar convection zone are applied, the dynamo number of the new alpha effect does not reach supercritical values to operate as an $\unicode[STIX]{x1D6FC}^{2}$-dynamo but oscillating $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FA}$-dynamos with differential rotation are not excluded.

Numerical simulations of Alfvén modes driven by energetic particles are performed with the gyrokinetic (GK) global particle-in-cell code ORB5. A reversed shear equilibrium magnetic field is adopted. A simplified configuration with circular flux surfaces and large aspect ratio is considered. The nonlinear saturation of beta-induced Alfvén eigenmodes (BAE) is investigated. The roles of the wave–particle nonlinearity of the different species, i.e. thermal ions, electrons and energetic ions are described, in particular for their role in the saturation of the BAE and the generation of zonal flows. The nonlinear redistribution of the electron population is found to be important in increasing the BAE saturation level and the zonal flow amplitude.

We derive a sufficient condition for the linear stability of plasma equilibria with incompressible flow parallel to the magnetic field, $\boldsymbol{B}$, constant mass density and anisotropic pressure such that the quantity $\unicode[STIX]{x1D70E}_{d}=\unicode[STIX]{x1D707}_{0}(P_{\Vert }-P_{\bot })/B^{2}$, where $P_{\Vert }$ ($P_{\bot }$) is the pressure tensor element parallel (perpendicular) to $\boldsymbol{B}$, remains constant. This condition is applicable to any steady state without geometrical restriction. The condition, generalising the respective condition for magnetohydrodynamic equilibria with isotropic pressure and constant density derived in Throumoulopoulos & Tasso (Phys. Plasmas, vol. 14, 2007, 122104), involves physically interpretable terms related to the magnetic shear, the flow shear and the variation of total pressure perpendicular to the magnetic surfaces. On the basis of this condition we prove that, if a given equilibrium is linearly stable, then the ones resulting from the application of Bogoyavlenskij symmetry transformations are linearly stable too, provided that a parameter involved in those transformations is positive. In addition, we examine the impact of pressure anisotropy, flow and torsion of a helical magnetic axis, for a specific class of analytic equilibria. In this case, we find that the pressure anisotropy and the flow may have either stabilising or destabilising effects. Also, helical configurations with small torsion and large pitch seem to have more favourable stability properties.

The turbulence-induced quasi-linear particle flux of a highly charged, collisional impurity species is calculated from the electrostatic gyrokinetic equation including collisions with the bulk ions and the impurities themselves. The equation is solved by an expansion in powers of the impurity charge number $Z$. In this formalism, the collision operator only affects the impurity flux through the dynamics of the impurities in the direction parallel to the magnetic field. At reactor-relevant collisionality, the parallel dynamics is dominated by the parallel electric field, and collisions have a minor effect on the turbulent particle flux of highly charged, collisional impurities.

The island divertor topology of the Wendelstein 7-X (W7-X) scrape-off-layer exhibits regions of highly varying connection length. Here, we present drift-plane simulations of seeded filaments in regions of sharp transitions in parallel connection length – a parameter which dictates the propagation regime for plasma blobs. It is determined that a transition in parallel connection length alters the trajectory of filaments; filaments which enter regions of lower connection length are decelerated, and vice versa. It is also determined that if the lobes of a potential dipole created by diamagnetic drifts within the filament exist in two regions of distinct parallel connection length, the filament is then steered towards the region of higher connection length. The extreme case of a narrow region of varying connection length can also alter the trajectory of a filament, depending on the extent of this region. Finally, simulations mimicking the view from the W7-X gas puff imaging (GPI) diagnostic view plane are presented. It is determined that filaments in the view of the W7-X GPI diagnostic exhibit a predominantly poloidal propagation due to the radial electric field, since the radial velocity is relatively small.

The creation of well-thermalized, hot and dense plasmas is attractive for warm dense matter studies. We investigate collisionally induced energy absorption of an ultraintense and ultrashort laser pulse in a solid copper target using particle-in-cell simulations. We find that, upon irradiation by a $2\times 10^{20}~\text{W}\,\text{cm}^{-2}$ intensity, 60 fs duration, circularly polarized laser pulse, the electrons in the collisional simulation rapidly reach a well-thermalized distribution with ${\sim}3.5~\text{keV}$ temperature, while in the collisionless simulation the absorption is several orders of magnitude weaker. Circular polarization inhibits the generation of suprathermal electrons, while ensuring efficient bulk heating through inverse bremsstrahlung, a mechanism usually overlooked at relativistic laser intensity. An additional simulation, taking account of both collisional and field ionization, yields similar results: the bulk electrons are heated to ${\sim}2.5~\text{keV}$, but with a somewhat lower degree of thermalization than in the pre-set, fixed-ionization case. The collisional absorption mechanism is found to be robust against variations in the laser parameters. At fixed laser pulse energy, increasing the pulse duration rather than the intensity leads to a higher electron temperature.

Linear gyrokinetic simulations of magnetically confined electron–positron plasmas are performed for the first time in the geometry and parameter regimes likely to be relevant for upcoming laboratory experiments. In such plasmas, the density will be sufficiently small as to render the plasma effectively collisionless. The magnetic field will be very large, meaning that the Debye length will exceed the gyroradius by a few orders of magnitude. We show the results of linear simulations in flux tubes close to the current carrying ring and also in the bulk of the plasma, demonstrating the existence of entropy modes and interchange modes in pair plasmas. We study linear stability and show that in the relevant configurations, almost complete linear stability is attainable in large swathes of parameter space.

Following up on earlier work which demonstrated an improved numerical stellarator coil design optimization performance by the use of stochastic optimization (Lobsien et al., Nucl. Fusion, vol. 58 (10), 2018, 106013), it is demonstrated here that significant further improvements can be made – lower field errors and improved robustness – for a Wendelstein 7-X test case. This is done by increasing the sample size and applying fully three-dimensional perturbations, but most importantly, by changing the design sequence in which the optimization targets are applied: optimization for field error is conducted first, with coil shape penalties only added to the objective function at a later step in the design process. A robust, feasible coil configuration with a local maximum field error of 3.66 % and an average field error of 0.95 % is achieved here, as compared to a maximum local field error of 6.08 % and average field error of 1.56 % found in our earlier work. These new results are compared to those found without stochastic optimization using the FOCUS and ONSET suites. The relationship between local minima in the optimization space and coil shape penalties is also discussed.

Accelerated statistical computation of collisionless fusion alpha particle losses in stellarator configurations is presented based on direct guiding-centre orbit tracing. The approach relies on the combination of recently developed symplectic integrators in canonicalized magnetic flux coordinates and early classification into regular and chaotic orbit types. Only chaotic orbits have to be traced up to the end, as their behaviour is unpredictable. An implementation of this technique is provided in the code SIMPLE (symplectic integration methods for particle loss estimation, Albert et al., 2020b, doi:10.5281/zenodo.3666820). Reliable results were obtained for an ensemble of 1000 orbits in a quasi-isodynamic, a quasi-helical and a quasi-axisymmetric configuration. Overall, a computational speed up of approximately one order of magnitude is achieved compared to direct integration via adaptive Runge–Kutta methods. This reduces run times to the range of typical magnetic equilibrium computations and makes direct alpha particle loss computation adequate for use within a stellarator optimization loop.

The problem of plasma expansion into a vacuum is revisited with the addition of a finite boundary condition; an electrically insulated surface. As plasma expands towards a charge-accumulating surface, the leading electron cloud charges the surface negatively, which in turn repels electrons and attracts ions. This plasma–surface interaction is shown to result in a feedback process which accelerates the plasma expansion. In addition, we examine the decrease in (negative) surface potential and associated near-surface electron density. To investigate this plasma coupling with an electrically floating surface, we develop an analytic model including four neighbouring plasma regions: (i) undisturbed plasma, (ii) quasi-neutral self-similar expansion, (iii) ion front boundary layer and (iv) electron cloud. A key innovation in our approach is a self-contained analytic approximation of the ion front boundary layer, providing a spatially continuous electric field model for the early phase of bounded plasma expansion.

The concept of the available energy of a collisionless plasma is discussed in the context of magnetic confinement. The available energy quantifies how much of the plasma energy can be converted into fluctuations (including nonlinear ones) and is thus a measure of plasma stability, which can be used to derive linear and nonlinear stability criteria without solving an eigenvalue problem. In a magnetically confined plasma, the available energy is determined by the density and temperature profiles as well as the magnetic geometry. It also depends on what constraints limit the possible forms of plasma motion, such as the conservation of adiabatic invariants and the requirement that the transport be ambipolar. A general method based on Lagrange multipliers is devised to incorporate such constraints in the calculation of the available energy, and several particular cases are discussed for which it can be calculated explicitly. In particular, it is shown that it is impossible to confine a plasma in a Maxwellian ground state relative to perturbations with frequencies exceeding the ion bounce frequency.

In recent years, several optimal dynamos have been discovered. They minimize the magnetic energy dissipation or, equivalently, maximize the growth rate at a fixed magnetic Reynolds number. In the optimal dynamo of Willis (Phys. Rev. Lett., vol. 109, 2012, 251101), we find mean-field dynamo action for planar averages. One component of the magnetic field grows exponentially while the other decays in an oscillatory fashion near onset. This behaviour is different from that of an 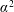$\unicode[STIX]{x1D6FC}^{2}$ dynamo, where the two non-vanishing components of the planar averages are coupled and have the same growth rate. For the Willis dynamo, we find that the mean field is excited by a negative turbulent magnetic diffusivity, which has a non-uniform spatial profile near onset. The temporal oscillations in the decaying component are caused by the corresponding component of the diffusivity tensor being complex when the mean field is decaying and, in this way, time dependent. The growing mean field can be modelled by a negative magnetic diffusivity combined with a positive magnetic hyperdiffusivity. In two other classes of optimal dynamos of Chen et al. (J. Fluid Mech., vol. 783, 2015, pp. 23–45), we find, to some extent, similar mean-field dynamo actions. When the magnetic boundary conditions are mixed, the two components of the planar averaged field grow at different rates when the dynamo is 15 % supercritical. When the mean magnetic field satisfies homogeneous boundary conditions (where the magnetic field is tangential to the boundary), mean-field dynamo action is found for one-dimensional averages, but not for planar averages. Despite having different spatial profiles, both dynamos show negative turbulent magnetic diffusivities. Our finding suggests that negative turbulent magnetic diffusivities may support a broader class of dynamos than previously thought, including these three optimal dynamos.

Plasma terminating disruptions in tokamaks may result in relativistic runaway electron beams with potentially serious consequences for future devices with large plasma currents. In this paper, we investigate the effect of plasma elongation on the coupled dynamics of runaway generation and resistive diffusion of the electric field. We find that elongated plasmas are less likely to produce large runaway currents, partly due to the lower induced electric fields associated with larger plasmas, and partly due to direct shaping effects, which mainly lead to a reduction in the runaway avalanche gain.

Using particle-in-cell simulations, we demonstrate an improvement of the target-normal-sheath acceleration (TNSA) of protons in non-periodically nanostructured targets with micron-scale thickness. Compared to standard flat foils, an increase in the proton cutoff energy by up to a factor of two is observed in foils coated with nanocones or perforated with nanoholes. The latter nano-perforated foils yield the highest enhancement, which we show to be robust over a broad range of foil thicknesses and hole diameters. The improvement of TNSA performance results from more efficient hot-electron generation, caused by a more complex laser–electron interaction geometry and increased effective interaction area and duration. We show that TNSA is optimized for a nanohole distribution of relatively low areal density and that is not required to be periodic, thus relaxing the manufacturing constraints.

A non-parametric Gaussian process regression model is developed in the three-dimensional equilibrium reconstruction code V3FIT. A Gaussian process is a normal distribution of functions that is uniquely defined by specifying a mean function and covariance kernel function. Gaussian process regression assumes that an unknown profile belongs to a particular Gaussian process and uses Bayesian analysis to select the function the give the best fit to measured data. The implementation in V3FIT uses a hybrid representation where Gaussian processes are used to infer some of the equilibrium profiles and standard parametric techniques are used to infer the remaining profiles. The implementation of the Gaussian process is tested using both synthetic data and experimental data from multiple machines.

We present a detailed guide to advanced collisionless fluid models that incorporate kinetic effects into the fluid framework, and that are much closer to the collisionless kinetic description than traditional magnetohydrodynamics. Such fluid models are directly applicable to modelling the turbulent evolution of a vast array of astrophysical plasmas, such as the solar corona and the solar wind, the interstellar medium, as well as accretion disks and galaxy clusters. The text can be viewed as a detailed guide to Landau fluid models and it is divided into two parts. Part 1 is dedicated to fluid models that are obtained by closing the fluid hierarchy with simple (non-Landau fluid) closures. Part 2 is dedicated to Landau fluid closures. Here in Part 1, we discuss the fluid model of Chew–Goldberger–Low (CGL) in great detail, together with fluid models that contain dispersive effects introduced by the Hall term and by the finite Larmor radius corrections to the pressure tensor. We consider dispersive effects introduced by the non-gyrotropic heat flux vectors. We investigate the parallel and oblique firehose instability, and show that the non-gyrotropic heat flux strongly influences the maximum growth rate of these instabilities. Furthermore, we discuss fluid models that contain evolution equations for the gyrotropic heat flux fluctuations and that are closed at the fourth-moment level by prescribing a specific form for the distribution function. For the bi-Maxwellian distribution, such a closure is known as the ‘normal’ closure. We also discuss a fluid closure for the bi-kappa distribution. Finally, by considering one-dimensional Maxwellian fluid closures at higher-order moments, we show that such fluid models are always unstable. The last possible non Landau fluid closure is therefore the ‘normal’ closure, and beyond the fourth-order moment, Landau fluid closures are required.

In Part 2 of our guide to collisionless fluid models, we concentrate on Landau fluid closures. These closures were pioneered by Hammett and Perkins and allow for the rigorous incorporation of collisionless Landau damping into a fluid framework. It is Landau damping that sharply separates traditional fluid models and collisionless kinetic theory, and is the main reason why the usual fluid models do not converge to the kinetic description, even in the long-wavelength low-frequency limit. We start with a brief introduction to kinetic theory, where we discuss in detail the plasma dispersion function $Z(\unicode[STIX]{x1D701})$, and the associated plasma response function $R(\unicode[STIX]{x1D701})=1+\unicode[STIX]{x1D701}Z(\unicode[STIX]{x1D701})=-Z^{\prime }(\unicode[STIX]{x1D701})/2$. We then consider a one-dimensional (1-D) (electrostatic) geometry and make a significant effort to map all possible Landau fluid closures that can be constructed at the fourth-order moment level. These closures for parallel moments have general validity from the largest astrophysical scales down to the Debye length, and we verify their validity by considering examples of the (proton and electron) Landau damping of the ion-acoustic mode, and the electron Landau damping of the Langmuir mode. We proceed by considering 1-D closures at higher-order moments than the fourth order, and as was concluded in Part 1, this is not possible without Landau fluid closures. We show that it is possible to reproduce linear Landau damping in the fluid framework to any desired precision, thus showing the convergence of the fluid and collisionless kinetic descriptions. We then consider a 3-D (electromagnetic) geometry in the gyrotropic (long-wavelength low-frequency) limit and map all closures that are available at the fourth-order moment level. In appendix A, we provide comprehensive tables with Padé approximants of $R(\unicode[STIX]{x1D701})$ up to the eighth-pole order, with many given in an analytic form.

Integrated modelling of electron runaway requires computationally expensive kinetic models that are self-consistently coupled to the evolution of the background plasma parameters. The computational expense can be reduced by using parameterized runaway generation rates rather than solving the full kinetic problem. However, currently available generation rates neglect several important effects; in particular, they are not valid in the presence of partially ionized impurities. In this work, we construct a multilayer neural network for the Dreicer runaway generation rate which is trained on data obtained from kinetic simulations performed for a wide range of plasma parameters and impurities. The neural network accurately reproduces the Dreicer runaway generation rate obtained by the kinetic solver. By implementing it in a fluid runaway-electron modelling tool, we show that the improved generation rates lead to significant differences in the self-consistent runaway dynamics as compared to the results using the previously available formulas for the runaway generation rate.

The condition of omnigenity is investigated, and applied to the near-axis expansion of Garren & Boozer (Phys. Fluids B, vol. 3 (10), 1991a, pp. 2805–2821). Due in part to the particular analyticity requirements of the near-axis expansion, we find that, excluding quasi-symmetric solutions, only one type of omnigenity, namely quasi-isodynamicity, can be satisfied at first order in the distance from the magnetic axis. Our construction provides a parameterization of the space of such solutions, and the cylindrical reformulation and numerical method of Landreman & Sengupta (J. Plasma Phys., vol. 84 (6), 2018, 905840616); Landreman et al. (J. Plasma Phys., vol. 85 (1), 2019, 905850103), enables their efficient numerical construction.

Dipole and stellarator geometries are capable of confining plasmas of arbitrary neutrality, ranging from pure electron plasmas through to quasineutral. The diocotron mode is known to be important in non-neutral plasmas and has been widely studied. However, drift mode dynamics, dominating quasineutral plasmas, has received very little by way of attention in the non-neutral context. Here, we show that non-neutral plasmas can be unstable respect to both density-gradient- and temperature-gradient-driven instabilities. A local shearless slab limit is considered for simplicity. A key feature of non-neutral plasmas is the development of strong electric fields, in this local limit of straight field line geometry, the effect of the corresponding $\boldsymbol{E}\times \boldsymbol{B}$ drift is limited to the Doppler shift of the complex frequency $\unicode[STIX]{x1D714}\rightarrow \unicode[STIX]{x1D714}-\unicode[STIX]{x1D714}_{E}$. However, the breaking of the quasineutrality condition still leads to interesting dynamics in non-neutral plasmas. In this paper we address the behaviour of a number of gyrokinetic modes in electron–ion and electron–positron plasmas with arbitrary degree of neutrality.