Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Herzog, Ivo
1992.
Modules with few types.
Journal of Algebra,
Vol. 149,
Issue. 2,
p.
358.
Прест, М
Prest, M
Пунинская, Вера Александровна
and
Puninskaya, Vera Aleksandrovna
1999.
Модули с малым числом типов над коммутативным прюферовым кольцом.
Успехи математических наук,
Vol. 54,
Issue. 3,
p.
149.
Puninskaya, V. A.
2002.
Vaught's Conjecture.
Journal of Mathematical Sciences,
Vol. 109,
Issue. 3,
p.
1649.

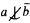 .
. 