No CrossRef data available.
Article contents
On the transversal hypothesis and the weak kurepa hypothesis
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper the theory of the core model K is applied to study certain combinatorial principles. These principles concern the existence of families of almost disjoint functions. The first, the transversal hypothesis, is defined as follows.
Definition. The transversal hypothesis for κ, T(κ), is the following assertion:
There is a sequence 〈fν: ν < κ+〉 such that
(a) fν: κ → κ regressively for ν < κ+, and
(b) if ν < ξ < κ+, then there is γ < κ such that fν(α) ≠ fξ(α) whenever γ < α < κ.
T(κ) is a simple consequence of the Kurepa hypothesis for κ, i.e. the assertion, KH(κ), that there is a family F ⊂ P(κ) such that 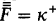 and card({X ∩ α: X ϵ F}) ≤ α for ω < α < κ.
and card({X ∩ α: X ϵ F}) ≤ α for ω < α < κ.
The second principle to be studied, the weak Kurepa hypothesis, is a statement of strength intermediate between the Kurepa and transversal hypotheses.
Definition. The weak Kurepa hypothesis for κ, wKH(κ), is the following assertion:
There is a sequence 〈bν: ν < κ+〉 such that
(a) bν ⊂ κ for ν < κ+, and
(b) for each limit λ < κ there is Fλ: {bν ∩ λ: ν < κ+} → λ such that setting fν(λ) = Fλ(bν ∩ λ) for ν < κ+ and limit λ < κ, if ν < ξ < κ+ there is γ < κ such that fν(λ) ≠ fξ(λ) whenever γ < λ < κ and λ is a limit.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1988

