The consistency of classical set theory relative to a set theory with intu1tionistic logic

Extract

Let ZF be the usual Zermelo-Fraenkel set theory formulated without identity, and with the collection axiom scheme. Let ZF⁻-extensionality be obtained from ZF by using intuitionistic logic instead of classical logic, and dropping the axiom of extensionality. We give a syntactic transformation of ZF into ZF⁻-extensionality.

Let CPC, HPC respectively be classical, intuitionistic predicate calculus without identity, whose only homological symbol is ∈. We use the ~ ~-translation, a basic tool in the metatheory of intuitionistic systems, which is defined by

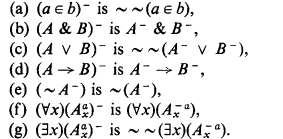
The two fundamental lemmas about this ~ ~ -translation we will use are

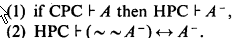
For proofs, see Kleene [3, Lemma 43a, Theorem 60d].

This - would provide the desired syntactic transformation at least for ZF into ZF⁻ with extensionality, if A⁻ were provable in ZF⁻ for each axiom A of ZF. Unfortunately, the ~ ~-translations of extensionality and power set appear not to be provable in ZF⁻. We therefore form an auxiliary classical theory S which has no extensionality and has a weakened power set axiom, and show in §2 that the ~ ~-translation of each axiom of Sis provable in ZF⁻-extensionality. §1 is devoted to the translation of ZF in S.