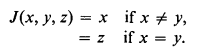By an elementary condition in the variablesx1, …, xn, we mean a conjunction of the form x1 ≤ i < j ≤ naij where each aij is one of the formulas xi = xj or xi ≠ xj. (We should add that the formula x1 = x1 should be regarded as an elementary condition in the one variable x1.)

Clearly, according to this definition, some elementary conditions are inconsistent, some are consistent. For instance (in the variables x1, x2, x3) the conjunction x1 = x2 & x1 = x3 & x2 ≠ x3 is inconsistent.

By an elementary combinatorial function (ex. function) we mean any function which can be given a definition of the form

where E1(x1, …, xn), …, Ek(x1, …, xn) is an enumeration of all consistent elementary conditions in x1, …, xn, and all the numbers d1, …, dk are among 1, …, n.

Examples. (1) The identity function is the only 1-ary e.c. function.

(2) A useful 3-ary e.c. function will be called J. The definition is

Nonstandard analysis was developed in [1] within a logic which has a language with finite types. In [2] and [3] the logic is first order and the language is that of set theory. The set theoretical approach can be described in the following setting.

Let be a relational structure (A, ∈) where A is a nonempty set and ∈ is a restriction of the elementhood relation of set theory.

Let Ext be the wf (∀x)[(∃w)[w ∈ x] → [(∀y)(∀z) [z ∈ x ↔ z ∈ y] → x = y]]. Call a fragment of set theory if ⊧ Ext. By forming a nontrivial ultrapower of one obtains a structure which, after canonically embedding in , becomes a proper elementary extension of .

Let j embed canonically in . Let be the substructure (B′, ∈′) of where B′ is the ∈′-closure of j(A) in B. That is, B′ is the smallest subset of B containing j(A) such that if b ∈ B, b′ ∈ B′ and ⊧ b ∈ b′ then b ∈ B′.

Definition 1. For a set S and a cardinal κ,

In particular, 2ω denotes the power set of the natural numbers and not the cardinal 2ℵ0. We regard 2ω as a topological space with the usual product topology.

Definition 2. A set S ⊆ 2ω is Ramsey if there is an M ∈ [ω]ω such that either [M]ω ⊆ S or else [M]ω ⊆ 2ω − S.

Erdös and Rado [3, Example 1, p. 434] showed that not every S ⊆ 2ω is Ramsey. In view of the nonconstructive character of the counterexample, one might expect (as Dana Scott has suggested) that all sufficiently definable sets are Ramsey. In fact, our main result (Theorem 2) is that all Borei sets are Ramsey. Soare [10] has applied this result to some problems in recursion theory.

The first positive result on Scott's problem was Ramsey's theorem [8, Theorem A]. The next advance was Nash-Williams' generalization of Ramsey's theorem (Corollary 2), which can be interpreted as saying: If S1 and S2 are disjoint open subsets of 2ω, there is an M ∈ [ω]ω such that either [M]ω ⋂ S1 = ∅ or [M]ω ∩ S2 = ⊆. (This is halfway between “clopen sets are Ramsey” and “open sets are Ramsey.”) Then Galvin [4] stated a generalization of Nash-Williams' theorem (Corollary 1) which says, in effect, that open sets are Ramsey; this was discovered independently by Andrzej Ehrenfeucht, Paul Cohen, and probably many others, but no proof has been published.

A recursively enumerable (r.e.) set is mitotic if it is the disjoint union of two r.e. sets both of the same degree of unsolvability. A. H. Lachlan has shown in [3] that there exists a nonmitotic r.e. set. In this paper we make an initial investigation into the class of mitotic sets.

The following results are proved, (i) An r.e. set is mitotic if and only if it is auto-reducible, (ii) There is a nonmitotic r.e. set of degree 0′, (iii) If d is an arbitrary non-recursive r.e. degree then there exists a nonmitotic r.e. set of degree ≤d. (iv) There exists a maximal set which is mitotic and a maximal set which is nonmitotic.

Albert R. Meyer had independently proved (ii) and (iii) for nonautoreducible sets before (i) was known.

The purpose of this note is to give a short proof of a conjecture of Feiner that every countable Boolean algebra has an ordered basis that is a lexicographic sum of well-ordered sets over the ordered set η of all rational numbers. Actually, we prove a slightly more precise fact, which is formulated below as Theorem 3. An earlier proof of Feiner's conjecture was obtained by David Cossack (unpublished), using a different method.

Our proof will use the following property of Cantor's dyadic discontinuum D.

In [4], I introduced a quasi-Boolean algebra, and showed that in a formal system of simple type theory, from which the cut rule is omitted, wffs form a quasi-Boolean algebra, and that the cut-elimination theorem can be formulated in algebraic language. In this paper we use the result of [4] to prove the cut-elimination theorem in simple type theory. The theorem was proved by M. Takahashi [2] in 1967 by using the concept of Schütte's semivaluation. We use maximal ideals of a quasi-Boolean algebra instead of semivaluations.

The logical system we are concerned with is a modification of Schütte's formal system of simple type theory in [1] into Gentzen style.

Inductive definition of types.

0 and 1 are types.

If τ1, …, τn are types, then (τ1, …, τn) is a type.

Basic symbols.

a1τ, a2τ, … for free variables of type τ.

x1τ, x2τ, … for bound variables of type τ.

An arbitrary number of constants of certain types.

An arbitrary number of function symbols with certain argument places.

This paper contains some observations on models for A2-second-order arithmetics. It arose from unsuccessful attempts to prove the Conjecture 1 (see at the end of the paper). Two partial solutions are given in this paper. We also give a sketch of a new proof of a classical result of descriptive set-theory referred to in [3]. Unless otherwise specified the word “model” means “ω-model for second-order arithmetics with the axiom scheme of choice,” i.e., “ω-model of A2” in the terminology of [3]. We say that a model M1 is shorter than M2 iff there is in M2 a relation A which is a well-ordering in M2 such that every relation B which is a well-ordering in M1 is similar to an initial segment of A. We denote by M0 the principal model of A2, i.e., a model which has only standard integers and contains all sets of integers.

In this paper I shall argue that the presumption of infinitude may be excised from the area of mathematics known as natural number theory with no substantial loss. Except for a few concluding remarks, I shall restrict my concern in here arguing the thesis to the business of constructing and developing a first-order axiomatic system for arithmetic (called ‘FA’ for finite arithmetic) that contains no theorem to the effect that there are infinitely many numbers.

The paper will consist of five parts. Part I characterizes the underlying logic of FA. In part II ordering of natural numbers is developed from a restricted set of axioms, induction schemata are proved and a way of expressing finitude presented. A full set of axioms are used in part III to prove working theorems on comparison of size. In part IV an ordinal expression is defined and characteristic theorems proved. Theorems for addition and multiplication are derived in part V from definitions in terms of the ordinal expression of part IV. The crucial final constructions of part V present a new method of replacing recursive characterizations by strict definitions.

In view of our resolution not to assume that there are infinitely many numbers, we shall have to deal with the situation where singular arithmetic terms of FA may fail to refer. For I know of no acceptable and systematic way of avoiding such situations. As a further result, singular-term instances of universal generalizations of FA are not to be inferred directly from the generalizations themselves. Nevertheless, (i) (x)(y)(x + y = y + x), for example, and all its instances are provable in FA.

The jump a′ of a degree a is defined to be the largest degree recursively enumerable in a in the upper semilattice of degrees of unsolvability. We examine below some of the ways in which the jump operation is related to the partial ordering of the degrees. Fried berg [3] showed that the equation a = x′ is solvable if and only if a ≥ 0′. Sacks [13] showed that we can find a solution of a = x′ which is ≤ 0′ (and in fact is r.e.) if and only if a ≥ 0′ and is r.e. in 0′. Spector [16] constructed a minimal degree and Sacks [13] constructed one ≤ 0′. So far the only result concerning the relationship between minimal degrees and the jump operator is one due to Yates [17] who showed that there is a minimal predecessor for each non-recursive r.e. degree, and hence that there is a minimal degree with jump 0′. In §1, we obtain an analogue of Friedberg's theorem by constructing a minimal degree solution for a = x′ whenever a ≥ 0′. We incorporate Friedberg5s original number-theoretic device with a complicated sequence of approximations to the nest of trees necessary for the construction of a minimal degree. The proof of Theorem 1 is a revision of an earlier, shorter presentation, and incorporates many additions and modifications suggested by R. Epstein. In §2, we show that any hope for a result analogous to that of Sacks on the jumps of r.e. degrees cannot be fulfilled since 0″ is not the jump of any minimal degree below 0′. We use a characterization of the degrees below 0′ with jump 0″ similar to that found for r.e. degrees with jump 0′ by R. W. Robinson [12]. Finally, in §3, we give a proof that every degree a ≤ 0′ with a′ = 0″ has a minimal predecessor. Yates [17] has already shown that every nonzero r.e. degree has a minimal predecessor, but that there is a nonzero degree ≤ 0′ with no minimal predecessor (see [18]; or for the original unrelativized result see [10] or [4]).

With reservations, one can think of abstract algebra as the study of what consequences can be drawn from the axioms associated with certain concrete algebraic structures. Two important examples of such concrete algebraic structures are the integers and the rational numbers. The integers and the rational numbers have two properties which are not in general mirrored in the abstract axiom systems associated with them. That is, the integers and the rational numbers both have effectively computable metrics and their algebraic operations are effectively computable. The study of abstract algebraic systems which possess effectively computable algebraic operations has produced many interesting results. One can think of a computable algebraic structure as one whose elements have been labeled by the set of positive integers and whose operations are effectively computable. The formal definition of computable local integral domain will be given in §3. Some specific computable structures which have been studied are the integers, the rational numbers, and the rational numbers with p-adic valuation. Computable structures were studied in general by Rabin [12]. This paper concerns computable local integral domains as exemplified by the local integral domain Zp. Zp is the localization of the integers with respect to the maximal prime ideal generated by the positive prime p. We should note that the concept of local integral domain is not first order.

Let the ordered pair (Q, M) stand for a local ring, where Q is the local ring and M is the unique maximal prime ideal of Q. Since most of my results are proving the existence of certain effective procedures, the assumption that Q has a principal maximal ideal M (rather than M has n generators) greatly simplifies many of the proofs.

Combinations of capital letters (e.g., G, EVEN) will be used as names of formulas of Peano arithmetic, x, y, z will be variables. Let be a model for Peano arithmetic. The names of formulas with a bar (e.g., G−, EVEN−(x)) will denote the relations defined by the formulas in . The elements of are called numbers.

By a finite sequence of numbers 〈a0, …, an〉 we mean a number . Note that n Pi's and ai's can be nonstandard elements and therefore “finite,” and all concepts which will use it are not absolute but relative to .

If a and b are degrees of unsolvability, a is called (as in [1]) a minimal cover of b if b < a and no degree c satisfies b < c < a. A degree a is called a minimal cover if it is a minimal cover of some degree b. We show in ZF set theory that there is a degree d such that every degree a ≥ d is a minimal cover. In [1] it was remarked that this result follows via a lemma of D. A. Martin [4] from the determinacy of a certain Σ50 Gale-Stewart game (which in turn follows [5] from the existence of a measurable cardinal). The argument here is parallel to that of [1], but the essential new ingredient is the result of Paris [6] that Σ50 determinacy can be proved in ZF. Also it is necessary to replace the Σ50 game of [1] by a related Σ40 game and to use the method, rather than just the statement, of Martin's lemma.

Theorem. There is a degreedsuch that every degreea ≥ dis a minimal cover.

Proof. In a (Gale–Stewart) game on 2ω, players I and II construct a set of integers A as follows: At the nth stage, player I determines whether n ϵ A if n is even and player II if n is odd. Thus player I controls A0 and player II controls A1 where Ai = {n: 2n + i ϵ A}. Let Aij denote (Ai)j and let M (A, B) mean that the degree of A is a minimal cover of that of B. Consider now the particular game in which player I wins iff M(A, A00) holds.

Let U be a consistent axiomatic theory containing Robinson's Q [TMRUT, p. 51]. In order for the results below to be of interest, U must be powerful enough to carry out certain arguments involving versions of the “derivability conditions,” DC(i) to DC(iii) below, of [HBGM, p. 285], [F60, Theorem 4.7], or [L55]. Thus it must contain, at least, mathematical induction for formulas whose prenex normal forms contain at most existential quantifiers. For convenience, U is assumed also to contain symbols for primitive recursive functions and relations, and their defining equations. One of these is used to form the standard provability predicate, Prov ˹A˺, “there exists a number which is the Gödel number of a proof of A.” Upper corners denote numerals for Gödel numbers for the enclosed sentences, and parentheses are often omitted in their presence.

This paper contains some results concerning the relation between the sentence A, and the sentence Prov ˹A˺ in the Lindenbaum Sentence Algebra (LSA) for U, the Boolean algebra induced by the pre-order relation A ≤ B ⇔ ⊦A → B. Half of the answer is provided by a theorem of Löb [L55], which states that ⊦Prov ˹A˺ → A ⇔ ⊦A. Hence, in the presence of DC(iii), below, it is never true that Prov ˹A˺ < A in the LSA. However, there is a large and interesting set of sentences, denoted here by Γ, for which A < Prov ⌜A⌝.

The study of partition relations for cardinal numbers introduced by Erdös and his school in the 1950's has, for the past several years, had a profound impact in logic. Unfortunately, quite early in their development, it was noticed by Rado [1] that the potentially most fruitful class of such relations, infinite exponent partition relations, were always in contradiction with the axiom of choice (AC). As a result, such relations were overlooked. This turned out to be a mistake; for, as has been noticed recently, a close study of infinite exponent partition relations is both interesting and rewarding. For example, there are weakened versions of such relations which are provable in ZF and which have valuable applications in recursion theory and set theory. In addition, the pure theory of these relations, like that of the axiom of determinateness, is fruitful as well as elegant. For more background here one should refer to [3].

At any rate, with a more detailed look at infinite exponent partition relations came a more refined version of Rado's original theorem. Specifically, Rado used the full axiom of choice to carefully construct partitions to violate any desired relation—a more sophisticated look at the actual theory of such relations indicated how one could put together some desired partitions using only well-ordered choice [3].

The distinction between well-ordered choice and full choice is by no means vacuous in this context. For Mathias has shown [4] that the simplest infinite exponent partition relation, ω → (ω)ω, is consistent with countable choice (well-ordered choice of length ℵ0) and, in fact, is consistent with dependent choice.

It has long been known that every free associative algebra can be embedded in a skew field [11]; in fact there are many different embeddings, all obtainable by specialization from the ‘universal field of fractions’ of the free algebra (cf. [5, Chapter 7]). This makes it reasonable to call the latter the free field; see §2 for precise definitions. The existence of this free field was first established by Amitsur [1], but his proof is rather indirect and does not provide anything like a normal form for the elements of the field. Actually one cannot expect to find such a normal form, since it does not even exist in the field of fractions of a commutative integral domain, but at least one can raise the word problem for free fields: Does there exist an algorithm for deciding whether a given expression for an element of the free field represents zero?

Now some recent work has revealed a more direct way of constructing free fields ([4], [5], [6]), and it is the object of this note to show how this method can be used to solve the word problem for free fields over infinite ground fields. In this connexion it is of interest to note that A. Macintyre [9] has shown that the word problem for skew fields is recursively unsolvable. Of course, every finitely generated commutative field has a solvable word problem (see e.g. [12]).

The construction of universal fields of fractions in terms of full matrices is briefly recalled in §2, and it is shown quite generally for a ring R with a field of fractions inverting all full matrices, that if the set of full matrices over R is recursive, then the universal field has a solvable word problem. This holds more generally if the precise set of matrices over R inverted over the field is recursive, but it seems difficult to exploit this more general statement.

Let ZF be the usual Zermelo-Fraenkel set theory formulated without identity, and with the collection axiom scheme. Let ZF−-extensionality be obtained from ZF by using intuitionistic logic instead of classical logic, and dropping the axiom of extensionality. We give a syntactic transformation of ZF into ZF−-extensionality.

Let CPC, HPC respectively be classical, intuitionistic predicate calculus without identity, whose only homological symbol is ∈. We use the ~ ~-translation, a basic tool in the metatheory of intuitionistic systems, which is defined by

The two fundamental lemmas about this ~ ~ -translation we will use are

For proofs, see Kleene [3, Lemma 43a, Theorem 60d].

This - would provide the desired syntactic transformation at least for ZF into ZF− with extensionality, if A− were provable in ZF− for each axiom A of ZF. Unfortunately, the ~ ~-translations of extensionality and power set appear not to be provable in ZF−. We therefore form an auxiliary classical theory S which has no extensionality and has a weakened power set axiom, and show in §2 that the ~ ~-translation of each axiom of Sis provable in ZF−-extensionality. §1 is devoted to the translation of ZF in S.