1. The problem. The aim of the following considerations is to introduce a new type of non-Aristotelian logic by generalizing the truth-table methods so far employed for establishing non-Aristotelian sentential calculi. We shall expound the intended generalization by applying it to the particular set of pluri-valued systems introduced by J. Łukasiewicz. One will remark that the points of view illustrated by this example may serve to generalize quite analogously any other plurivalued systems, such as those originated by E. L. Post, by H. Reichenbach, and by others.

2. J. Łukasiewicz's plurivalued systems of sentential logic. First of all, we consider briefly the structure of the Łukasiewicz systems themselves.

As to the symbolic notation in which to represent those systems, we make the following agreements: For representing the expressions of the (two- or plurivalued) calculus of sentences, we make use of the Principia mathematica symbolism; however, we employ brackets instead of dots. We call the small italic letters “p”, “q”, “r”, … sentential variables or elementary sentences, and employ the term “sentence” as a general designation of both elementary sentences and the composites made up of elementary sentences and connective symbols (“~”, “ν” “.”, “⊃” “≡”).

Now, the different possible sentences (or, properly speaking, the different possible shapes of sentences, such as “p”, “p∨q”, “~p.(q∨ r)”, etc.) are the objects to which truth-values are ascribed; and just as in every other case one wants a designation for an object in order to be able to speak of it, we want now a system of designations for the sentences with which we are going to deal in our truth-table considerations.

1. The notion of derivability. Italic capitals, with or without subscripts, will be used as variables. They are to take as values some manner of elements which may for the present be left undetermined. Now let us consider abstractly the notion of the derivability of an element X from one or more specified elements by a series of steps of a specified kind. This involves reference to two conditions upon elements. One of these conditions, expressible by some statement form containing a single free variable, determines the elements from which X is said to be derivable. The other condition, expressed say by a statement form containing k + 1 free variables, determines the kind of steps by which the derivation is to proceed; it is the condition which any elements Z1, … Zk, Y must fulfill if progress from Zi, …, Zk to Y is to constitute a step of derivation in the intended sense. Supposing “f(Y)” supplanted by the first of these statement forms, whatever it may be, and “g(Z1, …, Zk, Y)” supplanted by the other, let us adopt the form of notation

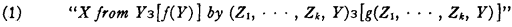
to express derivability of X in the suggested sense. The meaning of (1) can be formulated more accurately as follows:

(i) There are elements Y1 to Ym (for some m) such that Ym = X and, for each i≦m, either f(Yi) or else there are numbers j1 to Ym, each less than i, for which g(Yj1, …, Yjk, Yi).

(Variable subscripts are to be understood, here and throughout the paper, as referring only to positive integers.)

The notion (1) is illustrated in the ancestral R* of a relation R;1 for,

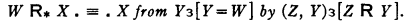
Another illustration is afforded by metamathematics. Suppose our elements are the expressions used in some formal system; suppose we have defined “Post(Y)”, meaning that Y is a postulate of that system; and suppose we have defined “Inf(ZI, …, Zk, Y)” (for some fixed k large enough for all purposes of the system in question), meaning that Y proceeds from Z1, …, Zk by one application of one or another of the rules of inference of the system. Then

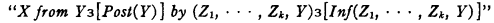
would mean that X is a theorem of the system.

Among various unnatural and technically burdensome effects of the theory of types, one is the unstable character of meaningfulness: a mere permutation of variables is capable of reducing a significant context to meaninglessness. Another effect, and perhaps the most conspicuous, is the systematic reduplication to which the logical constants are subjected; the calculi of classes and relations and even arithmetic lose their unity and generality, and are reproduced anew within each type. The elaborate compensatory manoeuvres which are thus made necessary are familiar to all readers of Principle, mathematica.

In a recent publication, to be cited henceforth as New foundations, I proposed an alternative course which avoids these consequences, but which would seem to offer less assurance of consistency. My efforts to derive a contradiction have delivered none, but they have lent a strange aspect to Cantor's proof that every class has more subclasses than members. This result is the topic of the present paper.

Preparatory to sketching the new system, which I shall call S′, I shall sketch a very similar but contradictory system S. By way of primitives S involves just membership, universal quantification, and alternative denial (Sheffer's stroke function), together with general variables “x”, “y”, …; the adequacy of this equipment as a basis for mathematical logic is made evident by Wiener's and Kuratowski's discovery of methods of constructing relation theory in terms of classes. Thus the formulae or statements and statement forms of S are describable recursively as follows: if a variable is put in each blank of “(ϵ)”, the result is a formula; if a variable enclosed in parentheses is prefixed to a formula, the result is a formula; and if a formula is put in each blank of “(∣)”, the result is a formula. The theorems of S are determined by a postulate and five rules, called P1 and R1-5 in New foundations. P1 and R1-3 specify various formulae as initial theorems, and R4-5 specify inferential connections for deriving further theorems. R1–2 and R4–5 are so fashioned as to provide the “theory of deduction”: they provide as theorems all those formulae which are valid by virtue merely of their structure in terms of alternative denial and quantification.

In this paper it will be shown that the fundamental modal functions (“… is necessary,” “… is possible,” etc.) may be represented in the ordinary two-valued logic of propositions, relatively to a subset S of the set K of all propositions of the logic. The only restriction on S is that no member of S can occur in any other member of S. The representation concerns the set SK consisting of all members of K in which occur members of S. Every member of SK may be regarded as a truth-function of the members of S. If S consists of only one member, P, and if f(P) and g(P) are any members of SK, then we define ∣f(P)∣ as (f(P)·f(~P)). The proposition “f(P) is S-necessary” may then be expressed by ∣f(P)· Furthermore we may express “f(P) is S-impossible” by ∣~f(P)∣, abbreviated to f(P)*; we may express “f(P) is S-possible” by abbreviated to f(P); and we may express “f(P) S-strictly implies g(P)” by (f(P)·~g(P))*, abbreviated to f(P)⊰g(P). Thus is obtained a novel analysis of modality, contrasting, on the one hand, with Carnap's syntactic theory of modality, and, on the other hand, with Lewis's view of modal concepts as underivable from other logical concepts. We would maintain that modal concepts are not absolute, but always relative to some S, generally unspecified.

In the formal exposition which follows, we shall assume tacitly but not explicitly the important distinction between the symbols we are discussing and symbols denoting or designating the former.

Introduction. In setting up his definition of analyticity, Carnap uses various non-constructive rules, of which we shall be concerned with only one. This one we shall call simply “Carnap's rule.” It can be roughly stated thus: If f(0), f(1), f(2), … are all provable, then (x)f(x) shall be provable.

In this paper will be briefly considered the logics got by starting with the system of Principia plus Peano's axioms and allowing one, two, …, ω, ω+l, and so on up to, but not including ω uses of Carnap's rule (interspersed with uses of the ordinary rules), as well as the system which includes Principia and Peano's axioms and is closed under application of Carnap's rule and the ordinary rules. Under suitable assumptions as to consistency, it is shown that in each of these logics there occur undecidable propositions and that a formula which states the consistency of the logic exists in the logic but is not provable in the logic. An interesting side result is that the logic got by allowing co applications of Carnap's rule is not closed under Carnap's rule.