We prove a theorem (1.7) about partial orders which can be viewed as a version of the Barwise compactness theorem which does not mention logic. The Barwise compactness theorem is easily equivalent to 1.7 + “Every Henkin set has a model”. We then make the observation that 1.7 gives us the definability of forcing for quantifier-free sentences in the forcing language and use this to give a direct proof of the truth and definability lemmas of forcing.

Contents: Introduction. §1: Computable rings and modules. §2: Ideal membership relation. §3: Effective structured domains. §4: Completion of a local ring as a domain. §5: The recursive completion. Epilogue. References.

Introduction. Completion is an important general mathematical device. Often, but not always, a completion takes the following form. Let A be a topological algebraic structure whose topology is derived from a metric. For A, a topological algebra  and an embedding i: A →  are constructed such that  is a complete metric space in which A is densely embedded by i. The long list of structures for which such completions exist begins with Cantor's construction of the real number field and includes objects like the p-adic integers, Baire space, and Boolean algebras. In Bourbaki [6] a careful and thorough account of completions for arbitrary topological groups and fields is given, for which it is important to note that the topological structures need not be metrizable, but must possess a uniformity.

The effectiveness of the completion process of a computable structure A cannot be readily studied using the tools of computable algebra, simply because the resulting structure  is almost invariably uncountable. However, in particular cases, it has been possible to define and study the substructure Ak of computable elements of Â; this has been done for the structures mentioned above, starting with the field of recursive real numbers.

In this paper we analyse the effectivity of the completion 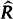of a local ring R. We do this using structured Scott-Ershov domains. Our study may be considered as a prototype containing methods applicable to a broad class of completions, including all the examples mentioned above, except for the real number field, which needs a generalisation of the domain concept.

A Scott-Ershov domain D formalises how a set Dt of possibly “infinite” elements, called total elements, is constructed from a set Dc of “finite” elements, called compact elements. This is achieved by means of an approximation ordering which determines a topology on D and, in particular, on Dt . Our methodology is to associate to a given topological algebra A a structured domain D(A) such that the total elements D(A)t form a topological algebra topologically isomorphic to A. In such circumstances A is said to be domain definable by D(A). The theory of computability for domains is now applied to study the effectivity of the topological algebra A.

The main result is Vaught's conjecture for weakly minimal, locally modular and non-ω-stable theories. The more general results yielding this are the following.

Theorem A. Suppose that T is a small unidimensional theory and D is a weakly minimal set, definable over the finite set B. Then for all finite A ⊂ D there are only finitely many nonalgebraic strong types over B realized in acl(A) ∩ D.

Theorem B. Suppose that T is a small, unidimensional, non-ω-stable theory such that the universe is weakly minimal and locally modular. Then for all finite A there is a finite B ⊂ cl(A) such that a ∈ cl(A) iff a ∈ cl(b) for some b ∈ B.

Recall the property (S) defined in the abstract of [B1].

Theorem C. Let T be as in Theorem B. Then, if T does not satisfy (S), T has many countable models.

Combining Theorem C and the results in [B1] we obtain Vaught's conjecture for such theories.

We prove that the only implications between four notions for Σ½-sets of reals are