1.1. In two previous papers a consistent theory of real numbers has been outlined by the author, using a system K′. This latter system is an extension of a system K, which is “basic” in the sense that every finitary (recursively enumerable) subclass of its well-formed expressions is in a certain sense represented in it. The system L described below is a further extension of K. The system K′ lacks two important features possessed by L: a symbol for a special kind of implication (or “conditionality”) and a symbol for the modal concept “necessity.” The presence of the implication symbol, and the additional assumptions that go with it, make available in L various kinds of restricted universal quantification not available in K′, for example, universal quantification restricted to the real numbers of the author's theory of real numbers.

1.2. If ‘~[a & ~a]’ is a theorem of L, then the proposition expressed by ‘a’ may be said to L-satisfy the principle of excluded middle. I t is always the case that ‘a’ L-satisfies the principle of excluded middle (or rather that the proposition expressed by ‘a’ does so) if and only if ‘a’ or ‘~a’ is a theorem of L. An example of a proposition that does not L-satisfy the principle of excluded middle is that expressed by ‘’, namely the proposition that asserts that the class of classes that are not members of themselves is a member of itself.

In this note we present a simplification of the axiom schemes which were given in our earlier paper Axiom schemes for m-valued propositional calculi. Except for new concepts that are needed for our present purposes, the terminology used will be the same as that introduced in the earlier paper. Hence, we can say that in addition to listing our simplified specifications for axiom schemes, we shall indicate how our new axiom schemes may be used to establish deductive completeness.

The simplification of our axiom schemes is achieved by using only the operators ⊃ and Jk( ) with the resulting elimination of ∨ and ·. This does not constitute an actual reduction in functional complexity since the latter operators can be denned in terms of the former. For example,

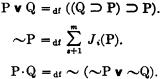
However, by dispensing with ∨ and · one can greatly reduce the number of axioms without an appreciable increase in the difficulties of proving deductive completeness.

Our simplified specifications for axiom schemes will retain conditions (1) and (3) of our earlier set but (2) and (4) will be changed to (2*) and (4*) which we will now state.

(2*) Assume that an implication function (P ⊃ Q) can be defined exclusively in terms of the basic functions Fi(P1, …:, Pαi).

The statement of what follows is simplified by introducing a chain symbol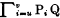 defined recursively as follows:

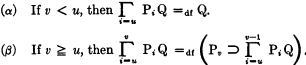
The variable i of a chain symbol which takes values from u to v will be called the chain variable. When it is clear that i is the chain variable we will use the notation 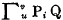in place of 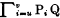. Hence, 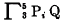denotes (P5 ⊃ (P4 ⊃ (P3 ⊃ Q))).

In this note two independent comments are offered concerning nominalistic syntax.

If one has a nominalistic theory of natural numbers (or positive integers) at one's disposal, one can of course readily formulate a nominalistic syntax by the familiar method of arithmetization. A nominalistic theory of natural numbers is formulated in a previous paper by the author, and thus a basis for a nominalistic syntax is already provided. (The objection that this theory is infinitistic would appear without force, because it provides the only known nominalistic basis for the theory of general recursive functions. On a finitistic basis one merely throws out this vital domain of mathematical theory.)

The second comment is concerned with nominalistic syntax as formulated by Goodman and Quine. The nominalistic construction of natural numbers alluded to above owes much of its power to a primitive device of ancestral quantification. This device is somewhat more powerful than the notions Goodman and Quine allow themselves. Now nominalistic syntax in their somewhat narrower sense can be formulated by utilizing a relation akin to the relation L of the theory of ordered individuals developed elsewhere by the author. ‘L’ here is to designate the relation between inscriptions of being wholly to the left of.

The Goodman-Quine primitive ‘C’, designating a relation of concatenation, and their primitive ‘Part’ with its field confined to inscriptions, can be defined in terms of ‘L’. Thus:

.

(This definition is essentially that of ‘P’ in O.I.)

The present note suggests how the computation of complexity-values outlined in The logical simplicity of predicates may be so modified as to satisfy a more stringent requirement than was there imposed.

By the method of computation described in that article, a basis consisting of two two-place predicates has in general the value 6. Any such basis may be replaced by one four-place predicate that is self-complete with respect to two of its places and also with respect to the remaining two. Such a predicate has but one “joint,” and therefore a value of 5. The consolidation of the two predicates into one thus results in a basis having a lower complexity-value. This does not violate the cardinal rule laid down in that article for testing proposed ways of assigning complexity-values; for, conversely, a four-place predicate that is self-complete in the way described can always be replaced by two two-place prediates. The rule requires a four-place predicate of the kind described to have a higher value than two two-place predicates only if replacement of two two-place predicates by such a four-place predicate is always possible, while replacement of such a four-place predicate by two two-place predicates is not.

However, we might reasonably strengthen our cardinal rule for complexity-valuation by adding as a second requirement:

If each basis of kind A is always replaceable by some basis of kind B, and each basis of kind B is always replaceable by some basis of kind A, then a basis of kind A and a basis of kind B must, in the absence of contrary indications, have the same complexity-value.

The calculus generated by the addition of the postulate

to S2 will, after Miss Alban, be called “S6”, the calculus generated by the addition of the same postulate to S3, “S7”, and the calculus generated by the addition of the postulate

to S3, “S8”. No interesting interpretation of the calculi S6–8 is known, but they are of some indirect interest because of the connections between them and the five calculi S1–S5. Certain questions concerning them will be treated in the following. In §1 it will be shown that every method of decision for S7 can be turned into a method of decision for S3, and in §2 that the number of complete extensions of S3 is equal to the number of complete extensions of S7 plus one. In §3 it will be shown that McKinsey's method of decision for S2 and S4 can be modified so as to cover S6.

The letters “P”, “Q”, “R”, and “S” will be employed as syntactic variables denoting formulas. Logical expressions will sometimes be used as selfdenotative. “C” and “C” stand for arbitrary calculi. “C + P” is the calculus which is the result of adding to C as new postulates all formulas which can be derived from P by substitution. With “substitution” I mean the operation performed on propositional variables.