Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T16:25:54.486Z Has data issue: false hasContentIssue false
  • English
  • Français

VARIETIES OF LEFT RESTRICTION SEMIGROUPS

Part of: Semigroups

Published online by Cambridge University Press:  29 January 2018

PETER R. JONES
PETER R. JONES*
Affiliation:
Department of Mathematics, Statistics and Computer Science, Marquette University, Milwaukee, WI 53201, USA email peter.jones@mu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Left restriction semigroups are the unary semigroups that abstractly characterize semigroups of partial maps on a set, where the unary operation associates to a map the identity element on its domain. They may be defined by a simple set of identities and the author initiated a study of the lattice of varieties of such semigroups, in parallel with the study of the lattice of varieties of two-sided restriction semigroups. In this work we study the subvariety 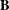$\mathbf{B}$ generated by Brandt semigroups and the subvarieties generated by the five-element Brandt inverse semigroup 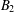$B_{2}$, its four-element restriction subsemigroup 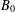$B_{0}$ and its three-element left restriction subsemigroup 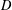$D$. These have already been studied in the ‘plain’ semigroup context, in the inverse semigroup context (in the first two instances) and in the two-sided restriction semigroup context (in all but the last instance). The author has previously shown that in the last of these contexts, the behavior is pathological: ‘almost all’ finite restriction semigroups are inherently nonfinitely based. Here we show that this is not the case for left restriction semigroups, by exhibiting identities for the above varieties and for their joins with monoids (the analog of groups in this context). We do so by structural means involving subdirect decompositions into certain primitive semigroups. We also show that each identity has a simple structural interpretation.

Keywords

left restriction semigroupweakly left E-ample semigroupvarietyidentityfinitely based

MSC classification

Primary: 20M07: Varieties and pseudovarieties of semigroups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 105 , Issue 2 , October 2018 , pp. 173 - 200
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Burris, S. and Sankappanavar, H. P., A Course in Universal Algebra (Springer, Berlin, 1981).Google Scholar
Gould, V. A. R., Notes on restriction semigroups and related structures (unpublished notes, available at www-users.york.ac.uk/∼varg1/restriction.pdf).Google Scholar
Gould, V. A. R. and Hollings, C., ‘Restriction semigroups and inductive constellations’, Comm. Algebra 38 (2010), 261–287.Google Scholar
Hollings, C., ‘From right PP monoids to restriction semigroups: a survey’, Eur. J. Pure Appl. Math. 2 (2009), 21–57.Google Scholar
Howie, J. M., Fundamentals of Semigroup Theory, London Mathematical Society Monographs (Clarendon Press, Oxford, 1995).Google Scholar
Jones, P. R., ‘On lattices of varieties of restriction semigroups’, Semigroup Forum 86 (2013), 337–361.Google Scholar
Jones, P. R., ‘The semigroups B 2 and B 0 are inherently nonfinitely based, as restriction semigroups’, Int. J. Algebra Comput. 23 (2013), 1289–1335.Google Scholar
Jones, P. R., ‘Varieties of restriction semigroups and varieties of categories’, Comm. Algebra 45 (2017), 1037–1056.Google Scholar
Jones, P. R., ‘The lattice of varieties of strict left restriction semigroups’, J. Aust. Math. Soc. to appear.Google Scholar
Kilp, M., Knauer, U. and Mikhalev, A., Monoids, Acts and Categories, De Gruyter Expositions in Mathematics, 29 (De Gruyter, Berlin, 2000).Google Scholar
Lee, E. W. H., ‘Subvarieties of the variety generated by the five-element Brandt semigroup’, Int. J. Algebra Comput. 16 (2006), 417–441.Google Scholar
Petrich, M., Inverse Semigroups (Wiley, New York, 1984).Google Scholar
Tilson, B., ‘Categories as algebra: an essential ingredient in the theory of monoids’, J. Pure Appl. Algebra 48 (1987), 83–198.Google Scholar
Trahtman, A. N., ‘Finiteness of identity bases of five-element semigroups’, in: Semigroups and Their Homomorphisms (ed. Lyapin, E. S.) (Leningrad State Pedagogical Institute, Leningrad, 1991), 76–97 (in Russian).Google Scholar