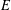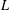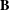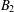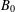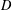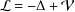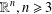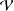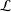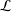In this paper we follow the approach of Bertrand–Beukers (and of Bertrand’s later work), based on differential Galois theory, to prove a very general version of Shidlovsky’s lemma that applies to Padé-approximation problems at several points, both at functional and numerical levels (that is, before and after evaluating at a specific point). This allows us to obtain a new proof of the Ball–Rivoal theorem on irrationality of infinitely many values of the Riemann zeta function at odd integers, inspired by the proof of the Siegel–Shidlovsky theorem on values of $E$-functions: Shidlovsky’s lemma is used to replace Nesterenko’s linear independence criterion with Siegel’s, so that no lower bound is needed on the linear forms in zeta values. The same strategy provides a new proof, and a refinement, of Nishimoto’s theorem on values of $L$-functions of Dirichlet characters.

Left restriction semigroups are the unary semigroups that abstractly characterize semigroups of partial maps on a set, where the unary operation associates to a map the identity element on its domain. They may be defined by a simple set of identities and the author initiated a study of the lattice of varieties of such semigroups, in parallel with the study of the lattice of varieties of two-sided restriction semigroups. In this work we study the subvariety $\mathbf{B}$ generated by Brandt semigroups and the subvarieties generated by the five-element Brandt inverse semigroup $B_{2}$, its four-element restriction subsemigroup $B_{0}$ and its three-element left restriction subsemigroup $D$. These have already been studied in the ‘plain’ semigroup context, in the inverse semigroup context (in the first two instances) and in the two-sided restriction semigroup context (in all but the last instance). The author has previously shown that in the last of these contexts, the behavior is pathological: ‘almost all’ finite restriction semigroups are inherently nonfinitely based. Here we show that this is not the case for left restriction semigroups, by exhibiting identities for the above varieties and for their joins with monoids (the analog of groups in this context). We do so by structural means involving subdirect decompositions into certain primitive semigroups. We also show that each identity has a simple structural interpretation.

Let ${\mathcal{L}}=-\unicode[STIX]{x1D6E5}+{\mathcal{V}}$ be a Schrödinger operator on $\mathbb{R}^{n},n\geq 3$, where ${\mathcal{V}}$ is a potential satisfying an appropriate reverse Hölder inequality. In this paper, we prove the boundedness of the Riesz transforms and the Littlewood–Paley square function associated with Schrödinger operators ${\mathcal{L}}$ in some new function spaces, such as new weighted Bounded Mean Oscillation (BMO) and weighted Lipschitz spaces, associated with ${\mathcal{L}}$. Our results extend certain well-known results.

We obtain a complete structural characterization of Cohn–Leavitt algebras over no-exit objects as graded involutive algebras. Corollaries of this result include graph-theoretic conditions characterizing when a Leavitt path algebra is a directed union of (graded) matricial algebras over the underlying field and over the algebra of Laurent polynomials and when the monoid of isomorphism classes of finitely generated projective modules is atomic and cancelative. We introduce the nonunital generalizations of graded analogs of noetherian and artinian rings, graded locally noetherian and graded locally artinian rings, and characterize graded locally noetherian and graded locally artinian Leavitt path algebras without any restriction on the cardinality of the graph. As a consequence, we relax the assumptions of the Abrams–Aranda–Perera–Siles characterization of locally noetherian and locally artinian Leavitt path algebras.

As generalizations of inverse semigroups, Ehresmann semigroups are introduced by Lawson and investigated by many authors extensively in the literature. In particular, Lawson has proved that the category of Ehresmann semigroups and admissible morphisms is isomorphic to the category of Ehresmann categories and strongly ordered functors, which generalizes the well-known Ehresmann–Schein–Nambooripad (ESN) theorem for inverse semigroups. From a varietal perspective, Ehresmann semigroups are derived from reducts of inverse semigroups. In this paper, inspired by the approach of Jones [‘A common framework for restriction semigroups and regular $\ast$-semigroups’, J. Pure Appl. Algebra216 (2012), 618–632], Ehresmann semigroups are extended from a varietal perspective to pseudo-Ehresmann semigroups derived instead from reducts of regular semigroups with a multiplicative inverse transversal. Furthermore, motivated by the method used by Gould and Wang [‘Beyond orthodox semigroups’, J. Algebra368 (2012), 209–230], we introduce the notion of inductive pseudocategories over admissible quadruples by which pseudo-Ehresmann semigroups are described. More precisely, we show that the category of pseudo-Ehresmann semigroups and (2,1,1,1)-morphisms is isomorphic to the category of inductive pseudocategories over admissible quadruples and pseudofunctors. Our work not only generalizes the result of Lawson for Ehresmann semigroups but also produces a new approach to characterize regular semigroups with a multiplicative inverse transversal.