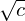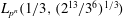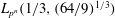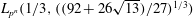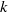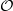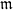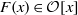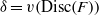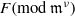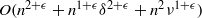Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 20
Weak Convergence of the Euler Scheme for Stochastic Differential Delay Equations
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 60-99
-
- Article
-
- You have access
- Export citation
- Cited by 20
Computations with classical and p-adic modular forms
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2011, pp. 214-231
-
- Article
-
- You have access
- Export citation
- Cited by 19
Constructing representations of Hecke algebras for complex reflection groups
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2010, pp. 426-450
-
- Article
-
- You have access
- Export citation
- Cited by 19
Primes in Elliptic Divisibility Sequences
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 1-13
-
- Article
-
- You have access
- Export citation
- Cited by 19
Computing with Nilpotent Orbits in Simple Lie Algebras of Exceptional Type
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 280-297
-
- Article
-
- You have access
- Export citation
- Cited by 19
A computational iterative method for solving nonlinear ordinary differential equations
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2015, pp. 730-753
-
- Article
-
- You have access
- Export citation
- Cited by 18
Almost sure asymptotic stability analysis of the θ-Maruyama method applied to a test system with stabilising and destabilising stochastic perturbations
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2012, pp. 71-83
-
- Article
-
- You have access
- Export citation
- Cited by 18
On a Result of Darboux
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 197-210
-
- Article
-
- You have access
- Export citation
- Cited by 18
Finite basis problem for semigroups of order six
- Part of:
-
- Published online by Cambridge University Press:
- 01 January 2015, pp. 1-129
-
- Article
-
- You have access
- Export citation
- Cited by 18
Computation on elliptic curves with complex multiplication
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2014, pp. 509-535
-
- Article
-
- You have access
- Export citation
- Cited by 17
Accelerating the CM method
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2012, pp. 172-204
-
- Article
-
- You have access
- Export citation
- Cited by 17
A generalized scheme based on shifted Jacobi polynomials for numerical simulation of coupled systems of multi-term fractional-order partial differential equations
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2017, pp. 11-29
-
- Article
-
- You have access
- Export citation
- Cited by 17
Reduced memory meet-in-the-middle attackagainst the NTRU private key
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2016, pp. 43-57
-
- Article
-
- You have access
- Export citation
- Cited by 17
The multiple number field sieve for medium- and high-characteristic finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 230-246
-
- Article
-
- You have access
- Export citation
- Cited by 17
Complexity of OM factorizations of polynomials over local fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2013, pp. 139-171
-
- Article
-
- You have access
- Export citation
- Cited by 17
Character Table of a Borel Subgroup of the Ree Groups 2F4(q2)
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 1-53
-
- Article
-
- You have access
- Export citation
- Cited by 17
On the use of expansion series for stream ciphers
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2012, pp. 326-340
-
- Article
-
- You have access
- Export citation
- Cited by 16
Resolving the Multitude of Microscale Interactions Accurately Models Stochastic Partial Differential Equations
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 193-221
-
- Article
-
- You have access
- Export citation
- Cited by 16
Efficient implementation of the Hardy–Ramanujan–Rademacher formula
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2012, pp. 341-359
-
- Article
-
- You have access
- Export citation
- Cited by 16
Computation of Galois groups of rational polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2014, pp. 141-158
-
- Article
-
- You have access
- Export citation