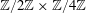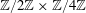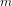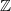Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 16
Parametrizing the moduli space of curves and applications to smooth plane quartics over finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 128-147
-
- Article
-
- You have access
- Export citation
- Cited by 16
Hyper-and-elliptic-curve cryptography
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2014, pp. 181-202
-
- Article
-
- You have access
- Export citation
- Cited by 16
Analysis of the GHS Weil Descent Attack on the ECDLP over Characteristic Two Finite Fields of Composite Degree
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 127-174
-
- Article
-
- You have access
- Export citation
- Cited by 16
Constructing genus-3 hyperelliptic Jacobians with CM
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2016, pp. 283-300
-
- Article
-
- You have access
- Export citation
- Cited by 15
A Recursive Method for Computing Zeta Functions of Varieties
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 222-269
-
- Article
-
- You have access
- Export citation
- Cited by 15
The Brauer-Manin Obstruction and III[2]
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 354-377
-
- Article
-
- You have access
- Export citation
- Cited by 15
A New Geometric Algorithm to Generate Smooth Interpolating Curves on Riemannian Manifolds
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 251-266
-
- Article
-
- You have access
- Export citation
- Cited by 15
Computing the Rank of Elliptic Curves over Number Fields
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 7-17
-
- Article
-
- You have access
- Export citation
- Cited by 15
High-rank elliptic curves with torsion
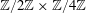 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}$ induced by Diophantine triples
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/4\mathbb{Z}$ induced by Diophantine triples
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2014, pp. 282-288
-
- Article
-
- You have access
- Export citation
- Cited by 15
PyCox: computing with (finite) Coxeter groups and Iwahori–Hecke algebras
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2012, pp. 231-256
-
- Article
-
- You have access
- Export citation
- Cited by 15
The Relative Consistency of the Axiom of Choice Mechanized Using Isabelle⁄zf
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 198-248
-
- Article
-
- You have access
- Export citation
- Cited by 14
Fast Constructive Recognition of Black-Box Unitary Groups
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 162-197
-
- Article
-
- You have access
- Export citation
- Cited by 14
Eigenvalue enclosures and exclosures for non-self-adjoint problems in hydrodynamics
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2010, pp. 65-81
-
- Article
-
- You have access
- Export citation
- Cited by 14
On the combinatorial classification of toric log del Pezzo surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 01 January 2010, pp. 33-46
-
- Article
-
- You have access
- Export citation
- Cited by 14
Torsion Units in Integral Group Ring of the Mathieu Simple Group M22
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 28-39
-
- Article
-
- You have access
- Export citation
- Cited by 14
A Domain-Theoretic Account of Picard's Theorem
-
- Published online by Cambridge University Press:
- 01 February 2010, pp. 83-118
-
- Article
-
- You have access
- Export citation
- Cited by 14
Computing functions on Jacobians and their quotients
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2015, pp. 555-577
-
- Article
-
- You have access
- Export citation
- Cited by 14
Squarefree values of trinomial discriminants
- Part of:
-
- Published online by Cambridge University Press:
- 01 January 2015, pp. 148-169
-
- Article
-
- You have access
- Export citation
- Cited by 13
On level one cuspidal Bianchi modular forms
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2013, pp. 187-199
-
- Article
-
- You have access
- Export citation
- Cited by 13
Single-class genera of positive integral lattices
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2013, pp. 172-186
-
- Article
-
- You have access
- Export citation